Вопрос 2. Свободные затухающие электромагнитные колебания. Дифференциальное уравнение свободных затухающих колебаний и его решение

Поскольку всякий реальный контур обладает активным сопротивлением R ≠ 0, это приводит к затуханию колебаний. Введем обозначение β = R /2 L, где β – коэффициент затухания, тогда уравнение (2.3) можно переписать следующим образом

d ² q/dt ² + 2βdq/dt + ω₀ ² q = 0. (2.9)

(2.9) – дифференциальное уравнение свободных затухающих колебаний.

При условии, что β<ω ₀ решение уравнения (2.9) для заряда q имеет вид затухающих колебаний:

q = q_m e^{- βt} cos(ωt + α), (2.10)

где − частота затухающих свободных колебаний, очевидно, что ω<ω₀. Таким образом, потери энергии в контуре приводят к изменению не только амплитуды колебаний, но и их частоты.

После подстановки в последнее выражение значений для ω₀ и β, получим

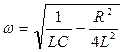. (2.11)

При R = 0 выражение (2.11) переходит в (2.4).

Колебания заряда на обкладках конденсатора с периодом Т = 2π / ω и убывающей амплитудой 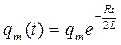и колебания силы тока в контуре представлены на рис.2.3, на котором показано затухание свободных колебаний в RLC - контуре.

Характерное время затухания электрических колебаний в контуре определяется временем релаксации

τ = 1/ β = 2L / R,

t

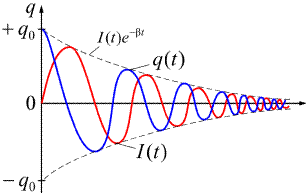
Рис.2.3

т.е. индуктивность L является мерой инертности для электрических колебаний заряда, а значит, и силы тока в контуре.

Напряжение на конденсаторе пропорционально заряду q, поэтому оно изменяется синхронно с зарядом q, а сила тока в контуре

I = dq / dt = q_m e^{- βt}[ -βcos (ωt + α) – ωsin (ωt + α)].

Это выражение можно преобразовать к виду

I = I _me ^-βtcos (ωt + α + Δ). (2.12)

Из (2.12) видно, что сила тока в контуре затухает со временем, а колебания тока происходят с некоторым опережением по фазе (Δ) относительно колебания заряда (напряжения) на конденсаторе.

Затухающие колебания представляют собой, вообще говоря, непериодические колебания, так как в этом случае не повторяются максимальные значения заряда, силы тока и напряжения. Однако если затухание мало, можно условно пользоваться понятием периода как промежутка времени между, например, двумя последовательными максимумами (минимумами) колеблющейся физической величины.

Тогда период затухающих колебаний определяется выражением:

,

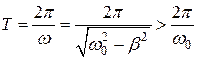т.е. 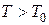. Здесь величины и 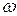называют условным периодом и условной циклической частотой затухающих колебаний. Из формулы следует, что с ростом коэффициента затухания период колебаний увеличивается. При β = ω ₀ период колебаний обращается в бесконечность, т.е. движение перестает быть периодическим. При β > ω ₀ движение носит апериодический (непериодический) характер, т.е. выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

Затухание колебаний принято характеризовать логарифмическим декрементом затухания

λ = ln a (t)/ a (t + T) = βT, (2.13)

где a (t) – амплитуда соответствующей величины (q, U или I). Вспомним, что λ = 1/ N _e, где N _e- число колебаний, совершаемых за время, в течение которого амплитуда уменьшается в е раз.

Подставив в (13) значение для β = R /2 L и Т =2π/ ω, получим

λ = (R /2 L)(2π/ ω) = π R / Lω, (2.14)

т.е. логарифмический декремент затухания определяется параметрами контура L, C и R и является характеристикой контура.

Если затухание невелико (β << ω ₀), то в (2.14) можно считать ω ≈ ω ₀ =

1/ 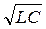. Тогда

λ ≈ (π R / L)· 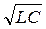= π R .

Величину , которая имеет размерность электрического сопротивления, называют волновым сопротивлением R _волн, т.е. R _волн = .

Качество колебательного контура часто характеризуют его добротностью Q, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания

Q = π/ λ = π N _e.(2.15)

Видно, что добротность контура тем больше, чем большее число колебаний он успевает совершить, прежде чем амплитуда колебаний уменьшиться в е раз. В случае слабого затухания

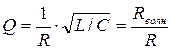. (2.16)

При увеличении сопротивления контура R затухание колебаний увеличивается, коэффициент затухания растет, а добротность контура уменьшается и при β ² ≥ ω ₀²вместо колебаний в контуре происходит апериодический разряд конденсатора (рис. 2.4).

Сопротивление контура, при котором колебательный процесс

Рис. 2.4

переходит в апериодический, называется критическим. Значение критического сопротивления R _k определяется условием

R _k²/4 L ² = 1/ LC, (2.17)

откуда

R _k = 2 = 2 R _волн. (2.18)

Таким образом, условие возможности колебаний в контуре записывается в виде:

R < 2 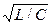= R _k. (2.19)

Дата добавления: 2014-11-06