Вопрос 3. Анализ поляризованного света

Рассмотрим нормальное падение поляризованного света на поверхность пластинки, вырезанной параллельно оптической оси Y (рис.13.3).

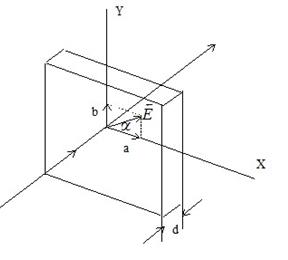
Рис. 13.3

Падающий на пластинку свет представим как совокупность двух волн, поляризованных вдоль оптической оси и перпендикулярно к ней. Первая из этих волн необыкновенная, вторая – обыкновенная. В пластинке обе волны распространяются в одном направлении, но с различными скоростями. Пройдя через пластинку толщиной d, волны приобретут дополнительную разность хода d⋅ (n_o — n_e), где n_o и n_e – показатели преломления обыкновенного и необыкновенного лучей соответственно. Тогда на выходе из пластинки разность фаз между двумя рассматриваемыми волнами будет равна 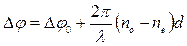. (13.1)

Здесь λ – длина волны; 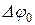- разность фаз между обыкновенным и необыкновенным лучами в момент падения на пластинку.

После выхода из пластинки обыкновенный и необыкновенный лучи, складываясь, дают в общем случае свет эллиптической поляризации. Рассмотрим этот вопрос подробнее.

Для упрощения предположим, что 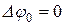. Обозначим амплитуду колебаний обыкновенного луча через a, а необыкновенного – через b (рис.13.3).

Тогда колебания обыкновенного и необыкновенного лучей могут быть представлены в виде:

, (13.2)

, (13.3)

где ω – циклическая частота электромагнитной волны, а Δ φ – разность фаз, возникающая между лучами при прохождении ими кристаллической пластинки.

Выразим из (13.2) :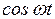

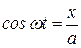. (13.4)

Перепишем (13.3) в виде:

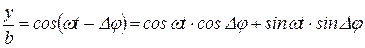. (13.5)

С учётом (13.4) равенство (13.5) примет вид:

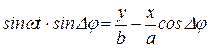. (13.6)

Запишем равенство:

. (13.7)

Возведём в квадрат левые и правые части равенств (13.6) и (13.7) и почленно просуммируем:

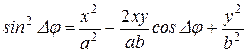(13.8)

Как следует из (13.8), при прохождении через кристаллическую пластинку линейно поляризованный свет становится, в общем случае, эллиптически поляризованным. Ориентация осей эллипса и соотношение между ними будут зависеть от поляризации падающего на пластинку света, толщины и ориентации пластинки.

Для получения и анализа поляризованного света, как правило, используют поляризаторы в сочетании с кристаллическими пластинками, вырезанными параллельно оптической оси.

Выше отмечалось, что при прохождении линейно поляризованного света через кристаллическую пластинку его поляризация, в общем случае, становится эллиптической.

Рассмотрим некоторые частные случаи.

Пусть разность хода, создаваемая пластинкой между обыкновенным и необыкновенным лучами, удовлетворяет условию

(13.9)

Такая пластинка называется пластинкой в четверти длины волны (пластинка в ). Из формулы

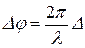, (13.10)

описывающей взаимосвязь между разностью фаз и разностью хода, следует, что на выходе из пластинки в четверть длины волны разность фаз равна

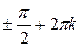. Подставив это значение разности фаз в формулу (13.8), получаем уравнение

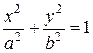. (13.11)

Следовательно, после прохождения пластинки в линейно поляризованный свет становится эллиптически поляризованным. Однако, если оси пластинки расположены так, что угол 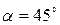(рис. 1), то амплитуды колебаний векторов обыкновенного и необыкновенного лучей будут равны (a = b), а на выходе из пластинки свет окажется поляризованным по кругу. При этом положительное значение разности фаз соответствует поляризации по левому кругу, а отрицательное – по правому. При a = b получаем уравнение окружности:

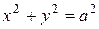. (13.12)

Для пластинки в половину длины волны разность хода равна

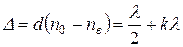, 13.13)

где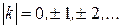

Этой разнице хода соответствует разность фаз

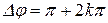. (13.14)

Подстановка данного выражения в (13.8) приводит к уравнению

. (13.15)

Следовательно, выходящий из полудлинноволновой пластинки свет остаётся линейно поляризованным, но плоскость колебаний вектора зеркально симметрично отражается относительно осей пластинки (рис. 13.3). На рис. 13.3 изображено направление колебаний вектора до (13.1) и после (13.2) пластинки.

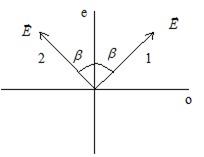
Рис. 13.4

Для пластинки в целую длину волны разность хода равна:

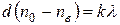, (13.16)

где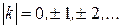

Учитывая, что в этом случае разность фаз между обыкновенным и необыкновенным лучами составляет 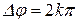, получаем после подстановки в (13.8) уравнение, описывающее поляризацию излучения,

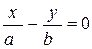. (13.17)

Это означает, что при прохождении света через пластинку в целую длину волны, он остается линейно поляризованным, причем не изменяет направление плоскости колебаний.

Таким образом, анализ поляризованного света производится с помощью поляризаторов и кристаллических пластинок. Этот процесс можно разделить на два этапа.

На первом этапе анализ производится только с помощью одного поляризатора. Если при вращении поляризатора интенсивность света будет изменяться от некоторого максимального значения до нуля, то это означает, что падающий на поляризатор свет является линейно поляризованным.

Если при повороте поляризатора интенсивность проходящего через него света остается неизменной, то свет может быть либо естественным, либо светом круговой поляризации.

Если же при повороте поляризатора интенсивность света изменяется от некоторого максимального до минимального, не равного нулю, значения, то падающий на поляризатор свет имеет эллиптическую поляризацию или является светом частично поляризованным.

Для того, чтобы отличить свет круговой поляризации от естественного и свет, поляризованный по эллипсу, от частично поляризованного света (являющегося смесью света линейно поляризованного с естественным), применяется оптическая система: пластинка в четверть волны – поляризатор.

При прохождении света круговой поляризации через пластинку между обыкновенным и необыкновенным лучами появляется дополнительная разность фаз в 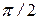. Это приводит к тому, что на выходе из пластинки свет становится линейно поляризованным. Свет естественный после прохождения четвертьволновой пластинки остаётся естественным, изменяя свою внутреннюю структуру, т. е. вместо совокупности хаотически расположенных относительно оси распространения линейных осцилляторов будет наблюдаться совокупность эллипсов с хаотическим расположением их осей. С помощью расположенного за пластинкой поляризатора легко отличить линейно поляризованный свет от естественного.

Для того, чтобы различить свет эллиптической поляризации и частично поляризованный, необходимо с помощью поляризатора определить направление осей эллипса. Установив кристаллическую пластинку в таким образом, чтобы её оси составляли угол 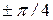. По направлению к большой оси эллипса, пропускают свет через данную пластинку. Свет, поляризованный эллиптически, пройдя через пластинку и получив дополнительную разность фаз в 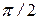, останется эллиптически поляризованным, изменив при этом ориентацию осей эллипса. При прохождении через четвертьволновую пластинку частично поляризованного света его составляющая, имеющая линейную поляризацию, превратится в свет круговой поляризации, а естественная составляющая, как отмечалось выше, лишь изменит свою внутреннюю структуру. При пропускании такого излучения через поляризатор интенсивность прошедшего через него света не будет зависеть от угла поворота плоскости поляризатора.

Дата добавления: 2014-11-06