V. Неопределенный и определенный интегралы

Для справок приводим таблицу неопределенных интегралов. Интегрирование, основное на применение таблицы основных интегралов, основных свойств неопределенного ∫ - ла, а также простейших тождественных преобразований подынтегральной функции, принято называть непосредственным интегрированием.

1.

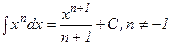
2.

3.

4.

5.

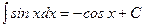
6.

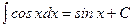
7.

8.

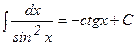
9.

10.

11.

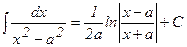
12.

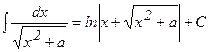
Пример 1. Найти интегралы:

а) б) в)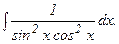

Решение.

а) Применяя табличные интегралы, получим:

.

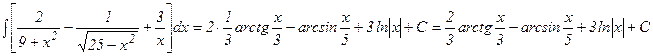б) Преобразуем подынтегральную функцию и представим заданный интеграл в виде суммы двух других, каждый из которых табличный:

в) Чтобы привести данный интеграл к табличному, выразим стоящую в числителе единицу как sin²x + cos²x и разделим почленно на знаменатель:

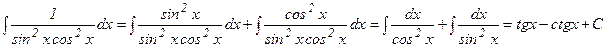
Если данный интеграл 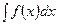не является табличным и не может быть найден способом непосредственно интегрирования, то введение новой переменной интегрирования позволяет свести данный интеграл к табличному. В этом сущность так называемого метода подстановки.

Пример 2. Найти интегралы, применяя соответствующие подставки:

а) б) в) .

Решение.

а) Чтобы привести данный интеграл к табличному, положим t = x² + 1. Дифференцируя, получим dt = 2xdx, xdx = . Производя замену, получаем:

б) Пусть t = arcsin x, тогда 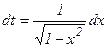; следовательно,

.

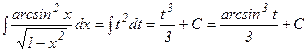в) Так как cosxdx есть дифференциал функции sin x, то данный интеграл приводится к табличному так:

Пусть u и – дифференцируемые функции от переменной х. Определим дифференциал произведения этих функций:

d (u ) = ud + du, откуда ud = d (u ) – du.

Проинтегрировав обе части последнего равенства, получим:

(1)

Эта формула (1) называется формулой интегрирования по частям. Ей пользуются в тех случаях, когда 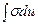есть более простой интеграл по отношению к данному интегралу .

Пример 3. Найти интегралы: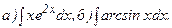

Решение.

а) Пусть u = х и dσ = e^2xdx, тогда du = dx и σ = .

Произвольную потоянную С можно учесть в окончательном ответе.

Применяя (1), получаем:

б) Пусть u = arc sin x, dσ = dx, тогда

+

Интегрирование рациональных дробей

Рациональной дробью называется дробь вида , где Р(х) и Q(х) – многочлены. Рациональная дробь называется правильной, если степень многочлена Р(х) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.

Простейшими (элементарными) дробями называются правильные дроби следующего вида:

I. II. 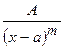, где m – целое число, m > 1;

III. 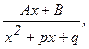где 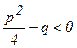, т.е. квадратный трехчлен х² + рх + q не имеет действительных корней;

IV. 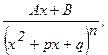где n – целое число, n > 1; т.е. квадратный трехчлен х² + рх + q не имеет действительных корней.

Во всех четырех случаях предполагается, что А, В, р, q, а – действительные числа. Перечисленные дроби соответственно называют соответственно дробями I, II, III и IV типов.

Рассмотрим интегралы от простейших дробей I, II, III типов:

I. .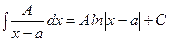

II. .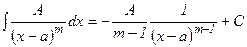

III. (здесь в знаменателе исходного интеграла выделили полный квадрат и свели к табличному интегралу).

IV. 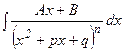- сводится к табличному либо путем различных преобразований подинтегральной функции, либо используя рекуррентную формулу.

Пример 4. Найти интегралы:

Решение.

а) Данная дробь – правильная, ее знаменатель разложен на простейшие множители. Множителю (х – 1)³ соответствует сумма трех простейших дробей 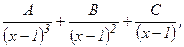а множителю (х + 3) – простейшая дробь Итак, имеем:

Освободимся от знаменателя:

х² + 1 = А(х + 3) + В(х – 1)²(х + 3) + С(х – 1)²(х+3)+ D(x – 1)³ (*)

Действительными корнями знаменателя являются числа 1 и –3.

Полагая в (*) х = 1, получаем, что 2 = 4А или А=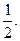

Полагая в (*) х = -3, получаем, что 10 = - 64 D или D = .

Сравним теперь коэффициенты при старших степенях х в левой и правой частях (*), т.е. при х³. В левой части равенства (*) нет члена с х³, т.е. коэффициент при х³ равен 0. В правой части коэффициент при х³ равен С + D. Итак, С + D = 0, откуда C =

Остается определить коэффициент В. Для этого надо иметь еще одно уравнение. Это уравнение можно получить путем сравнения коэффициентов при одинаковых степенях х (например, при х²) или придав х какое-нибудь числовое значение. Удобнее взять такое значение, при котором вычислений будет возможно меньше. Полагая х = 0, получаем из равенства (*): 1 = 3А – 3В + 3С – D или 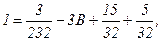т.е.

Окончательное разложение данной дроби на простейшие имеет вид:

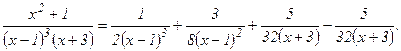
Таким образом, получим:

б) Разложим знаменатель дроби на множители: х⁵ – х² = х²(х³ - 1) = х²(х – 1) (х² + х + 1).

Тогда

Освобождаемся от знаменателя:

1 = А(х – 1)(х² +х + 1) + В(х – 1)(х² + х + 1)х + С х²(х² + х + + 1) + (Dx + E) x² (x – 1).

Действительными корнями знаменателя являются числа 0 и 1. Из последнего равенства при х = 0 имеем 1 = -А, т.е. А = -1; при х = 1, имеем 1 = 3С, т.е. С =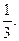

Перепишем предыдущее равенство в виде:

1 = А(х³ – 1) + В(х⁴ – х) + С(х⁴ + х³ + х²) + Dx⁴ +Ex³ –Dx³ – Ex².

Сравнивая коэффициенты при х⁴, х³, х², получаем систему уравнений

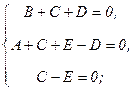
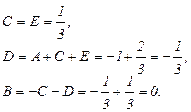
Итак,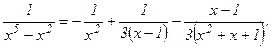

Следовательно,

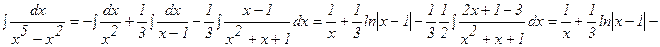
в) Так как х² + 1 есть двукратный множитель, то Освобождаясь от знаменателя, получаем: х³- 2х = Ах + В + (Сх + D) (х²+ 1). Приравниваем коэффициенты при одинаковых степенях х:

х³: 1 = С,

х²: 0 = D,

х: -2 = А + С, А = -3,

х⁰: 0 = В + D, В = 0.

Следовательно,

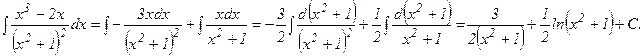
г) Выделим целую часть данной неправильной дроби, поделив числитель на знаменатель:

Следовательно,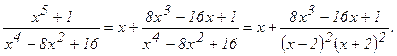

Разложим теперь правильную дробь на простейшие дроби:

Освободимся от знаменателей:

8х³ – 16х + 1 = А(х + 2)²+ В(х – 2)(х + 2)²+С(х – 2)²+D(х + 2)(х – 2)².

Принимая в последнем равенстве:

х = 2: 33 = 4² А, откуда А=

х = -2: -31 = 16 С, откуда С= -

х =0: 1 = 4А – 8В + 4С + 8D, откуда –16В + 16D = 1.

Для того, чтобы найти В и D, сравнив коэффициенты при х³, получим еще одно уравнение: 8 = В + D. Решим получившуюся систему уравнений:

Находим, что

Итак,

Пример 5. Вычислить приближенное значение определенного интеграла 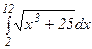с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Решение.

Приближенные методы интегрирования имеют очень большое значение. На практике часто приходится иметь дело с определенными интегралами, которые с помощью формулы Ньютона – Лейбница или искусственными приемами найти практически невозможно. В этом случае значение интеграла 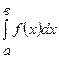находят приближенно, например, применяя формулу Симпсона:

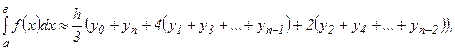(2)

где n – четное число, на которое разбивается отрезок интегрирования,

В данном примере n = 10, а = 2, в = 12, то

.

Составим таблицу значений данной функции :

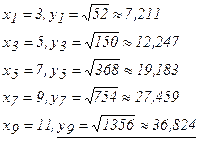
47,614

4

411,696

80,147

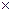
2

160,294.

Окончательно получаем: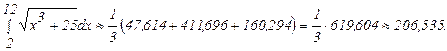

Несобственные интегралы

Несобственными интегралами называются:

1) интегралы с бесконечными пределами;

2) интегралы от неограниченных функций.

Несобственный интеграл от функции f(x) в пределах от а до + ∞ определяется равенством:

(3)

Если этот предел существует и конечен, то несобственный интеграл (3) называется сходящимся; если же предел не существует или равен бесконечности – расходящимся.

Аналогично:

(4)

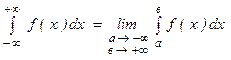(5)

Если функция f(x) имеет бесконечный разрыв в точке с отрезка [ a; в ] и непрерывна при а ≤ х <с и с < х ≤ в, то по определению полагают:

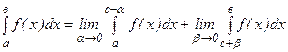(6)

Несобственный интеграл , где f(c) = ∞, a < c < в, называется сходящимся, если существуют оба предела в правой части равенства (6), и расходящимся, если не существует хотя бы один из них.

Пример 6. Вычислить несобственные интегралы или установить их расходимость:

а) б) в)

Решение.

а) Применяя равенство (3), получаем:

следовательно, рассматриваемый несобственный интеграл расходится.

б) Применяя равенство (4), получаем:

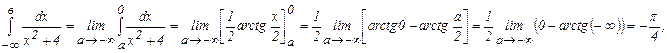следовательно, данный интеграл сходится и он равен .

в) Подынтегральная функция имеет бесконечный предел при х = 1, т.е. в точке, принадлежащей интервалу интегрирования.

Применяя равенство (6), получаем:

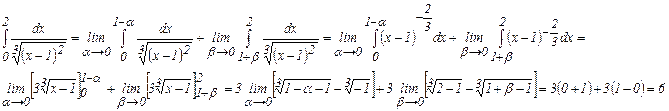
следовательно, данный интеграл сходится и он равен 6.

Дата добавления: 2014-11-06