Формула Тейлора

(1)

С ее помощью можно вычислить приближенные значения функции f(x), если известны значения этой функции и ее производных до порядка n в «начальной» точке x=a и если, кроме того, удается оценить остаточный член R_n. Если

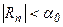, то (2)

(3)

с погрешностью α₀.

Для оценки погрешности формулы (3) чаще всего используется запись остаточного члена R_n в форме Лагранжа:

И

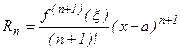, где ξ лежит между точками а и х. (4)

Пример 3. Применяя формулу Тейлора с остаточным членом в формуле Лагранжа, вычислить е^0,1 и е^0,2 с точностью 0,001.

Решение: Формула Тейлора с остаточным членом в форме Лагранжа для функции f(x)=e^x имеет вид:

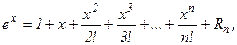где

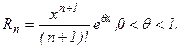Отсюда получим:

Значения х₁ = 0,1 и х₂ = 0,2 принадлежат отрезку [0;½],следовательно, 0<θx<0,5 и е ^θx<e^0.5<2;

Требуется определить n так, чтобы выполнялось неравенство R_n<0,001 и х = 0,1.

Положим х = 0,1 и вычислим несколько первых членов разложения, сравнивая их с заданной точностью α = 0,001:

u₀=1=1,0000>α,

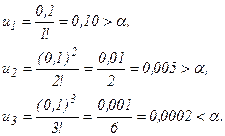
Итак, для вычисления е^0,1 с α =0,001 достаточно взять первые 4 слагаемых.

е^0,1≈1+0,1+0,005+0,0002≈1,1052≈1,105.

Полагая х=0,2 аналогично можно найти, что достаточно 5 слагаемых и е^0,2≈1,221.

Пример 4. Найти наибольшее и наименьшее значения функции у=3х-х³ на отрезке [-2;3].

Решение: Найдем производную: у' = 3-3х²=3(1-х²). Приравняв у' к нулю, находим стационарные точки: 3(1-х²)=0, т.е. х₁=1 и х₂=-1.

Определяем значения функции в этих точках:

f(1)=2,

f(-1)=-2.

Вычисляем значения данной функции на границах промежутка:

f(-2)=2,

f(3)=-18.

Из полученных четырех значений выбираем наибольшее и наименьшее. Итак, наибольшее значение функции на отрезке [-2;3] f_наиб = 2, а наименьшее f _наим = -18.

Пример 5. Исследовать методами дифференциального исчисления функцию 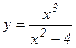и, используя результаты исследования, построить ее график.

Решение: Исследование функции проведем по следующей схеме:

1. Найдем область определения функции.

2. Исследуем функцию на четность и нечетность.

3. Найдем точки пересечения графика функции с осями координат.

4. Исследуем функцию на непрерывность; найдем точки разрыва (если они

существуют) и установим характер разрыва.

5. Найдем асимптоты кривой у = f(x).

6. Найдем интервалы возрастания и убывания функции и ее экстремумы.

7. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.

Реализуем данную схему.

1. Функция определена при всех значениях аргумента х, кроме х=±2, т.е. область определения функции D(y) = (-∞;-2)U(-2;2)U(2;+∞).

2. Для установления четности или нечетности функции проверим выполнимость равенств для любых х и –х из области определения функции:

a) Если f(-x) = f(x), тогда f(x) - функция четная, т. е. ее график симметричен относительно оси О у;

b) Если f(-x) = -f(x), тогда f(x) - функция нечетная, т. е. ее график симметричен относительно начала координат т. О(0;0).

Итак, , следовательно, данная функция является нечетной.

3. Для нахождения точек пересечения графика функции с осью Ох полагаем у=0; с осью О у — х=0.

х=0; у=0.

у=0,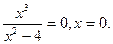

Т.е., график функции пересекает систему координат в т. О(0;0).

4. Данная функция является элементарной, поэтому она непрерывна на своей области определения D(у). Найдем односторонние пределы функции в указанных точках:

.

Т.о., в точках х=±2 функция имеет разрыв второго рода и прямых х = -2 и х = 2 – вертикальные асимптоты графика функции.

5. Найдем наклонные асимптоты у=kx+b, где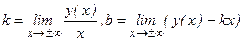

Т.о., наклонная асимптота имеет уравнение у = х.

6. Значение f(x₀) называется максимумом функции f(x), если при любом достаточно малом h>0 выполняются условия f(x₀-h)<f(x₀) и f(x₀+h)<f(x₀). Точка х₀ называется в этом случае точкой максимума функции f(x) (рис.5).

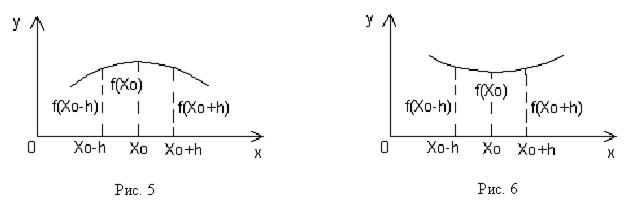
Значение f(x₀) называется минимумом функции f(x), если при любом достаточно малом h>0 выполняются условия f(x₀-h)>f(x₀) и f(x₀+h)>f(x₀). Точка х₀ называется в этом случае точкой минимума функции f(x) (рис. 6).

Максимум или минимум функции называется экстремумом функции.

Необходимое условие экстремума. Если функция f(x) в точке х₀ имеет экстремум, то производная f'(x₀) обращается в нуль или не существует.

Точка х₀, в которой f'(x₀)=0, называется стационарной точкой. Точки, в которых f'(x)=0 или f'(x) не существует, называются критическими точками. Не всякая критическая точка является точкой экстремума.

Функция f(x) называется возрастающей в интервале (a;b), если для любых двух точек х₁и х ₂ из указанного интервала, удовлетворяющих неравенству х₁< х ₂, выполняется неравенство f(x₁)<f(х₂). Если же f(x₁)>f(х₂) при х₁< х ₂, то функция f(x) называется убывающей в интервале (a;b).

Найдем производную данной функции

Найдем критические точки:

х₁=0; х²=12, х₂=

х₂= .

х²≠4, х≠±2 –не входят в область определения функции D(y), значит, экстремума в этих точках быть не может.

Разобьем числовую ось на 5 интервалов, составим таблицу и определим знак первой производной в каждом интервале.

х	-∞;-2	-2	-2 ;-2	-2;2	2; 2	2	2 ;+∞
у'(x)	+		-	-	-		+
у(x)	возрастает	-3	убывает	убывает	убывает	3	возрастает
		max				min

При переходе через точку х = -2 первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум: у_max = у (-2 )= -3 .

Значит, А (-2 ;-3 ) - точка максимума.

При переходе через точку х = -2 первая производная меняет свои знаки с минуса на плюс, поэтому в этой точке функция имеет минимум: у_min = у (2 )= 3 . Значит, В (2 ;3 ) - точка минимума.

7. Достаточное условие выпуклости (вогнутости) графика функции.

Если f''(x)<0 в интервале (a;b), то график функции является выпуклым в этом интервале; если же f''(x)>0, то в интервале (a;b) график функции - выпуклый.

График функции у=f(х) называется выпуклым в интервале (a;b), если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.7).

График функции называется вогнутым в интервале (a;b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис.8).

Точка (х₀;f(х₀)) графика функции, отделяющая его выпуклую и вогнутую части, называется точкой перегиба.

Найдем вторую производную:

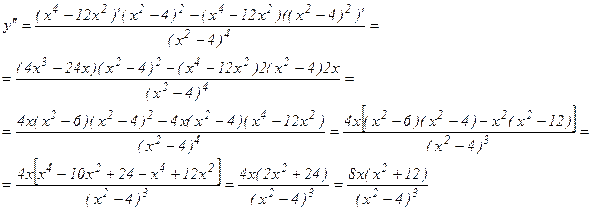
y''=0 при х=0 и y'' – не существует при х=±2; которые не входят в область определения функции.

Составим таблицу, разбив числовую ось на интервалы и определим знак второй производной в каждом из них:

х	-∞;-2	-2;0		0;2	2;+∞
y''(х)	-	+		-	+
у(х)	∩	U		∩	U

На интервалах (-∞;-2) и (0;2) y''<0 и дуга кривой выпукла; на интервалах (-2;0) и (2;+∞), y''>0 и тем самым график является вогнутым.

При переходе через точку х=0 y'' меняет свой знак, поэтому х=0 - абсцисса точки перегиба. Следовательно, С(0;0) – точка перегиба графика функции.

График исследуемой функции показан на рис.9.

Дополнительные точки для построения графика:

х	-3	-5	-1	-1,5
у	-5,4	-5,6		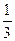-2

Дата добавления: 2014-11-06