
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Подставим в (3) данные векторы 1, 2, 3, 4 , получим
|
|
|
|
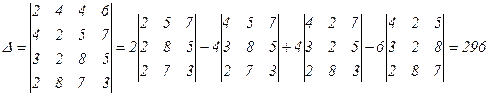
Так как 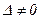 , то векторы линейно независимы и они образуют базис линейного пространства R4. Для вычисления координат вектора
, то векторы линейно независимы и они образуют базис линейного пространства R4. Для вычисления координат вектора  в этом базисе составим систему линейных уравнений из координат векторов
в этом базисе составим систему линейных уравнений из координат векторов  1,
1, 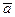 2,
2, 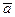 3,
3, 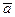 4 и
4 и  и решим ее методом Гаусса:
и решим ее методом Гаусса:
 *
*
Составим матрицу системы и преобразуем ее к треугольному виду, т.е. будем последовательно получать нули ниже главной диагонали матрицы, на которых находятся элементы 2, 2, 8, 3.
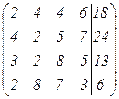
Разделим каждый элемент I строки на 2, затем полученную I строку умножим последовательно на -4; -3; -2 и сложим соответственно со II; III и IV строками, получим:
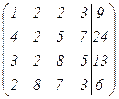 ~
~ 
Разделим III строку на (-2) и поменяем ее местами со II строкой.

Новую II строку умножим последовательно на 3; -2 и сложим соответственно с III и IV строками, получим:
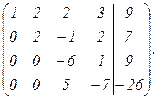
III строку умножим на 5, IV на 6 и сложим их, получим:
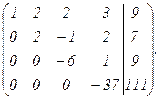
Таким образом получим матрицу ступенчатого вида, например х1, х2, х3, х4,

откуда х4 = 3, х3 = -1, х2 = 0, х1 = 2.
Решение системы * (2; 0; -1; 3) образует совокупность координат вектора  в базисе
в базисе  1,
1, 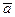 2,
2, 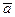 3,
3, 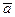 4, т.е. в этом базисе
4, т.е. в этом базисе  (2; 0; -1; 3) или
(2; 0; -1; 3) или  = 2
= 2 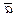 1 -
1 -  3 + 3
3 + 3  4.
4.
Пример 2. Даны координаты вершин пирамиды А1 (2; 1; 0), А2 (3; -1; 2), А3 (13; 3; 10), А4 (0; 1; 4).
Найти: 1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребрами А1А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
Решение.
1) Расстояние d между точками А (х1, y1, z1) и В (х2, y2, z2), определяется по формуле
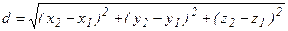 (1)
(1)
Подставим в (1) координаты точек А1 и А2, находим длину ребра А1А2:
А1А2= 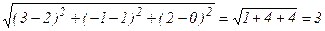
2) Угол между ребрами А1А2 и А1А4 равен углу φ между направляющими векторами этих ребер 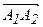 и
и  . Косинус угла между двумя векторами = скалярному произведению этих векторов, деленному на произведение их модулей:
. Косинус угла между двумя векторами = скалярному произведению этих векторов, деленному на произведение их модулей:
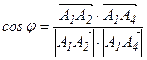 (2)
(2)
Координаты вектора  с началом в точке А1 (x1, y1, z1) и концом в точке А2 (x2, y2, z2)
с началом в точке А1 (x1, y1, z1) и концом в точке А2 (x2, y2, z2)
 (3)
(3)
Применяя (3), получим  (1; -2; 2),
(1; -2; 2), 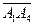 (-2; 0; 4). Применяя (1), получим модули векторов
(-2; 0; 4). Применяя (1), получим модули векторов

Скалярное произведение двух векторов с заданными координатами равны сумме произведений соответствующих координат, т.е если 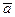 (а1, а2, а3),
(а1, а2, а3),  (
(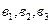 ), то их скалярное произведение
), то их скалярное произведение
 (4)
(4)
Применяя (4), найдем 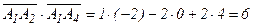 . Следовательно,
. Следовательно,

3) Угол между ребром А1А4 и гранью А1 А2 А3 равен углу φ между направляющим вектором 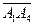 данного ребра и нормальным вектором
данного ребра и нормальным вектором 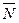 плоскости А1 А2 А3.
плоскости А1 А2 А3.
Уравнение плоскости, проходящей через 3 данные точки А1 (х1, y1, z1) и А2 (х2, y2, z2), А3 (х3, y3, z3) имеет вид
 (5)
(5)
Подставим в (5) координаты точек А1 А2 А3, получим:

Разложим определитель по элементам I строки:
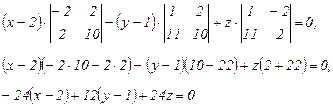
Сократив на (-12), получим уравнение плоскости А1 А2 А3:
2x – 4 – y + 1 - 2z = 0
2x – y - 2z – 3 = 0
Если уравнение плоскости α задано в каноническом виде Ax + By + Cz + Д = 0, то ее нормальный вектор 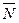 α (А; В; С), т.е. нормальный вектор плоскости А1 А2 А3 имеет координаты
α (А; В; С), т.е. нормальный вектор плоскости А1 А2 А3 имеет координаты 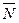 (2; -1; -2). Синус угла α между вектором
(2; -1; -2). Синус угла α между вектором 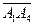 и плоскостью А1 А2 А3
и плоскостью А1 А2 А3
 (6)
(6)
Найдем скалярное произведение 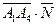 по формуле (4):
по формуле (4):
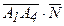 = -2 2 + 0 (-1) + 4 (-2) = - 4 – 8 = -12.
= -2 2 + 0 (-1) + 4 (-2) = - 4 – 8 = -12.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 566; Нарушение авторских прав?; Мы поможем в написании вашей работы!