Контрольная работа №4

260.

259.

258.

257.

256.

255.

254.

253.

252.

251.

180..

Контрольная работа №3

161 - 170. Найти производные 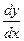данных функций.

161.		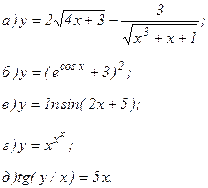162.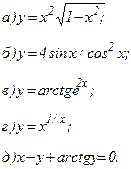
163.		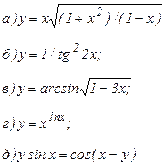164.
165.		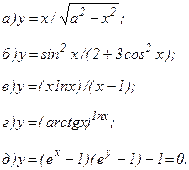166.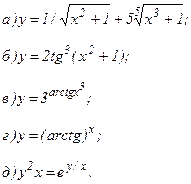
167.		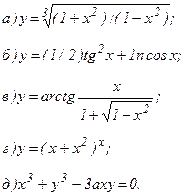168.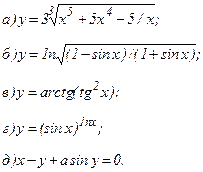
169.		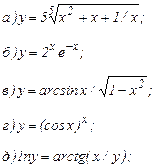170.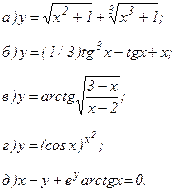

171 - 180. Найт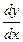и и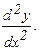

171.

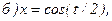
172.

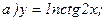
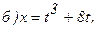
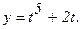
173.

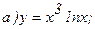
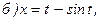
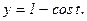
174.

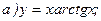
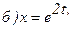
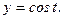
175.

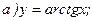
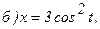
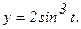
176.

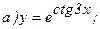
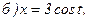
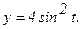
177.

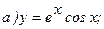
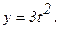
178. ,

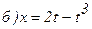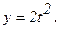
179.

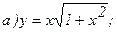
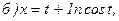
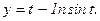
181 - 190. Найти наибольшее и наименьшее значения функции у = f(x) на отрезке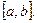

181.

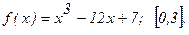
182.

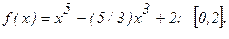
183.

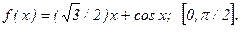
184.

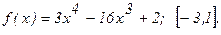
185.

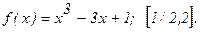
186.

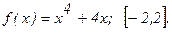
187.

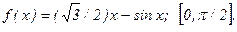
188.

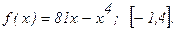
189.

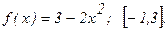
190.

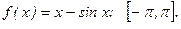
191 - 210. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

191. у = 4х/(4+х²) 192. y = (x²-1)/(x² +1)

193. y = (x²+1)/(x²-1) 194. y = x²/(x-1)

195. y = x³/(x²+1) 196. y = (4x³+5)/x

197. y = (x²-5)/(x-3) 198. y = x⁴/(x³-1)

199. y = 4x³/(x³-1) 200. y = (2-4x²)/(1-4x²)

201. y = (1nx)/ 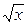202. y = x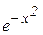

203. y = 204. y = x²-21nx

205. y = 1n (x²-4) 206. y = e^1/(2-x)

207. y = 1n (x²+1) 208. y = (2+x²)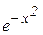

209. y = 1n (9-x²) 210. y = (x-1)e^3x+1.

211. Дана функция z = y/(x²- y²)⁵. Показать, что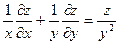

212. Дана функция z = y²/(3x)+arcsin(xy). Показать, что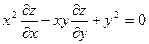

213. Дана функция z = 1n(x²+y²+2x+1). Показать, что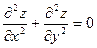

214. Дана функция z = e^xy. Показать, что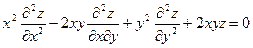

215. Дана функция z = 1n(x+e^-y). Показать, что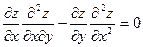

216. Дана функция z = x/y. Показать, что

217. Дана функция z = x^y. Показать, что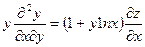

218. Дана функция z = xe^y/x. Показать, что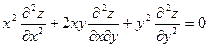

219. Дана функция z = sin(x+ay). Показать, что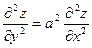

220. Дана функция z = cosy+(y - x)siny. Показать, что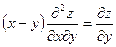

221 - 230. Дана функция z = f(x,y) и две точки А (х₀, у₀) и В (х₁, у₁). Требуется: вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение 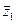функции в точке В, исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С (х₀, у₀, z₀).

221. z = x²+xy+y²; А (1;2), В (1,02;96)

222. z = 3x²-xy+x+y; А (1;3), В (1,06;2,92)

223. z = x²+3xy-6y; А (4;1), В (3,96;1,03)

224. z = x²-y²+6x+3y; А (2;3), В (2,02;2,97)

225. z = x²+2xy+3y²; А (2;1), В (1,96;1,04)

226. z = x²+y²+2x+y-1; А (2;4), В (1,98;3,91)

227. z = 3x²+2y²-xy; А (-1;3), В (-0,98;2,97)

228. z = x²-y²+5x+4y; А (3;3), В (3,02;2,98)

229. z = 2xy+3y²-5x; А (3;4), В (3,04;3,95)

230. z = xy+2y²-2x; А (1;2), В (0,97;2,03).

231 - 240. Найти наименьшее и наибольшее значения функции z = f(x,y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.

231. z = x²+y²-9xy+27; .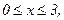

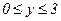232. z = x²+2y²+1; .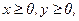

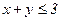233. z = 3-2x²-xy-y²; .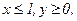

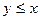234. z = x²+3y²+x-y;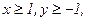

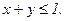
235. z = x²+2xy+2y²; .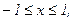

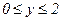236. z = 5x²-3xy+y²+4;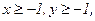

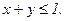
237. z = 10+2xy-x²;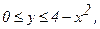

238. z = x²+2xy-y²+4x; .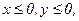

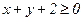239. z = x²+xy-2;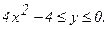

240. z = x²+xy; .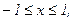

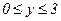241 - 250. Даны функции z = z(x,y), точка А (х₀,у₀) и вектор а. Найти; 1) grad z в точке А; 2)производную в точке А по направлению вектора а.

241. z = x²+xy+y²; А (1;1), а = 2 i - j.

242. z = 2x²+3xy+y²; А (2;1), a = 3i-4 j.

243. z = 1n(5x²+3y²); А (1;1), a = 3i+2 j.

244. z = 1n(5x²+4y²); А (1;1), a = 2 i - j.

245. z = 5x²+6xy; А (2;1), a = i +2 j.

246. z = arctg(xy²); А (2;3), a = 4 i -3 j.

247. z = arcsin (x²/y); А (1;2), a = 5 i -12 j.

248. z = 1n(3x²+4y²); А (1;3), a = 2 i - j.

249. z = 3x⁴+2x²y³; А (-1;2), a = 4 i -3 j.

250. z = 3x²y²+5y²x; А (1;1), a = 2 i + j.

251 - 260. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b.

х
у	4,3	5,3	3,8	1,8	2,3

х
у	4,5	5,5	4,0	2,0	2,5

х
у	4,7	5,7	4,2	2,2	2,7

х
у	4,9	5,9	4,4	2,4	2,9

х
у	5,1	6,1	4,6	2,6	3,1

х
у	3,9	4,9	3,4	1,4	1,9

х
у	5,2	6,2	4,7	2,7	3,2

х
у	5,5	6,5	5,0	3,0	3,5

х
у	5,7	6,7	5,2	3,2	3,7

х
у	5,9	6,9	5,4	3,4	3,9

261 - 270. Найти неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.

261.

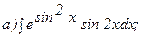
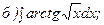
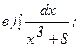
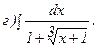
262.

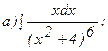
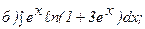
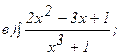
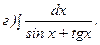
263.

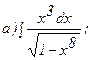
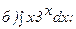
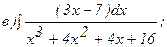
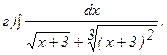
264. ;

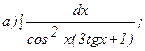
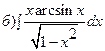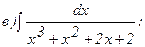
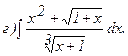
265. ;

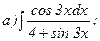
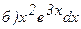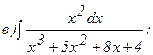
266.

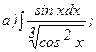
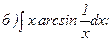
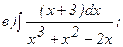
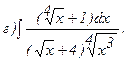
267.

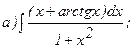
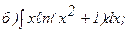
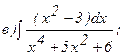
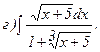
268.

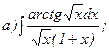
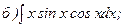
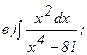
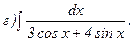
269.

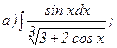
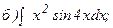
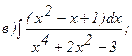
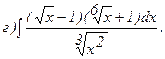
270.

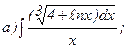
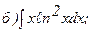
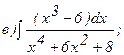
271 - 280. Вычислить приближенное значение определенного интеграла 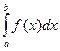с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

271.

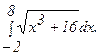
273.

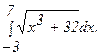
272.

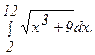
274.

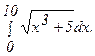
275.

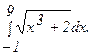
277.

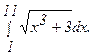
279.

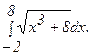
276.

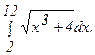
278.

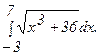
280.

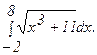
281 - 290. Вычислить несобственный интеграл или доказать его расходимость.

281.

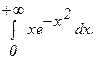
283.

285.

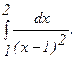
287.

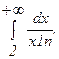
289.

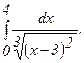
282.

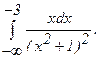
284.

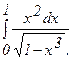
286.

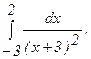
288.

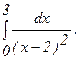
290.

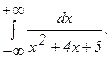
291. Вычислить площадь фигуры, ограниченной параболой у = 3х² + 1 и прямой у = 3х + 7.

292. Вычислить площадь фигуры, ограниченной одной аркой циклоды х = а(t - sin t), y = a(1 - cos t), 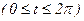и осью Ох.

293. Вычислить площадь фигуры, ограниченной кардиоидой r = 3(1 + cos φ).

294. Вычислить площадь фигуры, ограниченной четырехлепестковой розой r = 4sin 2φ.

295. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами у = х² и у = .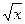

296. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом у = 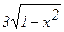, параболой х = 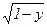и осью Оу.

297. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2/(1 + х²)⁴ и у = х².

298. Вычислить длину дуги полукубической параболы у = 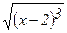от точки А (2;0) до точки В (6;8).

299. Вычислить длину кардиоиды r = 3(1 - cosφ).

300. Вычислить длину одной арки циклоиды х = 3(t - sint), y = 3(1 - cost), .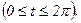

301 - 320. Найти общее решение дифференциального уравнения.

301.

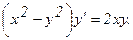
302.

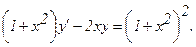
303.

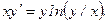
304.

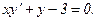
305.

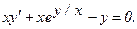
306.

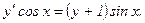
307.

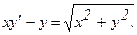
308.

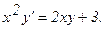
309.

310.

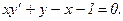
311.

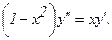
312.

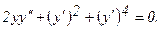
313.

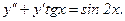
314.

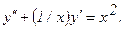
315.

316.

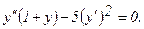
317.

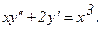
318.

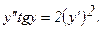
319.

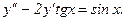
320.

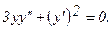
В задачах 321 - 330 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.

321. у΄΄- е^уу΄= 0, у(0) = 0, у΄(0) = 1.

322. у΄у΄΄= 2у, у(0) = 0, у΄(0) = 0.

323. уу΄΄= (у΄)², у(0) = 1, у΄(0) = 3.

324. у³у΄΄= 3, у(1) = 1, у΄(1) = 1.

325. у΄΄-12у²= 0, у(0) =1/2, у΄(0) = 1.

326. 2у΄΄=е^4у, у(0) = 0, у΄(0) = ½.

327. (у – 2)у΄΄ = 2(у΄)², у(0) = 3, у΄(0) = 1.

328. 2уу΄΄= 3 + (у΄)², у(1) = 1, у΄(1) = 1.

329. у΄΄= 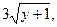у(2) = 0, у΄(2) = 2.

330. (у + 1)²у΄΄= (у΄)³, у΄(0) = 1.

331 - 340. Найти частное решение дифференциального уравнения 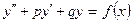, удовлетворяющее начальным условиям у(0)=у₀,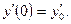

331.

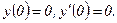
332.

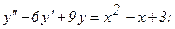
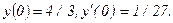
333.

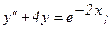
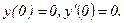
334.

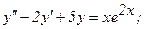
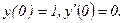
335.

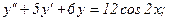
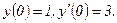
336.

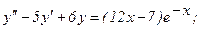
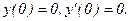
337.

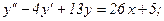
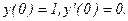
338.

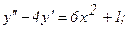
339.

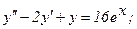
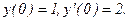
340.

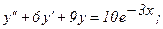
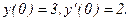
В задачах 441 - 450 даны линейные неоднородные дифференциальные уравнения второго полрядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.

441. y΄΄-2y΄-8y=16x²+2, y(0)=0, y΄(0)=5.

442. y΄΄+4y=3cos x, y(0)=1, y΄(0)=2.

443. y΄΄-y΄-2y=3e^2x, y(0)=2, y΄(0)=5.

444. y΄΄-2y΄=2x+1, y(0)=1, y΄(0)=1.

445. y΄΄-2y΄+y=9e^-2x+2x-4, y(0)=1, y΄(0)=1.

446. y΄΄-4y=4sin 2x, y(0)=2, y΄(0)=7.

447. y΄΄+y΄=3cos x – sin x, y(0)=0, y΄(0)=1.

448. y΄΄-y΄-6y=6x²-4x-3, y(0)=3, y΄(0)=5.

449. y΄΄-3y΄=3e^3x, y(0)=2, y΄(0)=4.

450. y΄΄-4y΄+5y=5x – 4, y(0)=0, y΄(0)=3.

351 - 360. Дана система линейных дифференциальных уравнений с постоянными коэффициентами

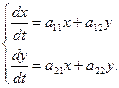
Требуется найти общее решение системы.

351.

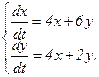
353.

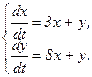
355.

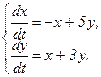
357.

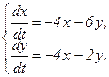
359.

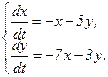
352.

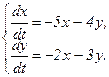
354.

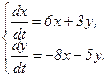
356.

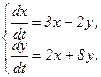
358.

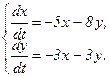
360.

Дата добавления: 2014-11-06