Применяя формулу (1), получим

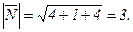
Следовательно,

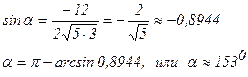
4) Площадь грани А₁ А₂ А₃ равна половине площади параллелограмма, построенного на векторах 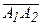и 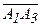. Обозначим через вектор 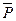векторное произведение векторов 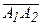и 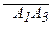, тогда площадь параллелограмма 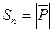, а площадь грани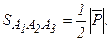

Координаты вектора 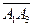найдем по формуле (3):

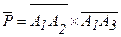
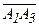(11; 2; 10)

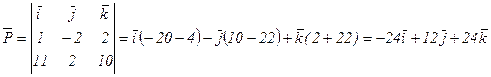
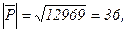
кв. ед.

5) Объем пирамиды V в шесть раз меньше объема параллелепипеда V₁, построенного на трех некомпланарных векторах, и равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение :

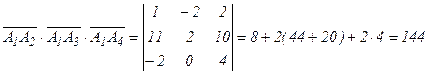
Следовательно, V₁ параллелепипеда равен 144 куб. ед., а объем заданной пирамиды V = 144/6 =24 куб. ед.

6) Уравнение прямой, проходящей через две заданные точки А₁ (х₁, y₁, z₁) и А₂ (х₂, y₂, z₂) имеет вид

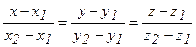(7)

Подставив в (7) координаты точек А₁ и А₂, получим

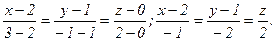
7) Уравнение плоскости А₁А₂А₃ – это уравнение грани А₁А₂А₃, которое найдено в п.3:

А₁А₂А₃ : 2х – у – 2z – 3 = 0

8) Уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃ – это перпендикуляр А₄Д. Каноническое уравнение прямой в пространстве имеет вид

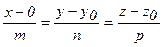(8)

где х₀, у₀, z₀ – координаты точки, через которую проходит прямая (8), а m, n, p – направляющие коэффициенты этой прямой. По условию прямая проходит через точку А₄( 0; 1; 4) и перпендикулярные грани А_!А₂А₃ для которой 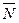(2; -1; -2), т.е. подставив эти данные в формулу (8), получаем

- уравнение высоты А₄Д

Пример 3. Линия задана уравнением 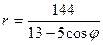в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.

Решение.

1) Построим линию по точкам от φ = 0 до φ = 2π, придавая φ значения через промежуток .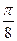

Составим таблицу:

φ	r(φ)
0^0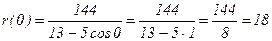
22,5^0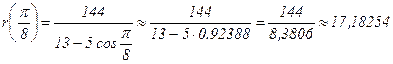
45^0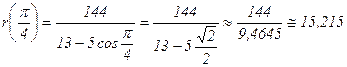
67,5^0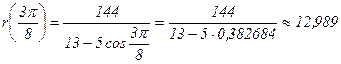
90^0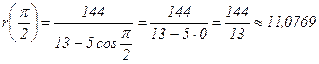
112,5^0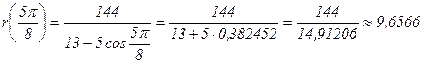
135^0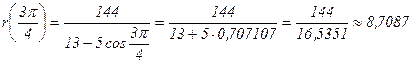
157,5^0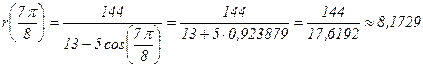
180^0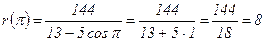
202,5^0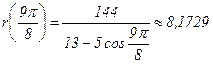
225^0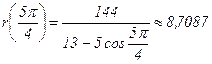
247,5^0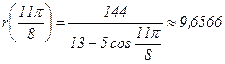
270^0
292,5^0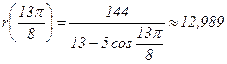
315^0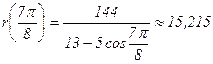
337,5^0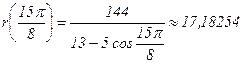
360^0

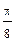
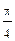
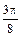
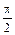
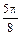
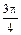
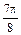
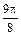
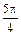
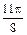
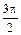
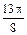
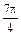
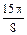
φ	0								π								2π
r	18	17,2	15,2	12,99	11,08	9,66	8,7	8,2	8	8,2	8,7	9,66	11,08	13	15,2	17,2	18

Построим полученные точки в полярной системе координат (рис. 1).

Рис. 1.

2) Найдем уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абцисс ОХ – с полярной осью р.

Для этого воспользуемся формулами перехода к прямоугольной декартовой системе координат х = rcosφ, y = rsinφ, откуда r²=x²+y², 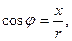тогда подставим эти формулы в данное уравнение 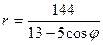, получаем:

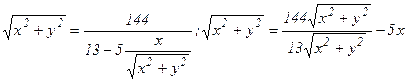
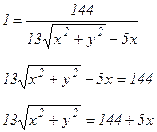
Возведем в квадрат обе части последнего равенства:

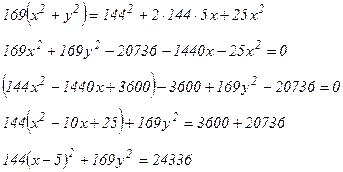
Разделим обе части последнего уравнения на 24336:

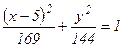
Полученное уравнение – уравнение эллипса с центром в точке А (5; 0), полуоси которого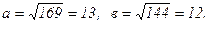

Проверим r(-φ), зная, что cosφ=cos(-φ)

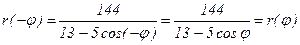
Так как r(-φ)=r(φ), то данная линия будетсимметрична относительно полярной оси р и достаточно найти r(φ) для угловот φ=0 до φ=π.

Пример 4. Данную систему уравнений:

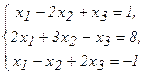
решить по формулам Крамера (через определитель) и средствами матричного исчисления (с помощью обратной матрицы).

Обозначим через А матрицу коэффициентов при неизвестных;

Х – м-цу - столбец неизвестных х₁, х₂, х₃;

В – м-цу – столбец свободных членов:

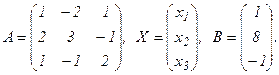
С учетом этих обозначений данная система уравнений примет следующую матричную форму:

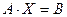(1)

Если матрица А – невырожденная (ее определитель 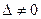), то она имеет обратную матрицу А^-1. умножив обе части уравнения (1) на А^-1, получим:

,

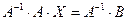но 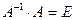- единичная матрица, а ЕХ = Х, поэтому

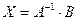(2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо выписать обратную матрицу А^-1.

Пусть имеем невырожденную матрицу 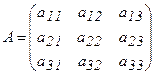и ее определитель равен Δ, тогда 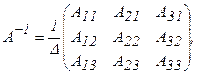где A_ij (i = 1,2,3; j = 1,2,3) – алгебраическое дополнение элемента a_ij в определителе матрицы А и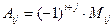

где M_ij – минор (определитель) второго порядка, полученный вычеркиванием i –й строки и j – го столбца в определителе матрицы А.

Вычислим определитель Δ и алгебраические дополнения A_ij элементов матрицы А.

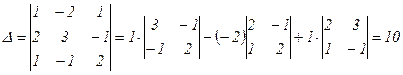
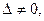следовательно матрица А невырожденная и имеет обратную матрицу А ^-1.

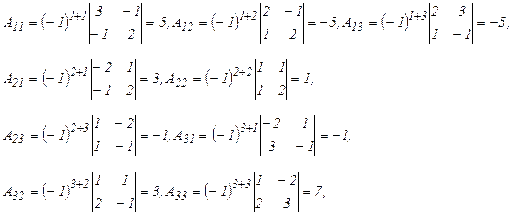
тогда

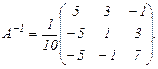
По формуле (2) находим решение данной системы уравнений в матричной форме:

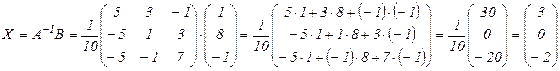
отсюда х₁=3, х₂=0, х₃=-2.

Дата добавления: 2014-11-06