Определение скоростей звеньев механизма с помощью плана скоростей

Кинематическое исследование механизма графоаналитическим методом

Обычно принимается, что кривошип вращается с постоянной угловой скоростью. Линейная скорость точки А кривошипа, как известно, определяется по формуле:

,

где ω₁ - угловая скорость вращения кривошипа, которая определяется по формуле:

^,

class=WordSection2>

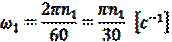где n₁ - число оборотов кривошипа в минуту (мин^-1).

Вектор скорости точки, движущейся по какой-либо траектории, всегда направлен по касательной к траектории в этой точке. В нашем случае вектор скорости точки А направлен по касательной к окружности, т.е. перпендикулярен к радиусу ОА. Из произвольной точки P_V на плоскости проводим отрезок 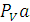произвольной длины (рекомендуется не менее 100 мм) (рис.3), который будет в масштабе 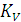(масштабный коэффициент скорости) изображать скорость точки. Величина 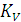будет равна:

^,

class=WordSection3>

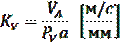т.е. масштабный коэффициент показывает: сколько единиц скорости содержится в одном миллиметре отрезка .

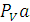Далее определяем скорость точки В, принадлежащей одновременно звеньям 2 и 3. Звено 2 совершает сложное плоскопараллельное движение. В сложном движении скорость точки В определим в соответствии с векторным уравнением:

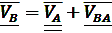,(1)

где 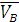- вектор скорости точки В

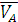- вектор скорости точки А

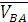- вектор скорости точки В относительно А.

В векторном уравнении (1) скорость точки А известна по величине и по направлению, скорости V_B и V_ВA известны только по направлению. Скорость точки В направлена по линии ОВ (движение ползуна-поршня 3 по направляющим), вектор скорости точки В относительно точки А будет направлен перпендикулярно шатуну АВ как радиусу окружности, описываемой точкой В в ее относительном движении вокруг точки А. В соответствии с этим из точки P_V проводим луч параллельный линии ОВ, а из точки отрезка 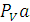луч, перпендикулярный АВ. Пересечение этих лучей в точке 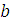является решением векторного уравнения (1) и определяет отрезок 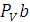, который в принятом масштабе изображает скорость точки В, а отрезок 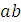изображает скорость точки В относительно точки А.

Направление векторов этих скоростей должно соответствовать уравнению (1), а их величина определяется из соотношений:

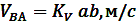
Аналогичным образом определяются скорость точки С и точки С относительно точки А. Положение точек S₂ и S₄ (центров масс), звеньев на плане скоростей определяется в соответствии с условием подобия: их расположение не плане скоростей подобно расположению на схеме механизма. Так, например, если точка S₂ находится на одной трети отрезка АВ, а точка S₂ на плане скоростей будет также находиться на одной трети отрезка . Соединив точки S₂ и S₄ с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из cоотношения:

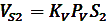, м/c

, м/c

Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении.

Как уже говорилось, отрезок плана скоростей аb (вектор) обозначает скорость точки В относительно точки А. Разделив величину скорости 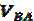на действительную длину звена АВ получим угловую скорость звена 2:

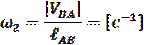
Для определения направления угловой скорости ω₂ необходимо вектор скорости 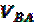приложить к точке В (см. рис 1.), посмотреть в какую сторону звено АВ будет вращаться относительно точки А и в соответствующую сторону направить ω₂. В рассматриваемом случае звено 2 вращается против часовой стрелки.

Угловая скорость звена 4 и ее направление определяются аналогичным образом:

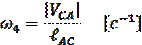
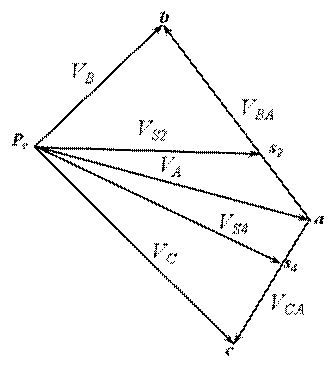
Рис.3 План скоростей

Дата добавления: 2014-11-06