Кинематическое исследование механизмов аналитическими методами

(выполняется по указанию преподавателя)

Кинематическое исследование механизмов методом построения планов скоростей и ускорений позволяет определить с достаточной точностью величину и характер изменения кинематических параметров механизма. Однако построение планов скоростей и ускорений для нескольких положений механизма за весь цикл значительно увеличивает объем проводимой работы, особенно для сложных механизмов. Кроме того, при этом методе значительно усложняется процесс оптимизации кинематических параметров, из-за необходимости многократных построений планов скоростей и ускорений. При использовании вычислительной техники для кинематического исследование механизмов необходимо иметь аналитические зависимости искомых параметров, позволяющие определять их за весь цикл в соответствии с изменениям обобщенных координат.

Одним из методов аналитического исследования кинематики механизмов является метод замкнутых векторных контуров, предложенный В.А. Зиновьевым [ ].

При кинематическом исследовании механизмов этим методом каждое звено механизма представляется в виде вектора определенного направления. Рассмотрим этот метод на примере кривошипно-ползунного механизма (рис.5), в котором кривошип ОА является вектором 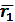, а шатун АВ вектором .

Рис.5 Расчетная схема кривошипно-ползунного механизма

Положение точки B в системе координат xoy обозначено вектором Условие замкнутости векторов при принятом направлении векторов и :

(3)

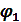Углы и соответственно определяют положение векторов и в выбранной системе координат. Спроектируем эти векторы на оси координат:

(4)

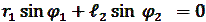(5)

Одной из основных задач в данном случае является нахождение функции изменения кинематических параметров механизма при изменении обобщенной координаты 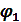. Как следует из уравнения (5):

(6)

Обозначим 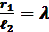- параметр механизма, который в кривошипно-ползунных механизмов транспортных машин изменяется в пределах и определяет их габариты. С учетом формула (6) примет вид:

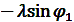(7)

Продифференцируем уравнение (5) по времени при условии .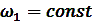

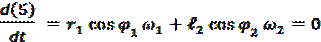(8)

Из уравнения (8) определим угловую скорость шатуна:

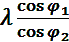(9)

Для определения углового ускорения шатуна продифференцируем уравнение (8):

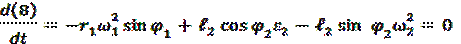
Откуда следует:

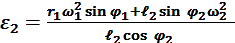(10)

Направление угловых скоростей и ускорений определяется по соответствии их знака принятому положительному направлению отсчета углов и .

В соответствии с (7) формулу (4) представим в виде:

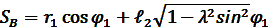
Чтобы избавиться от радикала разложим его в бесконечный ряд Маклорена:

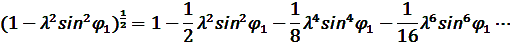
Этот ряд быстро сходится и для практических расчетов при 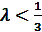достаточно использовать два первых члена. Величина третьего члена при и составляет или 0,05% от единицы.

Таким образом, положение точки B можно приближенно, но с достаточной степенью точности определить по формуле:

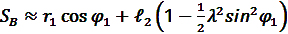(11)

Продифференцировав дважды уравнение (11) получим также приближенные формулы для определения скорости точки B:

(12)

и соответственно ускорения:

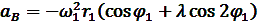(13)

Точное значения ускорения 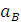представляется в виде бесконечного тригонометрического ряда:

,

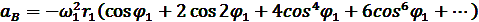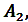
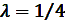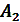коэффициенты, которого определяются в зависимости от величины . В частности, при коэффициент = 0,254, т.е. незначительно отличается от . Для других значений параметра коэффициенты также незначительно отличаются от его величины, что подтверждает возможность использования формул (12) и (13) при различных .

Определим экстремальные значения ускорения точки B. Для этого продифференцируем уравнение (13) по независимому переменному 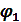и приравняем его к нулю.

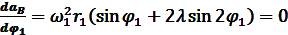(14)

Уравнение (14) дает возможность определить угол 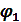, при котором имеет экстремальные значения.Учитывая, что 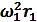не равно нулю, и заменив 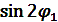его значениями после преобразования получим:

(15)

откуда

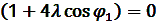(16)

Из уравнения (15) получим значения угла 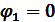и . При этих значениях угла 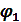имеют место два вида уравнений, определяющих экстремальные значения ускорения :

при :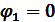

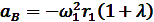
при :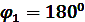

Уравнение (16) добавляет еще два дополнительных экстремальных значения в соответствии с формулой:

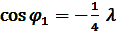
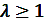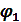Так как , то это уравнение справедливо, если . При этом значении получается два угла (во второй третьей четвертях), при которых ускорение имеет экстремальные значения. Характер изменения ускорения в зависимости от угла 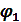для разных значений параметра показан на (рис.6).

При кинематическом исследовании сложного механизма (рис.1), состоящего в общем из двух кривошипно-ползунных механизмов с одним кривошипом, необходимо составить расчетную схему, которая будет зависеть от расположения выбранной системы координат.

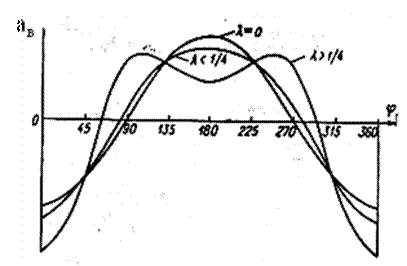
Рис.6 Кривые ускорения точки В центрального кривошипно-ползунного механизма

Дата добавления: 2014-11-06