
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры с решениями. Пример 3.1. Тензор напряжений в точке Р в декартовых осях имеет компоненты
|
|
|
|
Пример 3.1. Тензор напряжений в точке Р в декартовых осях 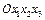 имеет компоненты
имеет компоненты 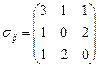 . Определить главные напряжения и главные оси тензора напряжений, с которыми будет связана система осей координат
. Определить главные напряжения и главные оси тензора напряжений, с которыми будет связана система осей координат 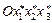 . Показать, что тензор преобразований состоящий из направляющих косинусов приводит первоначальный тензор напряжений к диагональному виду, т.е. оси
. Показать, что тензор преобразований состоящий из направляющих косинусов приводит первоначальный тензор напряжений к диагональному виду, т.е. оси 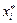 являются главными.
являются главными.
Решение. Главные напряжения определяются по формуле 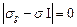 (I - единичная матрица)
(I - единичная матрица)
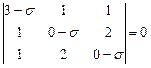 .
.
Вычислим определитель и получим уравнение для главных напряжений 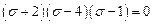 . Откуда
. Откуда 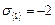 ,
, 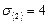 ,
,  , или
, или 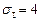 ,
, 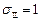 ,
, 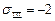 (
(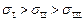 ).
).
Запишем систему уравнений 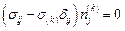 для каждого из главных напряжений. Пусть ось
для каждого из главных напряжений. Пусть ось 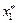 совпадает с осью напряжения s I, и пусть
совпадает с осью напряжения s I, и пусть 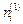 - направляющие косинусы этой оси. Тогда имеем систему
- направляющие косинусы этой оси. Тогда имеем систему
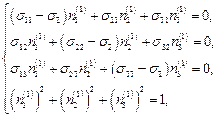 Þ
Þ 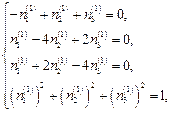
Получим 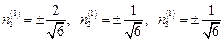 .
.
Пусть ось 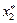 совпадает с осью напряжения s II. Получим
совпадает с осью напряжения s II. Получим
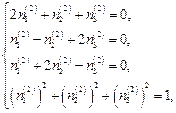 Þ
Þ 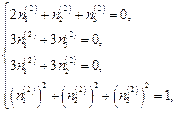
откуда  .
.
Проверим условие ортогональности 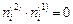
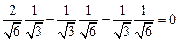 .
.
Т.к. условие ортогональности выполняется возможны следующие варианты
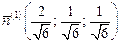 и
и 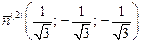 ,
,
или 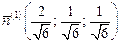 и
и 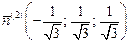 ,
,
или 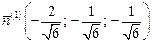 и
и 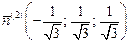 ,
,
или 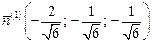 и
и 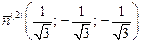 .
.
Аналогично находим третье направление. Пусть ось 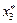 совпадает с осью напряжения s III, и пусть
совпадает с осью напряжения s III, и пусть 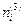 - направляющие косинусы этой оси. В этом случае система имеет вид:
- направляющие косинусы этой оси. В этом случае система имеет вид:
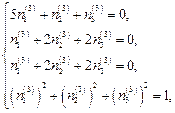
Для нахождения направляющих косинусов третьей оси можно воспользоваться тем, что главные направления попарно ортогональны и найти 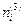 , как
, как 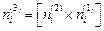 . Тогда
. Тогда
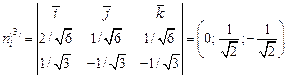
или
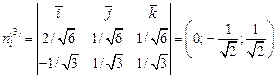 .
.
Покажем, что тензор преобразований, состоящий из направляющих косинусов приводит первоначальный тензор напряжений к диагональному виду. Используя формулу  , где
, где
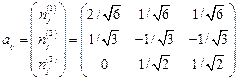
получим:
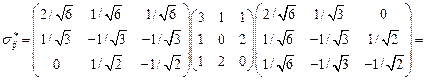
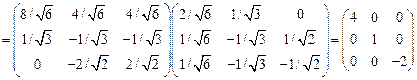 .
.
Что и требовалось показать.
Пример 3.2. В пространстве главных напряжений определить касательное и нормальное напряжения для тензора 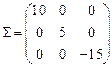 .
.
Решение. Главные значения тензора имеют вид 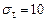 ,
, 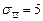 ,
, 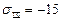 . Т.к. тензор записан в главных осях, то главные направления равны
. Т.к. тензор записан в главных осях, то главные направления равны 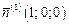 ,
, 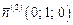 и
и 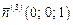 . Применяя формулы (3.9) и (3.10), получим
. Применяя формулы (3.9) и (3.10), получим
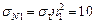 ,
, 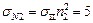 ,
, 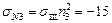 ,
,
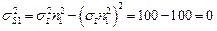 ,
, 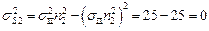 ,
,
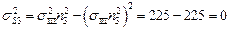 .
.
Полученное решение можно подтвердить используя метод Лагранжа. Т.к. 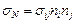 и
и 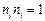 , то функция Лагранжа примет вид
, то функция Лагранжа примет вид 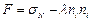 и
и 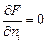 . Тогда
. Тогда
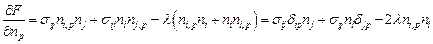 ,
,
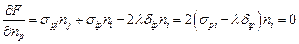 .
.
Полученное уравнение эквивалентно уравнению 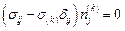 для поиска главных направлений. Отсюда видно, что
для поиска главных направлений. Отсюда видно, что 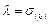 т.е значения нормального напряжения совпадают с главными напряжениями.
т.е значения нормального напряжения совпадают с главными напряжениями.
Ответ: 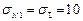 ,
, 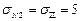 ,
,  ,
, 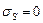 .
.
Пример 3.3. Используя соотношение 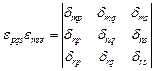 и закон преобразования напряжений
и закон преобразования напряжений 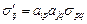 , показать, что произведение
, показать, что произведение 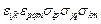 является инвариантом.
является инвариантом.
Решение. Раскрывая определитель 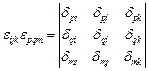 получим
получим 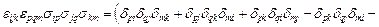
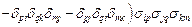 =
= 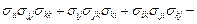
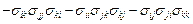 .
.
С учетом симметрии тензора имеем
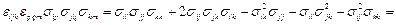
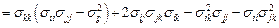
Пример 3.4. Доказать, что 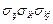 инвариант тензора напряжений.
инвариант тензора напряжений.
Решение. По правилу преобразования компонент тензора 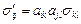 , покажем, что величина
, покажем, что величина 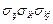 не меняется при смене системы координат
не меняется при смене системы координат

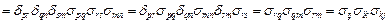
Задания для самостоятельного решения по теме
«Главные напряжения. Круги Мора»
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 3405; Нарушение авторских прав?; Мы поможем в написании вашей работы!