
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры с решениями. Пример 4.1. Разложить тензор напряжений на шаровую часть и девиатор
|
|
|
|
Пример 4.1. Разложить тензор напряжений 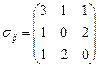 на шаровую часть и девиатор.
на шаровую часть и девиатор.
Решение. Вычислим среднее значение нормального напряжения 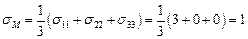 , следовательно, шаровой тензор имеет вид
, следовательно, шаровой тензор имеет вид 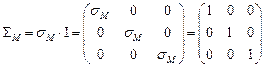 .
.
Тензор девиатора напряжений найдем по формуле 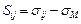
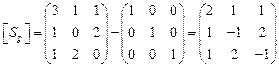 .
.
Пример 4.2. Составить характеристическое уравнение для девиатора напряжений и определить его инварианты, если компоненты тензора напряжений имеют вид 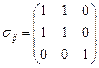 .
.
Решение. Вычислим среднее значение нормального напряжения 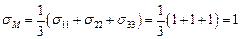 , тензор девиатора напряжений найдем по формуле
, тензор девиатора напряжений найдем по формуле 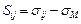
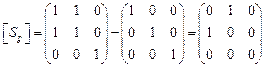 .
.
Для составления характеристического уравнения запишем и раскроем определитель:
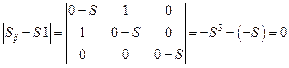 .
.
Получили уравнение 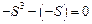 или
или 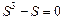 . Проводя аналогию с характеристическим уравнением общего вида
. Проводя аналогию с характеристическим уравнением общего вида 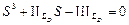 , получаем, что второй инвариант
, получаем, что второй инвариант 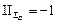 , третий инвариант
, третий инвариант 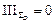 , первый инвариант девиатора всегда равен нулю.
, первый инвариант девиатора всегда равен нулю.
Пример 4.3. Показать, что девиатор напряжений эквивалентен суперпозиции пяти состояний простого сдвига.
Решение. Используем для девиатора напряжений следующее разложение
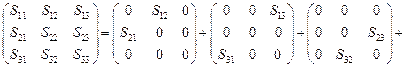
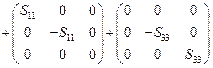
в данном разложении использовалось свойство первого инварианта девиатора напряжений 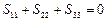 Þ
Þ 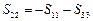 . Покажем, что два последних тензора эквивалентны состоянию простого сдвига. Т.к.
. Покажем, что два последних тензора эквивалентны состоянию простого сдвига. Т.к. 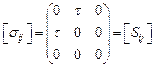 , тогда
, тогда 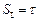 ,
, 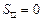 ,
, 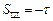 .
.
Пример 4.4. Показать, что разложить тензор напряжений 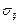 на шаровую часть и девиатор можно только единственным образом.
на шаровую часть и девиатор можно только единственным образом.
Решение. Предположим, что существуют два разложения 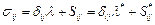 , для которых
, для которых 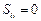 и
и 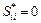 . Тогда
. Тогда 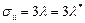 и, следовательно,
и, следовательно, 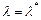 , а из условия
, а из условия 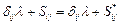 следует, что
следует, что 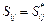 .
.
Задания для самостоятельного решения по теме
«Плоское напряженное состояние. Разложение тензора напряжений на шаровую часть и девиатор»
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 4548; Нарушение авторских прав?; Мы поможем в написании вашей работы!