
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Заміна змінної у визначеному інтегралі
|
|
|
|
Основні правила інтегрування.
Теорема 5: Нехай задано інтеграл 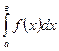 , де
, де 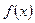 неперервна на відрізку
неперервна на відрізку 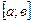 . Зробимо підстановку
. Зробимо підстановку 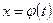 , де
, де 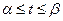 , де
, де 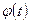 неперервно диференційована функція на відрізку
неперервно диференційована функція на відрізку 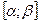 .
.
Якщо:
1) При зміні 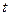 від
від  до
до 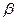 змінна
змінна 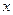 змінюється від
змінюється від  до
до 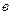 , тобто
, тобто 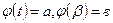 ;
;
2) Складна функція  визначена і неперервна на відрізку
визначена і неперервна на відрізку 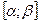 , тоді має місце рівність
, тоді має місце рівність  .
.
Ця формула називається формулою заміни змінної або підстановки у визначеному інтегралі.
Помічаємо, що при обчисленні визначеного інтеграла за допомогою заміни змінної немає потреби повертатися до попередньої змінної, так як це робилось при обчисленні невизначеного інтеграла, тому що визначений інтеграл представляє собою число, яке відповідно попередній формулі дорівнює значенню кожного з розглядуваних інтегралів. Тепер при підстановці зразу потрібно знайти нові границі інтегрування і потім виконати необхідні перетворення підінтегральної функції.
Помічаємо також, що при заміні змінної у визначеному інтегралі необхідно врахувати умови теореми 5, інакше можна одержати неправильний результат (особливу увагу потрібно звертати на виконання умов 1 і 2).
Обчислити визначені інтеграли методом підстановки:
Приклад 1:  .
.
Розв’язування: Виконаємо підстановку  . Тоді
. Тоді 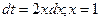 , то
, то 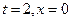 то
то  . Оскільки функція
. Оскільки функція 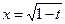 - неперервна на
- неперервна на 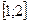 , то і нова функція також неперервна, значить всилу теореми 5 існує первісна на цьому відрізку. Одержимо
, то і нова функція також неперервна, значить всилу теореми 5 існує первісна на цьому відрізку. Одержимо  .
.
Приклад 2: 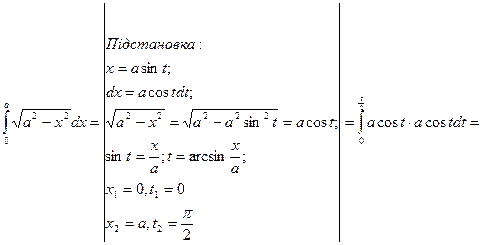
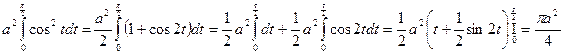 ;
;
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 5797; Нарушение авторских прав?; Мы поможем в написании вашей работы!