Невласні інтеграли

Об’єм тіла обертання та площі поверхні тіла обертання.

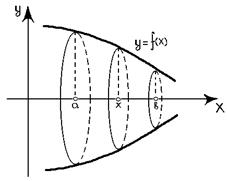Нехай криволінійна трапеція, обмежена кривою , відрізком 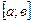осі та прямими та обертається навколо осі (рис 3.). Тоді об’єм тіла обертання можна знайти за формулою , а площу поверхні обертання за формулою .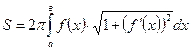

Приклад: Обчислити об’єм кулі радіуса .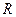

Розв’язування. Кулю можна розглядати як результат обертання полукруга, обмеженого частиною кола 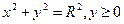, навколо осі 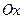. Використовуючи рівність 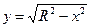, симетричність кола відносно осі та формулу 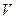, одержимо 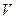кулі:

.

Згідно з теоремою існування визначеного інтеграла цей інтеграл існує, якщо виконані умови:

1) відрізок інтегрування 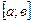скінчений;

2) підінтегральна функція 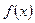неперервна або обмежена і має скінчену кількість точок розриву.

Якщо хоч одна з умов не виконується, то визначений інтеграл називають невласним.

Дата добавления: 2014-11-06