Декартов прямоугольный базис. Декартова прямоугольная система координат

Геометрически построение разложений вектора по базису на плоскости или в пространстве приводит к построению параллелограммов и параллелепипедов. Естественно выбирать такой базис, для которого подобное построение наиболее просто. Поэтому будем выбирать такой базис, в котором векторы попарно перпендикулярны (или, как говорят в векторной алгебре, попарно ортогональны) и имеют длины, равные единице.

Для того чтобы связать векторный метод решения задач с методом координат, удобно рассматривать базис в его связи с системой координат. Задание прямоугольной системы координат на плоскости или в пространстве прежде всего предполагает, что выбрана одна определенная единица длины, посредством которой измеряются длины всех отрезков.

На плоскости прямоугольную систему координат (СК) ОХY образует упорядоченная пара взаимно перпендикулярных осей. Первая ось с единичным вектором 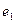называется осью абсцисс ОХ, вторая ось с единичным вектором 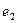- осью ординат ОY. Точка пересечения осей О называется началом системы координат. Векторы 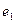и 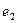образуют базис, а их направления определяют положительные полуоси ОХ и ОY соответственно. Различают правые и левые системы координат. Прямоугольная система координат на плоскости называется правой, если поворот на угол 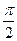положительной полуоси ОХ до совмещения с положительной полуосью ОY происходит против хода часовой стрелки. В противном случае система координат называется левой. Далее мы будем рассматривать только правые системы координат. Если система координат правая, то орт оси абсцисс обозначают 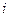, а орт оси ординат- .

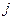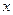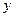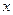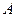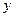Пусть А – произвольная точка плоскости. Вектор называется радиусом –вектором точки А, а его координаты- координатами точки А. Первая координата точки А называется ее абсциссой, а вторая – ординатой. Если абсцисса и ордината точки А есть и соответственно, то принято писать . Нетрудно видеть, что абсцисса точки есть скалярная проекции вектора на ось , а ордината точки 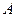есть скалярная проекция вектора на ось .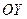

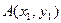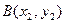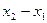Теорема 1. Если заданы координаты точек А и В, т.е. , , то координаты вектора равны и 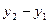соответственно: .

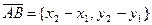В пространстве прямоугольную СК образует упорядоченная тройка взаимно перпендикулярных осей, пересекающихся в общей точке О, называемой началом СК. К осям абсцисс ОХ с единичным вектором 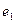и ординат ОY с единичным вектором 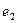, прибавляется ось аппликат OZ с единичным вектором 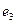. Векторы 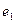, 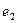и 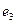образуют базис в пространстве, а их направления определяют положительные полуоси ОX, ОY и OZ соответственно.. Различают правую и левую системы координат. CК называется правой, если из конца вектора 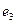поворот на угол 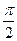положительной полуоси ОХ до совмещения с положительной полуосью ОY видится происходящим против хода часовой стрелки. В противном случае система координат называется левой. Далее мы будем рассматривать только правые системы координат. Если система координат правая, то орт оси абсцисс обозначают 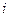, орт оси ординат- 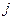, орт оси аппликат- .

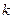Также как в плоском случае радиусом-вектором точки 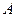называется вектор , а координаты вектора называются координатами точки 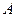. Теперь у каждой точки три координаты-абсцисса, ордината и аппликата, которые равны скалярным проекциям вектора на оси OX, OY и OZ соответственно.

Как и в плоском случае, для того чтобы найти координаты вектора с заданными началом и концом, нужно из координат конца вектора вычесть координаты его начала: если 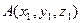, , 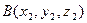то .

Отметим следующие свойства векторов:

1) На плоскости вектор .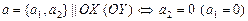

2) В пространстве вектор 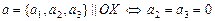(соответственно , ).

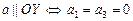3) Вектор 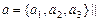плоскости 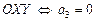(соответственно , ).

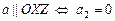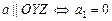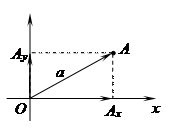Используя прямоугольные координаты, легко получить формулу вычисления длины вектора. Пусть 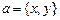. Приложив его к началу координат О, имеем 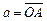. Пусть 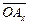, 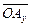– векторные проекции вектора а на оси ОХ и ОY соответственно. Тогда

, .

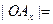
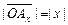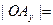
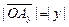Из прямоугольного треугольника находим по теореме Пифагора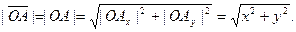

В пространстве, если 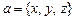, то .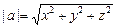

Легко получить и формулу длины отрезка с концам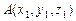и и 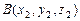. Так как 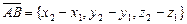, то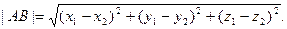

Дата добавления: 2014-11-06