Векторное произведение векторов

Как понятие скалярного произведения возникает из понятия работы, так понятие векторного произведения возникает из понятия момента силы.

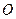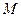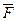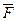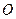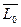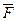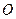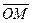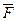Пусть твердое тело имеет одну неподвижную точку . Пусть к точке этого тела приложена сила . Из физики известно, что воздействие этой силы на тело с неподвижной точкой характеризуется особой векторной величиной , которая называется моментом силы относительно точки . Модуль момента равен площади параллелограмма, построенного на векторах и . Направлен момент 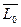по перпендикуляру к плоскости, проходящей через точку 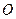и силу 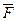, в ту сторону, откуда вращение тела вокруг точки 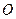, вызываемое силой 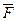, видно происходящим против хода часовой стрелки. Момент силы 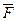относительно точки 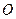и называется векторным произведением вектора 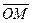, соединяющего точку 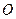с точкой 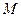приложения силы, и вектора силы .

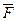Перейдем теперь к общим определениям.

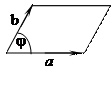
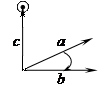Определение 1. Рассмотрим в пространстве упорядоченную тройку некомпланарных векторов а, b, с. Тройка векторов а, b, с называется правой (левой), если наименьший поворот вектора 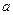до совмещения его с вектором 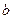виден из конца вектора происходящим против хода (по ходу) часовой стрелки. На рисунке изображена левая тройка векторов а, b, с.

Определение 2. Пусть имеется упорядоченная пара векторов а и b. Если векторы а и b коллинеарны, то их векторное произведение [ a, b ] равно 0. В противном случае векторным произведением [ a, b ] векторов а и b называется вектор n, длина и направление которого задаются условиями:

1) .

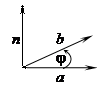
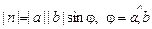2) .

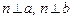3) 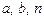– правая тройка.

Из определения векторного произведения следует, что модуль векторного произведения 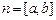ненулевых векторов а и b есть площадь параллелограмма, построенного на векторах а и b. Из определения векторного произведения также следует, что

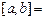0 .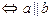

Теорема 1 (Законы векторного произведения).

1) (антикоммутативность);

2) 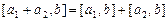(аддитивность).

3) .

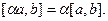Свойства 2) и 3) называются линейностью векторного произведения по первому аргументу. Нетрудно видеть, что векторное произведение векторов линейно также и по второму аргументу, т.е.

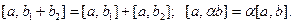
Введём теперь СК OXYZ. Очевидно, для ортов координатных осей справедливы равенства:

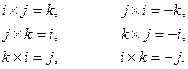
Используя эти равенства и линейность векторного произведения векторов как по первому, так и по второму аргументам, получаем следующую теорему.

Теорема 2. Пусть векторы а и b заданы координатами: 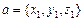, 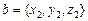. Тогда вектор 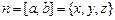, где

, , .

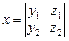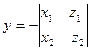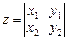Замечание 1. Для вычисления координат 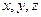можно использовать разложение по первой строке определителя матрицы, составленной из базиса 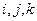и координат векторов а и b:

.

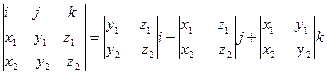Следствие 1. Зная координаты векторного произведения, можно получить формулу для вычисления площади параллелограмма, построенного на векторах а и b:

S _▱= .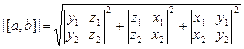

Замечание 2. Векторы 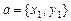и 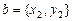можно рассматривать лежащими

на плоскости ОХY. Тогда координаты 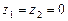, и для площади параллелограмма, построенного на векторах а и b, мы получаем формулу:

S _▱= .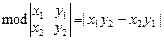

Дата добавления: 2014-11-06