Прямые в пространстве

Подобно тому, как это делалось в плоском случае, для прямых в пространстве вводится понятие направляющего вектора и угла между двумя прямыми.

Введем в пространстве СК OXYZ. Если прямая задана точкой и

направляющим вектором 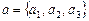, то также, как и в случае прямой на плоскости, получаем каноническое уравнение прямой и параметрические уравнения прямой

Так же, как и в плоском случае, из канонического уравнения прямой можно получить уравнение прямой, проходящей через две различные точки и : .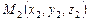

Пусть прямая d определена точкой 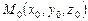и направляющим вектором 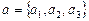. Обозначим через 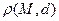расстояние от точки до прямой d, которое, как и в плоском случае,есть длина перпендикуляра 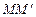, опущенного из точки М на прямую d.

Теорема 1. .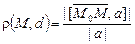

В прямоугольных координатах формула расстояния будет иметь вид

.

Напомним, что две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Если прямые нескрещивающиеся, т.е. лежат в одной плоскости, то они могут быть параллельными, пересекающимися и совпадающими.

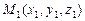Пусть прямая задана точкой и направляющим вектором , а прямая 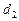– точкой и направляющим вектором

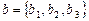. Составим матрицы и 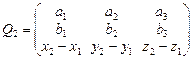. Пусть 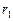– ранг 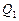, 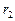– ранг .

Теорема 2.

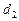1) и скрещивающиеся Û ;

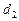2) и пересекаются Û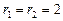

3) 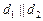Û , ;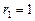

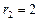4) .

Напомним, что общим перпендикуляром двух скрещивающихся прямых называется отрезок, удовлетворяющий условиям:

1) один конец отрезка лежит на одной прямой, а другой - на другой;

2) прямая, содержащая отрезок, перпендикулярна каждой из двух прямых.

Можно показать, что общий перпендикуляр к скрещивающимся прямым и 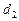существует и его длина равна высоте параллелепипеда, построенного на векторах а, b, 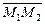, проведённой к основанию, построенному на векторах а и b.

Расстоянием между скрещивающимися прямыми и 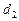называется длина общего перпендикуляра к обеим прямым.

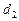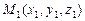Теорема 3. Пусть прямые и скрещивающиеся, прямая задана точкой и направляющим вектором , а прямая 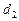– точкой и направляющим вектором 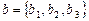. Тогда

.

Дата добавления: 2014-11-06