Кривые второго порядка: окружность, эллипс, гипербола, парабола

Если на плоскости задана система координат OXY, то уравнение F (x, y) = 0является уравнением линии (или кривой) второго порядка, если F (x, y)представляет из себя алгебраический многочлен второго порядка. Общий вид такого многочлена может быть записан в виде:

F (x, y) = ,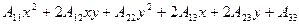

где коэффициенты 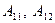и 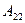одновременно не обращаются в 0.

Окружность.

Определение 1. Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии r от некоторой точки C. Точка C называется центром окружности.

Введем на плоскости CK OXY, ипусть точка C имеетабсциссу 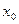и ординату 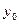. Тогда уравнение 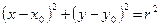будет уравнением окружности. Если мы поместим начало координат в центр C, то получим уравнение .

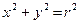Эллипс.

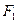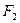Определение 2. Эллипсом называется множество точек плоскости, сумма расстоянии которых до двух заданных точек плоскости и , называемых фокусами, есть постоянная величина 2 а, большая расстояния 2 с между фокусами.

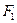Построим систему координат OXY: ось OX будет проходить через фокусы и 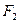, начало координат поместим в середину отрезка .

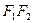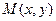Имеем , и для точек на эллипсе выполняется уравнение 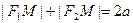. Распишем его в координатах: 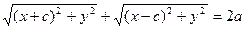. Производя дважды возведение в квадрат и полагая 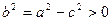, получим уравнение эллипса

,

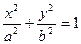которое называется каноническим. Таким образом, эллипс – кривая второго порядка.

Отметим свойства эллипса. Так как в уравнении эллипса х иу участвуют в чётной степени, то эллипс имеет две оси симметрии: одна проходит через фокусы 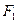и 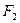, вторая ось симметрии проходит через середину отрезка 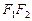перпендикулярно первой оси. Точка пересечения осей симметрии является центром симметрии эллипса. В построенной нами системе координат оси симметрии эллипса совпадают с осями OX и OY, а центр симметрии – с началом координат. Учитывая отмеченную симметрию, для изображения эллипса нужно построить его часть, которая лежит в первом квадранте (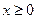, 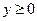), а затем симметрично отобразить её относительно осей и центра симметрии. Для точек эллипса 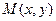имеем , .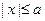

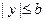Определение 3. Точки пересечения эллипса с осями симметрии называются вершинами эллипса: это , , , .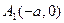

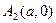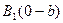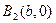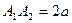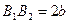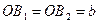Определение 4. Отрезок называют большой осью, – малой осью эллипса. Соответственно - большая полуось, – малая полуось эллипса.

Определение 5. Отношение 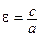называется эксцентриситетом эллипса. Очевидно для эллипса 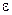<1. Эксцентриситет эллипса – это мера его сплюснутости: чем меньше эксцентриситет эллипса, тем меньше отличаются его полуоси.

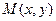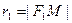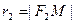Определение 6. Для каждой точки на эллипсе и называются фокальными радиусами точки M.

Для фокальных радиусов справедливы равенства

, .

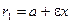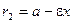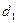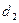Определение 7. Прямые и , перпендикулярные большой оси эллипса и отстоящие от центра симметрии эллипса на расстояние 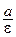, называются директрисами эллипса.

Так как 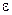<1, то 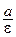> a. Поэтому директрисы эллипса отстоят от его центра симметрии дальше, чем его вершины 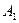и 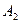. Уравнениями директрис будут: .

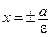Фокус и ближайшая к нему директриса будут называться односторонними.

Теорема 1. Отношение расстояний любой точки эллипса до односторонних фокуса и директрисы есть величина постоянна, равная

Пример 1. Найти эксцентриситет и директрисы эллипса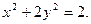

Решение. Написав уравнение эллипса в виде

,

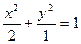заключаем, что 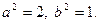Следовательно, 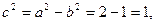откуда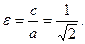

Директрисы проходят на расстоянии 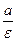от центра эллипса (начала координат), т.е. на расстоянии, равном 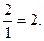Соответственно, уравнения директрис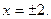

Гипербола.

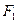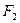Определение 8. Гиперболой называется множество точек плоскости, абсолютное значение разности расстояний которых до заданных точек и , называемых фокусами, есть постоянная величина 2 а, меньшая, чем расстояние 2 с между фокусами.

Систему координат OXY строим также как и для эллипса.

Тогда имеем , , 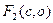и уравнение гиперболы будет - = .

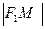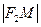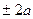Распишем его в координатах . Дважды возводя в квадрат и полагая 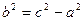, получим уравнение гиперболы

,

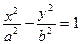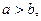
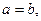
которое называется каноническим. Для гиперболы возможны все три случая: 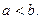Если 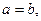то гипербола называется равносторонней.

Отметим свойства гиперболы. Гипербола имеет две оси симметрии. Первая ось симметрии проходит через фокусы и называется действительной осью гиперболы; вторая ось симметрии проходит через середину отрезка 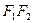, перпендикулярно действительной оси, и называется мнимой осью гиперболы. Точка пересечения осей симметрии гиперболы является центром симметрии этой гиперболы. В построенной нами системе координат оси симметрии гиперболы совпадают с осями OX и OY, а ее центр симметрии – с началом координат.

Определение 9. Точки пересечения гиперболы 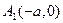и 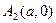с ее действительной осью называются вершинами гиперболы.

С мнимой осью точек пересечения у гиперболы нет.

Определение 10. Расстояние а называется действительной полуосью, b – мнимой полуосью

Для точек 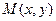на гиперболе, как это следует из ее канонического уравнения, абсциссы точек удовлетворяют условиям 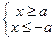, т. е. гипербола состоит из двух различных ветвей: правой () и левой ().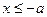

В силу отмеченной симметрии достаточно построить гиперболу в первом квадранте (x 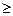0, y 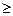0). В этом случае .

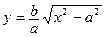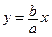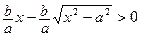Если рассмотреть прямую l c уравнением , то . Поэтому в первом квадранте гипербола находится под прямой l. Кроме того

= = =

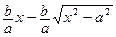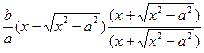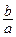
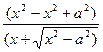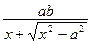
т.е. гипербола по мере увеличения абсцисс её точек приближается (не пересекаясь) к прямой l. Прямая l 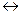у = 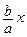называется асимптотой гиперболы.

Производя симметричные отображения, получим рисунок,

из которого очевидно, что прямую 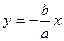также следует назвать асимптотой этой гиперболы.

Критерием того, что гипербола равносторонняя, является взаимная перпендикулярность её асимптот.

Определение 11. Отношение 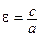называется эксцентриситетом гиперболы..

Очевидно для гиперболы 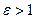. Из определения получаем формулу 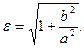Отношение 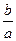равно тангенсу половины угла между асимптотами гиперболы. Поэтому эксцентриситет гиперболы является характеристикой угла между асимптотами гиперболы.

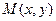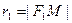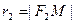Определение 12. Для каждой точки на гиперболе и называются фокальными радиусами точки M.

Для фокальных радиусов точки 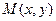на гиперболе справедливы равенства

, .

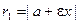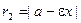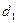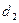Определение 13. Прямые и , перпендикулярные действительной оси гиперболы и отстоящие от центра симметрии гиперболы на расстояние 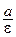, называются директрисами гиперболы.

Так как 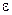<1, то 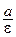> a. Поэтому директрисы гиперболы отстоят от ее центра симметрии дальше, чем ее вершины 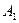и 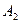. Уравнениями директрис гиперболы будут: .

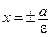Как и в случае эллипса, фокус гиперболы и ближайшая к нему директриса этой гиперболы будут называться односторонними.

Так же как и для эллипса справедлива

Теорема 2. Отношение расстояния точек гиперболы до фокуса к расстоянию до односторонней с фокусом директрисы равно эксцентриситету.

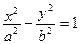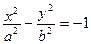Гиперболы с уравнениями и называются сопряженными. У них совпадают оси симметрии и асимптоты.

Парабола.

Определение 14. Параболой называется множество точек плоскости, расстояния которых до заданной точки F, называемой фокусом, и до заданной прямой d, называемой директрисой, равны.

Расстояние 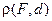от фокуса F до директрисы d обозначается через р и называется параметром параболы.

Строим систему координат. Ось ОХ проводим через фокус, перпендикулярно директрисе.

Если через Q обозначим точку пересечения оси ОХ и директрисы, то начало координат будет находиться в середине отрезка FQ. Допустим, что положительная полуось ОХ направлена в сторону фокуса.

В построенной СК 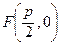, директриса d будет иметь уравнение .

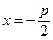Для точек 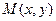параболы имеем, 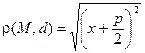, приравнивая эти расстояния, получаем уравнение параболы 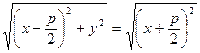, возводя в квадрат, получаем каноническое уравнение параболы

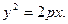
Отметим свойства параболы. Парабола симметрична относительно оси ОХ, т.е. прямой, проходящей через фокус перпендикулярно директрисе. Эта ось симметрии называется осью параболы. Парабола пересекает ось в единственной точке, делящей пополам перпендикуляр от фокуса до директрисы и называемой вершиной параболы. Построим параболу. Из уравнения 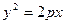следует, что 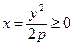. Поэтому построим часть параболы в первом квадранте (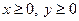), а затем симметрично отобразим ее относительно оси ОХ. Очевидно, что с увеличением y возрастает и х, (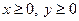), поэтому парабола будет иметь указанный на рисунке вид.

Если положительная полуось ОХ будет направлена в сторону директрисы, то уравнение параболы будет иметь вид .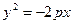

Если фокус параболы будет лежать на оси ОY в точке 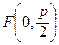(или 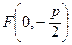), то уравнением параболы будет 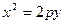(или ).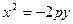

Дата добавления: 2014-11-06