
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие функции
|
|
|
|
Рассмотрим множество 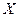 элементов
элементов 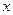 и множество
и множество 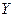 элементов
элементов  .
.
Определение1. Если каждому элементу множества 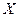 поставлен в соответствие по определенному закону единственный элемент множества
поставлен в соответствие по определенному закону единственный элемент множества 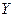 , то говорят, что задано отображение
, то говорят, что задано отображение  множества
множества 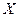 во множество
во множество 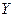 .
.
Слова функция и отображение являются синонимами. Каждая из записей:
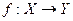 и
и 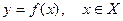 означает, что
означает, что  есть отображение множества
есть отображение множества 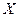 во множество
во множество 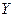 .
.
Элемент  , который отображение
, который отображение  ставит в соответствие элементу
ставит в соответствие элементу 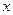 , называется образом элемента
, называется образом элемента 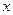 при отображении
при отображении  или значением отображения
или значением отображения  в точке
в точке 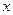 . При этом пишут
. При этом пишут 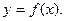
Множество 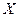 называется областью определения функции
называется областью определения функции  , множество всех значений функции
, множество всех значений функции  – множеством значений этой функции.
– множеством значений этой функции.
Определение 2. Если 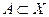 , то множество
, то множество 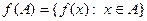 называется образом множества
называется образом множества 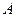 при отображении
при отображении  . Таким образом, область значений
. Таким образом, область значений  есть образ множества
есть образ множества 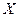 .
.
Определение 3. Графиком функции  называется множество всех пар
называется множество всех пар 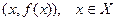 .
.
Определение 4. Говорят, что функция 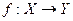 взаимно однозначна, если она разным элементам множества
взаимно однозначна, если она разным элементам множества 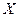 ставит в соответствие разные элементы множества
ставит в соответствие разные элементы множества 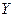 .
.
Определение 5. Пусть 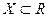 ,
, 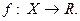 Функция
Функция  называется возрастающей (убывающей), если
называется возрастающей (убывающей), если
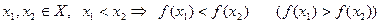 . (1)
. (1)
Если в (1)  неравенства справа нестрогие, то функция
неравенства справа нестрогие, то функция  называется неубывающей (невозрастающей). Функция одного из указанных типов называется монотонной.
называется неубывающей (невозрастающей). Функция одного из указанных типов называется монотонной.
Очевидно возрастающая (убывающая) функция взаимно однозначна.
Определение 6. Пусть функция 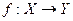 взаимно однозначна и множество ее значений есть
взаимно однозначна и множество ее значений есть 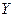 . Функция, которая каждому элементу
. Функция, которая каждому элементу  множества
множества 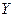 ставит в соответствие элемент
ставит в соответствие элемент 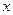 множества
множества 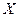 , связанный с
, связанный с  равенством
равенством 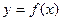 , называется обратной по отношению к
, называется обратной по отношению к  и обозначается
и обозначается 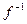 .
.
Очевидно  . Таким образом, можно говорить о паре взаимно обратных функций.
. Таким образом, можно говорить о паре взаимно обратных функций.
Определение 6. Пусть 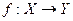 ,
, 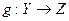 . Функция
. Функция 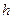 , определяемая равенством
, определяемая равенством
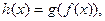
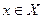 ,
,
называется сложной функцией, или суперпозицией функций  и
и  .
.
Определение 7. Пусть 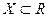 ,
, 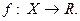 Функция
Функция  называется:
называется:
1) четной, если ее область определения 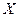 с каждой своей точкой
с каждой своей точкой 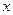 содержит
содержит 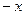 , и при этом
, и при этом 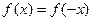 ;
;
2) нечетной, если ее область определения 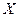 с каждой своей точкой
с каждой своей точкой 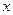 содержит
содержит 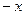 , и при этом
, и при этом 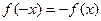 ;
;
3) периодической, если найдется 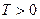 , такое что ее область определения
, такое что ее область определения 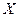 с каждой своей точкой
с каждой своей точкой 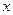 содержит точки
содержит точки  , и при этом
, и при этом  . Число
. Число 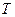 называется периодом функции
называется периодом функции  .
.
Если на плоскости ввести декартову систему координат  и каждую точку графика функции
и каждую точку графика функции  отождествить с точкой плоскости, координаты которой есть
отождествить с точкой плоскости, координаты которой есть 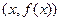 , то график четной функции будет симметричен относительно оси ординат, график нечетной функции– симметричен относительно начала координат, а графики взаимно обратных функций будут симметричны относительно прямой
, то график четной функции будет симметричен относительно оси ординат, график нечетной функции– симметричен относительно начала координат, а графики взаимно обратных функций будут симметричны относительно прямой  .
.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 317; Нарушение авторских прав?; Мы поможем в написании вашей работы!