Таким образом, функции

Непрерывность функции в точке.

Второй замечательный предел.

Можно показать, что

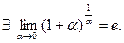
Это предельное соотношение называется вторым замечательным пределом.

Определение 1. Пусть 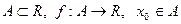-предельная точка множества 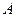. Говорят, что функция непрерывна в точке 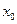, если 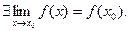Функция , непрерывная в каждой точке множества 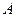, называется непрерывной на множестве .

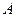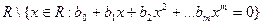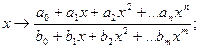
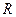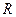э

э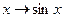

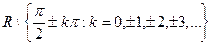э ;

э ;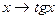

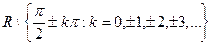э ;

э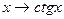

непрерывны в каждой точке своей области определения.

Предложение 1. Функция 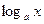непрерывна в каждой точке своей области определения.

Доказательство: Будем считать для определенности, что 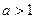. Для 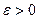подберем 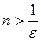и положим 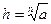. Очевидно 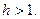Так как 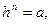то 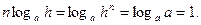Поэтому 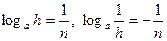. Таким образом, в промежутке 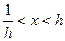выполняется неравенство 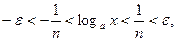что и доказывает непрерывность функции 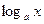в точке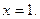

Пусть теперь 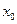– произвольное положительное число, 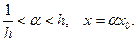Тогда

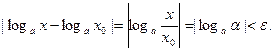
Так как интервал 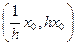включает в себя некоторый интервал 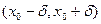, то это доказывает непрерывность функции 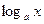в точке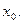

Используя второй замечательный предел, непрерывность функция 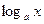и теорему о пределесложной функции, можно доказать, что:

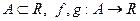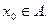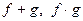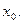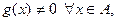Теорема 1. Пусть непрерывны в точке Тогда также непрерывны в точке Если то и 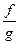непрерывна в точке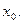

Теорема 2. Пусть 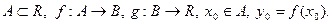Если непрерывна в в точке 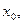а непрерывна в точке 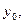то сложная функция 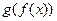непрерывна в точке .

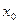15) Классификация точек разрыва.

Пусть 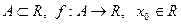– предельная точка множества 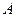(в ней функция вообще может быть не определена).

Определение 1. Говорят, что функция в точке 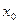терпит разрыв, если она в этой точке либо не определена, либо определена, но не является непрерывной.Точка 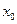разрыва функции называется:

1) точкой устранимого разрыва, если существует 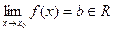, но либо функция в точке 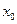не определена, либо 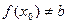(если положить 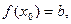то функция станет непрерывной в точке 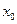, т.е. разрыв будет устранен);

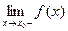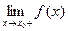2) точкой разрыва I рода, если существуют и конечны и , но

3)точкой разрыва II рода, если она не является точкой устранимого разрыва и точкой разрыва первого рода.

Пример 1. Пусть ,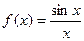

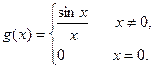
Для обеих этих функций точка 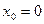является точкой устранимого разрыва. Пример2. Пусть

Для этой функции точка 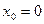является точкой разрыва первого рода.

Пример 3. Пусть 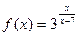. Для этой функции точка 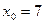является точкой разрыва II рода.

Дата добавления: 2014-11-06