
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции в точке
|
|
|
|
Последовательности.
Определение 1. Функцию, заданную на множестве натуральных чисел 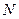 , называют последовательностью.
, называют последовательностью.
Значения такой функции обозначают 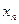 (или
(или  ) и называют членами последовательности, число
) и называют членами последовательности, число 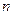 называют номером члена
называют номером члена 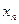 . Последовательность обозначают
. Последовательность обозначают
 или
или 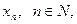 или
или 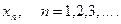
Последовательность, множество значений которой состоит из одного элемента, называют стационарной.
Последовательность может быть задана с помощью формулы вида

 ,
,
выражающей 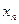 через номер
через номер 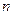 , например,
, например,
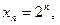
 ;
;
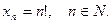
Такую формулу называют формулой общего члена последовательности. Для задания последовательности используют и рекуррентные формулы, т.е. формулы, выражающие 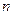 -ый член последовательности через члены последовательности с меньшими номерами (предыдущие члены).
-ый член последовательности через члены последовательности с меньшими номерами (предыдущие члены).
Определение 1. Под окрестностью символа - 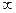 будем понимать множество вида
будем понимать множество вида
 |
 , где
, где 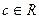 .
.
 |
Под окрестностью вещественного числа
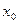 будем понимать множество вида
будем понимать множество вида  , где
, где 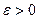 .
.
Под окрестностью символа + 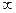 будем понимать множество вида
будем понимать множество вида  , где
, где 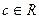 .
.

Окрестность точки 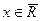 будем обозначать
будем обозначать 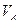 . Множество
. Множество  будем называть проколотой окрестностью точки
будем называть проколотой окрестностью точки 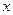 . Очевидно
. Очевидно 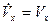 , если
, если  или
или 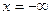 .
.
Свойства системы окрестностей точки.
1) Если 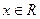 , то
, то 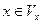 ;
;
2) Если 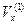 и
и  — две окрестности точки
— две окрестности точки 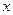 , то
, то 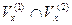 также есть окрестность точки
также есть окрестность точки 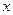 . Вообще, пересечение конечного множества окрестностей точки
. Вообще, пересечение конечного множества окрестностей точки 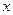 есть окрестность точки
есть окрестность точки 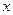 ;
; 
3) Если  , то
, то 
4) Существует убывающая последовательность 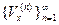 окрестностей точки
окрестностей точки 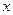 такая, что:
такая, что:
4.1) 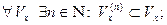
4.2) 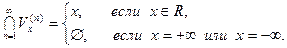
Действительно, если  , то полагаем
, то полагаем 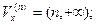 если
если  то полагаем
то полагаем  если
если 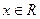 , то полагаем
, то полагаем 
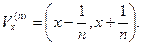
5) Если  , то
, то  и
и 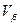 такие, что
такие, что 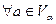 и
и  справедливо неравенство
справедливо неравенство 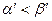 .
.
Все свойства предельного перехода обусловлены этими свойствами окрестностей.
Определение 2. Пусть 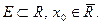 . Точка
. Точка 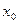 называется предельной точкой (точкой сгущения) множества E, если
называется предельной точкой (точкой сгущения) множества E, если  для любой окрестности
для любой окрестности  точки
точки 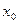 .
.
Смысл этого определения заключается в следующем: в любой окрестности точки 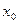 найдется элемент множества E, отличный от
найдется элемент множества E, отличный от 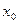 . Раскроим это определение:
. Раскроим это определение:
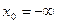 –предельная точка множества E, если E
–предельная точка множества E, если E 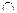 (-
(- 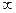 ,
,  )
) 
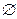 для
для 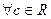 ;
;
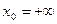 –предельная точка множества E, если E
–предельная точка множества E, если E 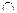 (
( ,+
,+ 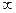 )
) 
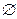 для
для 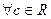 ;
;
 –предельная точка множества E, если
–предельная точка множества E, если  для
для 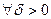 .
.
Пример 1. Пусть  . Тогда множество предельных точек
. Тогда множество предельных точек 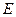 есть
есть 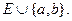
Пример 2. Единственной предельной точкоймножества натуральных чисел 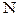 является
является 
Определение 3. Пусть 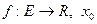 – предельная точка множества
– предельная точка множества 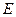 . Мы будем называть
. Мы будем называть 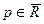 пределом функции
пределом функции  в точке
в точке 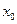 и писать
и писать  , или
, или  , если для любой окрестности
, если для любой окрестности 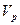 точки
точки 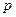 найдется такая окрестность
найдется такая окрестность  точки
точки 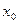 , что
, что 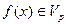 лишь только
лишь только 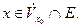 .
.
Запишем это определение символами:
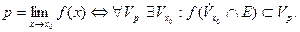
Говоря о пределе последовательности 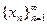 , принято писать
, принято писать  , или
, или  , опуская знак ”+” перед символом
, опуская знак ”+” перед символом 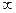 .
.
Конкретизируем понятие предела функции в точке:
1)  Тогда
Тогда

2)  Тогда
Тогда
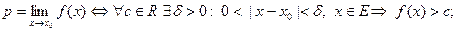
3)  Тогда
Тогда
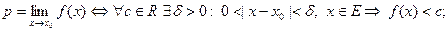
4)  Тогда
Тогда
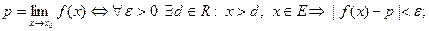
5)  Тогда
Тогда
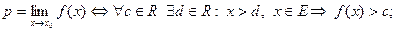
6) 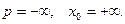 Тогда
Тогда

7) 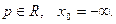 Тогда
Тогда
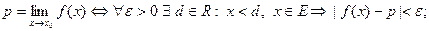
8)  Тогда
Тогда


9) 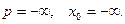 Тогда
Тогда
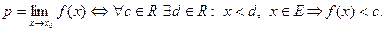
Для последовательностей равенство  означает следующее:
означает следующее:  лишь только
лишь только 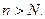
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 351; Нарушение авторских прав?; Мы поможем в написании вашей работы!