Линейные однородные уравнения n-го порядка

Дифференциальное уравнение называется линейным, если оно имеет вид

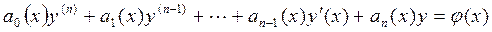. (1) Если 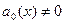, то путем деления на 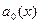оно может быть приведено к виду

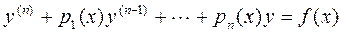. (1')

Если правая часть (1) тождественно равна нулю, то уравнение называется однородным линейным дифференциальным уравнением (ОЛДУ), в противном случае – неоднородным линейным дифференциальным уравнением (НЛДУ).

Если все и 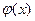непрерывны на интервале 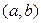и 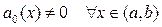, то для уравнения (1'), эквивалентного (1), выполнены все условия теоремы существования и единственности. Поэтому в окрестности любой точки 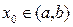, при любых 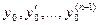существует решение уравнения (1), удовлетворяющее начальным условиям.

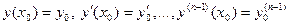. (2)

На самом деле можно показать, что решение существует не только в окрестности точки x₀, а на всем интервале .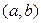

Положим 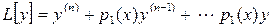. Тогда уравнение (1') можно записать в виде 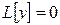. Очевидно 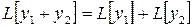, 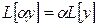. Поэтому имеет место следующая

Теорема 1. Пусть 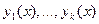– решения ОЛДУ (1'), –

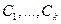произвольные постоянные. Тогда

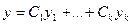(3)

так же есть решение ОЛДУ (1').

Вопрос о том, каким условиям должны удовлетворять частные решения 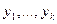уравнения (1'), чтобы формула (3) давала общее решение уравнения (1'), решается в связи с понятием линейной зависимости функций.

Определение 1. Функции 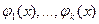, заданные на интервале (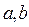), называются линейно независимыми на интервале 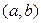, если .

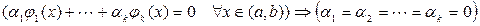В противном случае функции 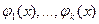называются линейно зависимыми.

Пример 1. 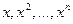есть линейно независимая система функций на любом интервале .

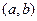Пусть мы имеем 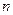функций 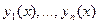, имеющих на интервале 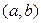непрерывные производные до порядка 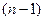включительно. Определитель

называется определителем Вронского (вронскианом) этих функций.

Теорема 2. Если функции 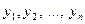линейно зависимы на 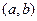, то .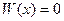

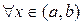Теорема 3. Если решения 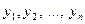уравнения (1') линейно независимы на 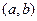, то .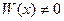

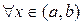Определение 4. Любая система из 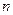линейно независимых частных решений ОЛДУ (1') называется фундаментальной системой.

Теорема 4. Любое ОЛДУ 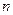- го порядка имеет фундаментальную систему решений.

Доказательство. Мы говорили выше, что задача Коши для (1') имеет решение при любом выборе начальных условий. Зафиксируем точку 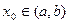и рассмотрим решения 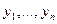задачи (1'), удовлетворяющие следующим начальным данным:

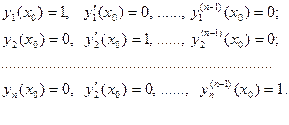
Пусть 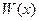– определитель Вронского системы функций 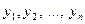. Тогда

,

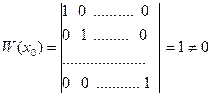и, тем самым, по Теореме 2 функции 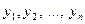линейно независимы.

Теорема 5 (О структуре общего решения ОЛДУ). Е сли 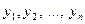образуют фундаментальную систему решений уравнения (1'), то его общее решение задается формулой

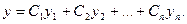(4)

Дата добавления: 2014-11-06