
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения первого порядка
|
|
|
|
Дифференциальные уравнения 1-го порядка имеют вид
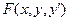 =0 или
=0 или 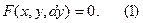
Если уравнение (1) удастся разрешить относительно 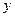 , то мы получим
, то мы получим
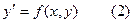
- уравнение первого порядка, разрешенное относительно производной.
Будем считать, что функция 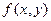 задана на некотором открытом множестве
задана на некотором открытом множестве 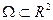 .
.
Общим решением дифференциального уравнения (2) называется функция
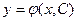 такая, что:
такая, что:
1) она удовлетворяет уравнению (2) при значениях постоянной  , принадлежащих некоторому определенному множеству; (это множество определяется уравнением (2)).
, принадлежащих некоторому определенному множеству; (это множество определяется уравнением (2)).
2) какова бы ни была точка 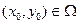 , найдется такое значение
, найдется такое значение 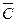 постоянной
постоянной  , что функция
, что функция 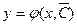 будет удовлетворять условию
будет удовлетворять условию 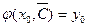 .
.
Соотношение вида 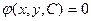 , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.
, неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.
Соотношение, получаемое из общего интеграла при конкретном значении постоянной  , называется частным интегралом дифференциального уравнения.
, называется частным интегралом дифференциального уравнения.
Имеет место следующая теорема существования и единственности решения дифференциального уравнения (2).
Теорема 1. Пусть функция 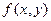 определена и непрерывна на открытом множестве
определена и непрерывна на открытом множестве 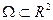 ,
, 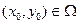 . Тогда через точку
. Тогда через точку 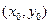 проходит по крайне мере одна интегральная кривая. Если функция
проходит по крайне мере одна интегральная кривая. Если функция 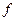 имеет на
имеет на  непрерывную частную производную
непрерывную частную производную 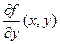 по переменной
по переменной 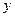 , то существует единственное решение
, то существует единственное решение 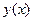 уравнения (2), удовлетворяющее условию
уравнения (2), удовлетворяющее условию 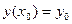 .
.
Условие 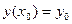 называют начальным условием. Задачу отыскания решения уравнения (2), удовлетворяющего начальному условию
называют начальным условием. Задачу отыскания решения уравнения (2), удовлетворяющего начальному условию 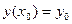 , называют задачей Коши.
, называют задачей Коши.
Единственность решения задачи Коши надо понимать в том смысле, что если 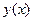 и
и 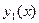 есть два решения задачи Коши, удовлетворяющие одному и тому же начальному условию
есть два решения задачи Коши, удовлетворяющие одному и тому же начальному условию 
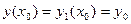 , заданные соответственно на интервалах
, заданные соответственно на интервалах 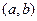 и
и 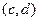 , то
, то 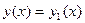 на пересечении этих интервалов.
на пересечении этих интервалов.
Уравнение (2) в каждой точке  определяет
определяет 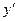 , то есть угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Поэтому задача интегрирования дифференциального уравнения (2) геометрически может быть истолкована следующим образом: от каждой точки
, то есть угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Поэтому задача интегрирования дифференциального уравнения (2) геометрически может быть истолкована следующим образом: от каждой точки  отложим вектор, образующий с осью
отложим вектор, образующий с осью 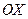 угол
угол 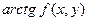 ; получим некоторое поле направлений; требуется провести кривые так, чтобы расставленные стрелки показывали в каждой точке направление касательной.
; получим некоторое поле направлений; требуется провести кривые так, чтобы расставленные стрелки показывали в каждой точке направление касательной.
Изоклиной дифференциального уравнения (2) называется геометрическое место точек, в которых касательные к интегральным кривым имеют одно и то же направление.
Семейство изоклин определяется уравнением 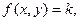 где
где 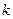 – параметр. Строя достаточно густую сеть изоклин, т.е. давая
– параметр. Строя достаточно густую сеть изоклин, т.е. давая 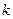 близкие числовые значения, мы можем достаточно точно построить интегральную кривую
близкие числовые значения, мы можем достаточно точно построить интегральную кривую
дифференциального уравнения (2).
Не существует общего метода решения дифференциального уравнения первого порядка. Далее мы выделим некоторые типы дифференциальных уравнений, для которых можно дать метод решения.
4) Уравнения с раздельными и разделяющимися переменными.
Дифференциальное уравнение вида
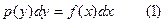
называется уравнением с разделенными переменными.
Дифференциальное уравнение вида
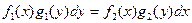 (2)
(2)
называется уравнением с разделяющимися переменными.
Путем деления на 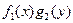 , оно приводится к дифференциальному уравнению
, оно приводится к дифференциальному уравнению
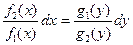 ,
,
которое имеет вид (1).
Будем считать в (1) 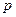 и
и 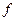 – непрерывными функциями, а
– непрерывными функциями, а 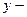 функцией независимого переменного
функцией независимого переменного  . Выражение
. Выражение 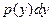 слева есть дифференциал некоторой функции
слева есть дифференциал некоторой функции  , зависящей от
, зависящей от 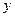 , а выражение
, а выражение 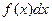 справа – дифференциал некоторой функции
справа – дифференциал некоторой функции 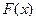 , зависящей от
, зависящей от 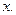 Решениями дифференциального равнения (1) будут те и только те дифференцируемые функции
Решениями дифференциального равнения (1) будут те и только те дифференцируемые функции 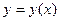 , которые при некоторой постоянной
, которые при некоторой постоянной  удовлетворяют уравнению
удовлетворяют уравнению 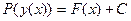 . При этом следует помнить, что если
. При этом следует помнить, что если 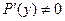 , то по теореме о неявной функции функция
, то по теореме о неявной функции функция 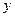 , определяемая неявно уравнением
, определяемая неявно уравнением 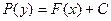 , где
, где  – произвольная постоянная, будет дифференцируемой.
– произвольная постоянная, будет дифференцируемой.
Пример 1. Решить дифференциальное уравнение
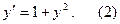
Решение. Разделим в (2) переменные и придем к уравнению
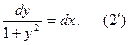
Решением дифференциального равнения (2) будет функция 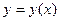 такая, что
такая, что 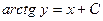 , где
, где  – произвольная постоянная. Отсюда
– произвольная постоянная. Отсюда 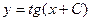 .
.
Пример 2. Решить дифференциальное уравнение
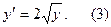
Решение. Очевидно, функция 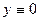 есть решение уравнения (3). Пусть теперь y>0. Разделим в (3) переменные и придем к уравнению
есть решение уравнения (3). Пусть теперь y>0. Разделим в (3) переменные и придем к уравнению
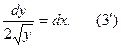
Проинтегрировав (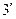 ), получим
), получим  где
где  – произвольная постоянная. Отсюда следует, что
– произвольная постоянная. Отсюда следует, что 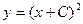 ,
, 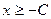 . Таким образом, при каждом фиксированном значении
. Таким образом, при каждом фиксированном значении  функция
функция 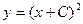 ,
, 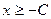 является решением уравнения (3). Других решений это уравнение в полуплоскости
является решением уравнения (3). Других решений это уравнение в полуплоскости 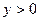 не имеет.
не имеет.
Пример 3. Проинтегрировать уравнение
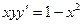 (4)
(4)
Решение. В этом уравнении переменная  не может принимать значение 0. Поэтому возможно деление на
не может принимать значение 0. Поэтому возможно деление на  . Разделив в (4) переменные, получим
. Разделив в (4) переменные, получим
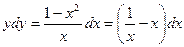 . (
. (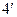 )
)
Проинтегрировав (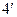 ), имеем
), имеем 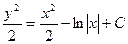 , или
, или 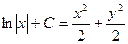 . Постоянную
. Постоянную  запишем в виде
запишем в виде  .Тогда
.Тогда 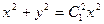 . Введем постоянную
. Введем постоянную 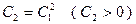 . Тогда общий интеграл уравнения (4) есть
. Тогда общий интеграл уравнения (4) есть
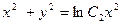 .
.
В общем интеграле дифференциального уравнения первого порядка одна произвольная постоянная, которую принято обозначать как  . По этой причине принято при переходе от одной произвольной постоянной к другой, например, от
. По этой причине принято при переходе от одной произвольной постоянной к другой, например, от  к
к 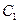 от
от 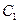 к
к 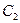 , индексы не записывать. Следовательно, общий интеграл уравнения (4) имеет вид
, индексы не записывать. Следовательно, общий интеграл уравнения (4) имеет вид
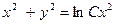 (С> 0).
(С> 0).
Пример 5. Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию.
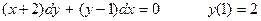 (5)
(5)
Решение. Мы ищем решение 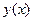 дифференциального уравнения (5) в окрестности точки
дифференциального уравнения (5) в окрестности точки  , удовлетворяющее условию
, удовлетворяющее условию 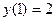 . Дифференцируемая функция
. Дифференцируемая функция
непрерывна. Поэтому окрестность точки  будем считать столь малой, что
будем считать столь малой, что
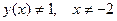 (6)
(6)
для любого  из этой окрестности. Тогда
из этой окрестности. Тогда 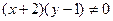 . Разделив на
. Разделив на 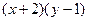 , получим
, получим 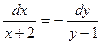 , откуда
, откуда
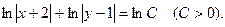
Следовательно, с учетом (6), общий интеграл данного уравнения есть
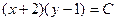 (С>0).
(С>0).
Найдем значение параметра  , которому соответствует кривая, удовлетворяющая начальному условию
, которому соответствует кривая, удовлетворяющая начальному условию 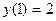 , то есть проходящая через точку (1,2)
, то есть проходящая через точку (1,2) 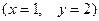 :
:
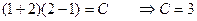
Таким образом, решением будет 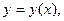 такое, что
такое, что 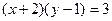 .
.
Пример 6. Проинтегрировать уравнение
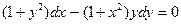
Решение.
Разделив на 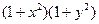 , получим
, получим
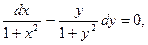
откуда
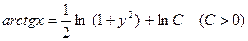 , или
, или 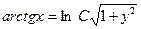 .
.
Дифференциальное уравнение
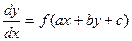
приводится к уравнению с разделяющимися переменными подстановкой 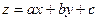 . Действительно,
. Действительно, 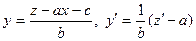 . Следовательно
. Следовательно
 , или
, или 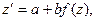 откуда
откуда 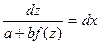 .
.
Дифференциальное уравнение
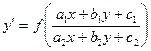
приводится к уравнению с разделяющимися переменными, если 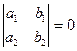 . Действительно, в этом случае
. Действительно, в этом случае 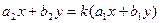 при некотором
при некотором 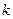 . Следовательно, дифференциальное уравнение может быть записано в виде
. Следовательно, дифференциальное уравнение может быть записано в виде
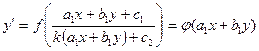 ,
,
и по предыдущему подстановкой 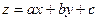 оно может быть приведено к уравнению с разделяющимися переменными.
оно может быть приведено к уравнению с разделяющимися переменными.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 374; Нарушение авторских прав?; Мы поможем в написании вашей работы!