Стандарт ІЕЕЕ-754

Для представлення чисел з рухомою комою у більшості сучасних комп’ютерів ви­користовується стандарт ІЕЕЕ-754. В попередньому пункті ми розглянули можливі варі­анти представлення даних в форматі з рухомою комою. До середини 80-х років в різних комп’ютерах використовувались різні варіанти цього представлення, що суттєво усклад­нювало виконання на них тих самих програм. У 1985 році Інститут інженерів електро­техніків і радіоелектроніків (ІЕЕЕ) розробив стандарт для чисел з рухомою комою, який офіційно відомий як ІЕЕЕ-754 (1985).

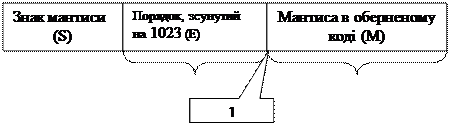
Стандарт ІЕЕЕ-754 для чисел з одинарною точністю використовує зміщення 8-роз- рядного порядку на 127. Це ще один спосіб представлення чисел із знаком без викорис­тання знаку мінус. Мантиса має 23 біти. Із знаковим розрядом включно повна довжина слова складає 32 біти (рис. 2.13).

0 1 8 9 31

Знак мантиси (S)

Мантиса в оберненому коді (М)

Порядок, зсунутий на 127 (Е)

8 бітів 23 біти

Рис. 2.13. ІЕЕЕ-754 стандарт для чисел з одинарною точністю

Значення числа обчислюється за формулою:

число = (-1)^s 2^Е-127 (1, М).

Мантиса представляється в прямому коді без знаку, знак мантиси представляється окремо. Суть нормалізації полягає в тому, що мантиса приводиться до вигляду 1.ххххх, тобто вона знаходиться в межах від 1,000...0 до 1,111...1. Слід зауважити, що оскільки кожна мантиса після нормалізації починається з 1, то нема сенсу зберігати цей розряд, тому він не зберігається разом з числом. Його необхідно просто враховувати під час операцій над числами.

Числа з подвійною точністю в стандарті ІЕЕЕ-754 подаються 64-розрядним словом, яке має знаковий розряд, 11-розрядний порядок і 52-розрядну мантису (рис. 2.14). Змі­щення порядку дорівнює 1023.

0 1 11 12 63

11 бітів 52 біти

Рис. 2.14. ІЕЕЕ-754 стандарт для чисел з подвійною точністю

Значення числа обчислюється за формулою:

число = (-1)^s • 2^Е-1023 (1, М).

Діапазон чисел, які можуть бути представлені в цьому форматі, показаний на рис. 2.15.

Рис. 2.15. Діапазон чисел, які відображаються у форматі за стандартом ІЕЕЕ-754

з подвійною точністю

У табл. 2.6 наведено характеристики форматів подання двійкових чисел в стандарті ІЕЕЕ-754 з одинарною та подвійною точністю.

Таблиця 2.6

Характеристика	Формат з одинарною точністю	Формат з подвійною точністю
Довжина слова	32 біти	64 біти
Мантиса (зі знаком)	24 біти	53 біти
Порядок	8 бітів	11 бітів
Зміщення
Наближений діапазон	2^128 = 3.8 1 0^38	2^1024= 9 10^307
Найменше нормалізоване число	2-126 = 10-зз	2-1022 _ Ю"^308
Наближена точність представлення чисел	2'^23= 10-^7	2‘^52= 10-^15

Як числа з одинарною точністю, так і числа з подвійною точністю в стандарті ІЕЕЕ-754 мають для нуля два варіанти представлення. Коли порядок і мантиса рівні нулю - число є нулем. При цьому значення знаку є несуттєвим. На цю обставину потрібно звертати увагу при проведенні операції порівняння числа з рухомою комою на збіжність з нулем.

Стандарт ІЕЕЕ-754 передбачає використання певної кількості значень мантиси та порядку для представлення нескінчених, невизначених та малих значень. Так мінус та плюс нескінченість пода'ються максимальним значенням порядку (З77₈ для числа з одинарною точністю та 3777_g для числа з подвійною точністю) та нульовою мантисою. Для представлення невизначеного значення також використовується максимальне значення порядку та ненульова мантиса. Невизначене значення називають “не числом” - Not a Nu­mber (NaN). “Не число” використовується, щоб представити значення, яке не є дійсним числом і часто використовується як індикатор помилки, наприклад, коли відбулося ді­лення 0 на 0. Якщо число є дуже малим, то воно представляється нульовим порядком та ненульовою мантисою. У табл. 2.7 наведено приклади представлення різних величин в форматі за стандартом ІЕЕЕ-754 для чисел з одинарною та подвійною точністю.

Таблиця 2.7

	32-розрядні числа	64-розрядні числа
Приклади	Знак	Порядок	Мантиса	Знак	Порядок	Мантиса
NaN	?	377,	Не нуль		3777,	Не нуль
+ нескінченість		377,	.00000000,		37778	.000000000000000000,
10,0		2028	(1).20000000,		20028	(1).0400000000000000008
1,0		177s	(1).000000008		1777,	(1).000000000000000000000008
0,0		ооо8	.00000000,		0000,	.0000000000000000008
Ненормалізоване		0008	Не нуль		оооо8	Не нуль
-0,0		ооо8	•000000008		0000,	•0000000000000000008
-1,0		1778	(І).ОООООООО,		1777,	(1).0000000000000000000008
-10,0		202,	(1).20000000,		2002,	(1).0400000000000000008
- нескінченість		3778	.00000000,		37778	.0000000000000000008

Тут знаком? позначено несуттєве значення, а (1) - значення, яке не зафіксовується елементами пам’яті комп’ютера.

Дата добавления: 2014-11-06