Исследование методов инженерного расчета АТКЧ

ИССЛЕДОВАНИЕ ТОКОВ КОМБИНАЦИОННЫХ ЧАСТОТ В ПРЕОБРАЗОВАТЕЛЯХ ЧАСТОТЫ РРС

Лабораторная работа 2

Отчет

Отчет должен содержать распечатки:

1. Результатов расчета ВАХ.

2. Данных аппроксимации ВАХ.

3. Производных ВАХ по напряжению.

Выводы и сравнительный анализ производных по напряжению и их величин в зависимости от порядка производной

2.1. Цель занятий.

Исследование способов инженерного расчета АТКЧ в ПРЧ при использовании ПМ и АФ, рассмотренных в ЛР 1, и программ для их расчета. Расчет интеграла (1.15) для рабочего режима смесительного диода и подготовка данных для расчета допустимой мощности помех на входе ПРЧ в ЛР 4.

В ЛР 1 были рассмотрены 3АФ для расчета АТКЧ с использованием прямой и обратной АФ. Как следует из (1.10) основную сложность определения АТКЧ вызывает расчет интеграла (1.15). В наиболее простой экспоненциальной АФ проблема расчета решается использованием МФБ. Однако недостаточная точность Ар ВАХ экспонентой и качественные различия характера изменений ее производных по напряжению от производных реальных ВАХ могут вызывать сомнения в целесообразности ее использования. Наибольшую точность обеспечивает экспоненциальная АФ (1.19), учитывающая сопротивление слоя полупроводника. Но это усложняет расчет, т.к. необходимо использование обратной функции. Задача решается ПМИ методом суммирования большого количества прямоугольников согласно [8] при задании одинакового шага. На следующей странице приводится программа расчета (1.15) с использованием обратной функции в виде логарифмической функции и особенности расчета, которые потом будут применены для (1.19). Там же приведена методика расчета для другой АФ (1.33) при использовании ПМ. Отметим, что для расчета АТКЧ при использовании (1.33) могут быть применены аналитические методы расчета, приводящие к использованию комплексной переменной и методов теории вычетов. Получаемые формулы громоздки [10] и требуют больших затрат времени на расчеты и их проверку.

Оценим результаты использования ПМИ при применении экспоненциальной АФ и ее обратной логарифмической, т.к они позволяют оценить возможные погрешности расчета сопоставлением их с данными, которые вытекают непосредственно из данных расчета МФБ в соответствии с программой, приведенной в Приложении 2.1 на упрощенной модели, которая подготавливает разработку методик инженерных расчетов в разделах 2.2.2 и 2.2.3. В качестве модели в программе используется функция

r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> (2.1)

где (2.2)

Т – фаза, которая моделирует фазу напряжения гетеродина в (1.15).

Для расчета половинных значений амплитуд m гармоник согласно интеграла (1.15) при использовании (2.1) в интервале от 0 заменим интеграл дискретным суммированием прямоугольников, применив ПМИ [8]

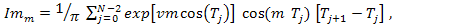(2.3)

где N- количество точек расчета,

- дискретные значения фаз, (2.4)

-интервал дискретизации фаз. (2.5)

Из (2.3) следует, что разность 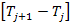=s постоянна по величине и выносится за знак суммы. После преобразований (2.3) с учетом (2.5) получим

(2.6)

которое использовано в программе вышеупомянутого приложения для сравнительного анализа с другими возможными методами расчета.

При моделировании использования обратной АФ применим вытекающая из (2.1) функцию

(2.7)

В этом случае отсутствует возможность проводить вычисления с применявшимся в (2.6) постоянным интервалом суммирования по фазе. Тогда может быть использован постоянный интервал по току согласно равенству:

(2.8)

где - интервал дискретизации суммируемых токов, (2.9)

im- максимальный величина тока, соответствующая подаче на смесительный диод напряжения, соответствующего амплитуде напряжения гетеродина.

Из (2.1) и (2.2) значение 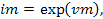которое для задаваемого в программе значения максимального значения im =1000 соответствует vm = 6.908. Подставляя (2.2) в (2.7) с учетом (2.8), получим следующее равенство:

(2.10)

из которого следует уравнение для определения значения фазы при суммировании:

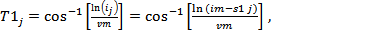(2.11)

где аналогично пояснениям к (1.32) = arccos.

(2.11) предоставляет возможность записать следующее уравнение для расчета ПМИ половинных значений амплитуд m гармоник применительно обратной АФ, рассмотренной в Приложении 2.1:

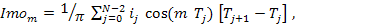(2.12)

где i_j определяется (2.8), а T_j – (2.11) аналогично тому, как производится в вышеупомянутой программе.

Аналогичный метод суммирования можно разработать для АФ при постоянном шаге изменения напряжения, а не фазы, рассмотренный в (2.6), задавшись следующим равенством для изменений напряжений:

(2.13)

где vm - максимальное напряжение, прикладываемое к диоду, которое соответствует амплитуде напряжения гетеродина

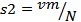-шаг изменения напряжения. (2.14)

Аналогично (2.10) подставляя задаваемые дискретные значения напряжений 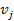согласно (2.13) в (2.2), получим равенство для определения соответствующих значений фаз синусоидального колебания:

(2.15)

из которого следует уравнение для определения меняющегося значения текущей фазы при суммировании:

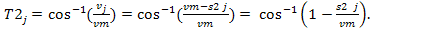(2.16)

(2.16) предоставляет возможность записать следующее уравнение для расчета ПМ половинных значений амплитуд m гармоник применительно АФ при постоянном шаге изменений напряжений:

(2.17)

которое с программе названа модифицированным.

Половинные значения амплитуд m гармоник применительно к экспоненциальной АФ можно получить согласно (1.16) непосредственно из разложения (2.1) в сумму МФБ, каждая из которых рассчитывается в Маткаде. В Приложении 2.1 она предствлена функцией In(m, vm), которая используется для проверки полученных ПМИ. Результаты расчета объединены в общую матрицу Ie. Номера столбцов в вышеупомянутой матрице соответствуют значениям m-номеров гармоник. Соответствие строк матрицы расчетным формулам вытекает из заданного в программе алгоритма объединений строк в матрицу, приводимое в таблице 2.1.

Табл. 2.1

№ строки
№ формулы	(2.6), прямая	(2.12), обр.	(2.17), модф.	МФБ

Сопоставление методов расчета показывает:

1. Расхождение их не превышает 1% для 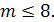Следовательно, в первом приближении метод может быть использован для расчета АТКЧ до такого же порядка при N=10000 за исключением модифицированного, где погрешность расчетов больше.

2. С увеличением m расхождение значений возрастает и, начиная с значения (1.15), практически не уменьшаются и даже начинает несколько расти в отличие от соответствующих МФБ, что требует в дальнейшем проведения дополнительных исследований или использования более совершенных ЭВМ, с помощью которых возможно будут получены лучшие результаты.

Дата добавления: 2014-11-06