Дифференциальные уравнения второго порядка с постоянными коэффициентами

Дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:

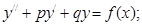
если в правой части уравнения стоит ноль, то

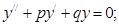
то уравнение называется однородным линейным.

Для решения такого уравнения составляется характеристическое уравнение. Характеристическим называется квадратное уравнение, полученное на основе дифференциального уравнения, в котором 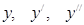заменяются новой переменной k, степень которой определяется порядком производной:

;

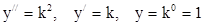Тогда 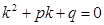- характеристическое уравнение.

Находим корни характеристического уравнения:

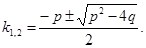
1. Если корни характеристического уравнения действительные и равные 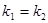, т.е. дескременант Д=0, то решением дифференциального уравнения будет являться функция:

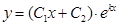. (1)

2. Если корни характеристического уравнения действительные и равные числа 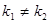, Д>0, то:

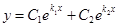. (2)

3. Если корни характеристического уравнения – комплексные числа при Д<0, т.е. 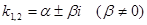, то

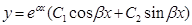. (3)

Например: Найти общее решение дифференциального уравнения:

1.

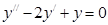
Составляем характеристическое уравнение:

;

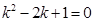Находим его корни:

;

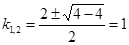k₁=k₂=k=1

Подставляем полученное значение к=1 равенство (1), получаем:

.

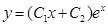2.

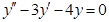
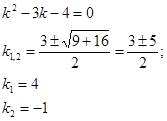
Полученные значения к₁ и к₂ подставляем в равенство (2), получаем:

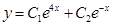
3.

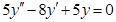
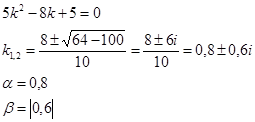
Полученные значения α и β подставляем в равенство (3), получаем:

5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА

Пусть у нас есть дифференциальное уравнение, разрешенное относительно второй производной:

,

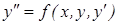Рассмотрим виды дифференциальных уравнений второго порядка, которые допускают понижение порядка:

I. Дифференциальные уравнения не содержащие аргумента:

(*)

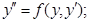Вводим новую переменную Р:

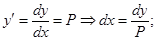
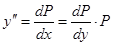подставляем это в (*) получаем:

.

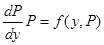Получили дифференциальные уравнения первого порядка и его решением будет функция: или

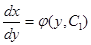Разделяем переменные, умножая обе части на :

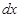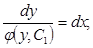
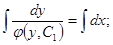
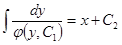- Общее решение

Пример:

.

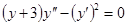Вводим замену: 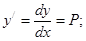(1)

Из равенства (1) получаем: 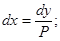(2)

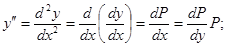Тогда (3)

Подставляем значения 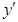и 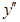из равенств (1) и (3) в заданное уравнение и получаем:

.

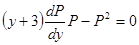Получили уравнение первого порядка. Решаем методом разделения переменными Р и у. Уравнение решается относительно Р.

.

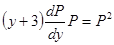Сокращаем обе части на Р

.

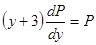Делим переменные, умножая обе части на 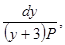получаем:

.

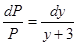Интегрируем оба части:

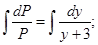
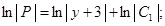
Потенцируем:

(4)

Подставляем полученное значение Р из равенства (4) в равенство (1), получаем:

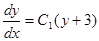
Вновь получили дифференциальное уравнение первого порядка относительно переменных у и х.

Делим переменные, умножая обе части равенства на 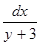, получаем:

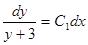
Интегрируем:

.

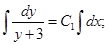
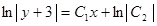Потенцируем:

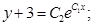
Получаем общее решение дифференциального уравнения:

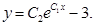
II. Дифференциальные уравнения не содержащие искомой функции:

(**)

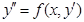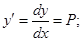
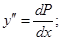
Тогда уравнение (**) примет вид:

.

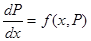Решением этого уравнения будет функция: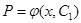

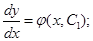
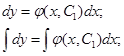
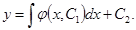- Общее решение

Пример:

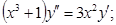
Вводим замену: 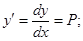(1)

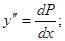Тогда (2)

Подставляем значения 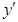и 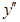из равенств (1) и (2) в исходное уравнение и получаем:

.

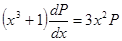Делим переменные, умножая обе части на 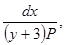получаем:

.

Интегрируем оба части равенства:

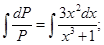
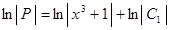
Потенцируем:

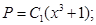(3)

Подставляем значение Р из равенства (3) в равенство (1) и получаем:

.

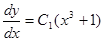Делим переменные, умножая обе части равенства на 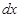, и интегрируем:

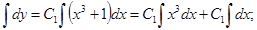
- Общее решение

III. Дифференциальные уравнения не содержащее искомой функции и её производной:

(***)

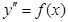Подстановка: 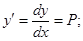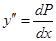подставляем в (***)

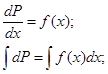
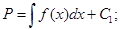
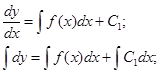
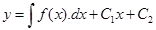- Общее решение

Например: Найти общее решение дифференциального уравнения:

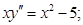
Вводим подстановку: 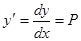(1)

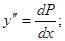Тогда (2)

Подставляем значения 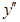из равенства (2) в исходное уравнение:

.

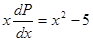Делим переменные, умножая обе части равенства на 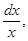получаем:

.

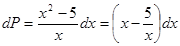Решаем полученное уравнение, интегрируя обе части:

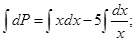
и получаем;

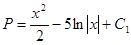(3)

Подставляем значение Р из равенства (3) в равенство (1), получаем:

.

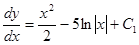Делим переменные, умножая обе части равенства на 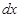, и интегрируем:

.

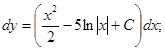
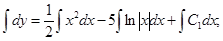
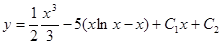Таким образом,

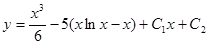- Общее решение

Примечание. Решаем интеграл 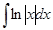методом интегрирования по частям:

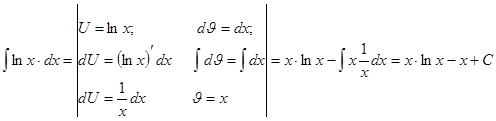
Дата добавления: 2014-10-15