Решение. Эталоны решения типовых задач

Эталоны решения типовых задач

Задача №1. Проводившиеся в некотором районе многолетние наблюдения показали, что из 50000 двадцатилетних граждан до 50 лет доживает в среднем 18120 человек, до 80 лет-724. Найти вероятности для двадцатилетних и пятидесятилетних дожить до 80 лет.

Дано: Решение:

n=50000 Вероятность дожить до 80 лет 20-летному гражданину Р(А₁)

m₁=18120 равна:

m₂=724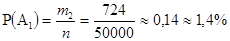

P(A₁)-? Вероятность дожить пятидесятилетному до 80 лет Р(А₂) равна:

P(A₂)-?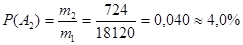

Ответ: P(A₁)=1,4% P(A₂)= 4%

Задача №2. Вероятность вызова врача в течение часа P(A)=0,47. Найти вероятность, что в течение часа вызова врача не последует.

Дано: Решение:

P(A)=0,47 Сумма вероятностей двух противоположных событий равна 1:

-?

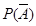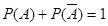
Отсюда:

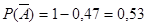
Ответ: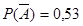

Задача №3. Аптечный склад получает лекарства из городов А,В,С и Д. Вероятность поступления лекарств из города А - Р(А)=0,11; из города В – Р(В)=0,28 и из города Д – Р(Д)=0,32. Найти вероятность поступления лекарств из города С.

Дано: Решение:

P(A)=0,11 Сумма вероятностей событий, составляющих полную

P(В)=0, 28 систему, равна единице (условие нормировки)

P(Д)=0,32 P(А)+P(В)+Р(С)+P(Д)=1

P(С)-? Р(С)=1-(Р(А)+Р(В)+Р(Д))=1-(0,11+0,28+0,32)=1-0,71=0,29

Ответ: Р(С)=0,29=29%

Задача №4. На обследование прибыла группа из 50 человек. Семеро из них больны. В кабинет врача приглашали по 2 человека. Найти вероятность того, что:

а) оба больны,

б) оба здоровы,

в) один болен, один здоров.

Дано: Решение:

n=50 а) Пусть Р(А) вероятность того, что первый

m=7 вошедший болен, а Р(В) – второй вошедший болен. Р(А и В)-? Р(А и В, или С и Д)-? События А и В зависимые.

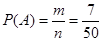
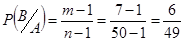
Р(А и В)=Р(А)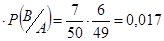

б) А - первый здоров, В -второй здоров.

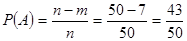
Р(А и В)=Р(А)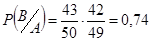

в) Первая ситуация:

А- первый болен, В - второй здоров

Р(А)=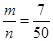

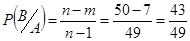
Р(А и В)=Р(А)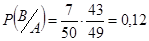

Вторая ситуация:

С- первый здоров, Д - второй болен

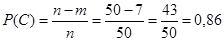
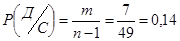
Р(С и Д)=Р(С)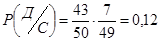

Общая вероятность равна:

Р(А и В, или С и Д)= Р(А и В)+ Р(С и Д)=0,12+0,12=0,24

Ответ: а. Р(А и В)=0,017

б. Р(А и В)=0,74

в. Р(А и В, или С и Д)=0,24

Задача №5. Из 20 ампул с лекарственными препаратами ёмкостью по 2 мл в 5 ампулах количество препарата отличалось от нормы. Какова вероятность, что из трёх наугад взятых ампул хотя бы одна окажется нестандартной?

Дано: Решение:

n=20 Задача решается от противного. Противоположными будут

m=5 события, что во всех трёх ампулах лекраственного препарата

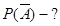содержится в норме (2мл).

Вероятность, что в первой ампуле содержится норма препарата:

;

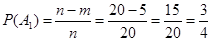во второй:

;

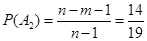в третьей:

.

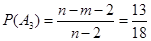Вероятность, что во всех трёх ампулах содержится норма лекраственного препарата:

Р(А)=Р(А₁ и А₂ и А₃)=Р(А₁)·Р(А₂)·Р(А₃)=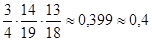

Сумма вероятностей противоположных событий равна единице

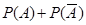=1

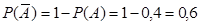
Ответ: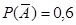

Дата добавления: 2014-10-15