Взаємодії. Закони динаміки точки

На минулій лекції ми познайомились із найпростішим видом руху – механічним, та розглянули деякі його закономірності. Проте, ми не торкались причин, які спричиняють рух тіла або змінюють його характер. Причинами ж зміни стану руху тіла є його взаємодія із навколишніми тілами. Одне із визначень фізики, як науки, таке: фізика є вченням про різні типи взаємодій – гравітаційну, електромагнітну, сильну і слабку. Перші два види відомі людям досить добре. Гравітаційна взаємодія утримує, наприклад, планети при їх русі навколо зірок. Електромагнітна взаємодія утримує електрони, що обертаються навколо атомних ядер, і є основним між атомами і молекулами. Електромагнітні і гравітаційні взаємодії проявляють себе у макро- і мегасвіті, змінюються із відстанню, як 1/ r ² та є далекодіючими – радіус їхньої дії необмежений. Дві останні взаємодії вимагають спеціальних методів дослідження. Сильні взаємодії – ядерні, зв'язують нуклони (протони і нейтрони) у ядрах хімічних елементів, а також утримують кварки усередині протону. Найбільші відстані, на яких виявляються сильні взаємодії (радіус їхньої дії) складає ~10^{-15 м. Слабкі взаємодії відповідальні за всі види} b -розпаду нейтронів ядер, за багато процесів розпаду елементарних частинок, а також за всі процеси взаємодії нейтрино із речовиною. Слабкі взаємодії, як і сильні, є ще більш короткодіючими, радіус дії яких складає всього ~10^{-17 м.}

Для характеристики ступеня взаємодії тіл у фізиці вводиться фізична величина, звана силою. Сила – векторна фізична величина, яка служить мірою механічної дії на розглядуване тіло з боку інших навколишніх тіл або полів, в результаті якого тіло або змінює своє положення у просторі, або змінює свою форму і розміри. У будь-який момент часу сила характеризується числовим значенням (модулем), напрямом у просторі і точкою прикладання. Вимірюється сила величиною пружної деформації, а одиницею виміру сили служить Ньютон (Н). Розділ механіки, присвячений вивченню руху матеріальних тіл під дією прикладених до них сил, називають динамікою. У основі класичної динаміки – наукипро рух тіл – лежать три закони Ньютона, тому її часто називають ньютонівською. Закони сформульовані ним у 1667 році у роботі «Математичні засади натуральної філософії» і виявились узагальненням численних дослідних даних.

Оскільки взаємодія тіл припускає дію першого тіла на друге і другого на перше одночасно, то сила характеризує обидві дії разом, тому зображається двома стрілками, прикладеними до обох тіл і спрямованими у протилежні сторони. Природно, що сили взаємодії між тілами мають однакову природу, завжди виникають парами і прикладені до різних (взаємодіючих) тіл. Це твердження про взаємність механічної дії тіл одне на одного у фізиці носить назву третього закону Ньютона, який формулюється так: при взаємодії двох тіла вони діють одне на одного силами, які мають однакову природу, спрямованими уздовж однієї прямої, рівними за величиною та протилежними за напрямком:

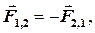(2.1)

де F _1,2 –сила, яка діє на перше тіло з боку другого, а F _2,1 – сила, яка діє на друге тіло з боку першого. Прикладені ці сили до різних тіл, тому вони не врівноважують одна одну. Взаємодії, що розглядаються законом, можуть бути як прямими або контактними (наприклад, при зіткненні тіл), так і непрямими або діями на відстані (наприклад, притягання Сонця і Землі). Цей закон дозволяє здійснити перехід від динаміки окремої матеріальної точки до динаміки системи точок, які взаємодіють попарно одна із одною.

Другий закон Ньютона називають основним законом динаміки, оскільки він встановлює зв'язок між динамічними і кінематичними величинами. Окрім сили, іншою найважливішою динамічною характеристикою тіла служить його маса. Маса тіла – скалярна фізична величина, яка є однією із основних характеристик матерії і визначає її інерційні (інертна маса) і гравітаційні (гравітаційна маса) властивості, а також її енерговміст. Інертністю тіла називається властивість, притаманна всім тілам і полягає у тому, що тіла чинять опір зміні своєї швидкості (і за модулем, і за напрямком). Особливості гравітаційних взаємодій визначаються законом Всесвітнього тяжіння і будуть розглянуті пізніше. У наш час можна вважати доведеним, що інертні і гравітаційні маси дорівнюють одна одній (з точністю, не меншою за 10^-12 їхнього значення). Маса є адитивною величиною: маса складеного тіла дорівнює сумі мас його частин. В межах класичної механіки, маса тіла є сталою величиною – не змінюється при його русі (зі швидкостями V<<c). Одиниця виміру маси – кілограм (кг). Другий закон Ньютона формулюється так: прискорення, якого набуває матеріальна точка (тіло), пропорційне прикладеній до нього силі, співпадає із нею за напрямом і обернено пропорційне масі цієї матеріальної точки (тіла):

(2.2)

У фізиці справедливий принцип незалежності дії сил: якщо на матеріальну точку (тіло) діє одночасно декілька сил, то кожна із них надає точці прискорення, визначуване другим законом Ньютона, незалежно від дії решти сил. Тому прискорення, якого набуде точка під дією декількох сил, визначається співвідношенням:

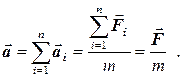(2.3)

Тут 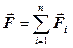- результуюча сила – геометрична сума всіх прикладених сил. Сила завжди може бути розкладена на дві складові – тангенціальну F_t і нормальну F_n: 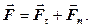Розкладання результуючої сили на складові приводить до істотного спрощення вирішення задач. Наприклад, якщо на рисунку діючу сила F= m× а розікласти на два компоненти: тангенціальну силу F_t (спрямовану по дотичній до траєкторії) і нормальну силу F_n (спрямовану по нормалі до траєкторії, до центру кривини), то модулі цих складових визначаються співвідношеннями:

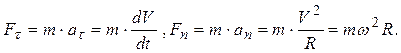(2.4)

Самим Ньютоном другий закон динаміки був сформульований не через прискорення, а через імпульс тіла. Імпульсом матеріальної точки (тіла) називають векторну фізичну величину, чисельно рівну добутку маси матеріальної точки (тіла) на її швидкість, напрям якої збігається із напрямом швидкості: p= m× V. Одиниця виміру імпульсу – кілограм-метр за секунду (кг×м/с). Використовуючи визначення прискорення точки і визначення імпульсу, одержимо авторський вираз і формулювання другого закону Ньютона:

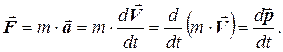(2.5)

Ця формула висловлює другий закон Ньютона у найзагальнішій формі, коли і маса рухомого тіла може змінюватись із часом: швидкість зміни імпульсу матеріальної точки (тіла) дорівнює діючій на неї (нього) силі і відбувається у напрямку дії сили. Записане рівняння ще називають рівнянням руху матеріальної точки.

Перший закон Ньютона називається законом інерції. У формулюванні, приведеному Ньютоном, він був встановлений ще Галілеєм: будь-яка матеріальна точка (тіло) зберігає стан спокою або рівномірного прямолінійного руху доти, доки дія з боку інших тіл не примусить її змінити цей стан. Іншими словами, за відсутності зовнішніх впливів (а, вірніше, при їхній компенсації) тіло покоїться або рухається прямолінійно без зміни швидкості (по інерції). У іншому формулюванні, цей закон звучить так: існують такі системи відліку, щодо яких поступально рухомі тіла зберігають свою швидкість сталою, якщо на них не діють інші тіла (або їхня дія компенсується). Визначення: системи відліку, щодо яких матеріальна точка, вільна від зовнішніх дій, або покоїться, або рухається рівномірно і прямолінійно, називаються інерціальними системами відліку. Твердження про існування інерціальних систем відліку складає зміст першого закону Ньютона – він виконується тільки в таких системах відліку.

Системи відліку, рухомі відносно інерціальної системи відліку із прискореннями, називаються неінерціальними. Дослідним шляхом встановлено, що інерціальною можна вважати геліоцентричну (зоряну) систему відліку, початок координат якої знаходиться в центрі Сонця, а осі проведені у напрямках на певні зірки. Система відліку, зв'язана із Землею, точно кажучи, неінерціальна, оскільки Земля обертається навколо власної осі і навколо Сонця. Проте при вирішенні багатьох задач ефекти, пов'язані із її неінерціальністю, нехтовно малі, і в цих випадках її можна вважати інерціальною.

Щоб передбачити характер руху тіла у кожному конкретному випадку, необхідно знати характер діючих на нього сил. У механіці вивчаються сили тяжіння (гравітаційні), сили пружності і сили тертя.

1. Сили тяжіння – це сили притягання, які підпорядковуються закону Всесвітнього тяжіння, відкритого Ньютоном при вивченні руху небесних тіл на основі законів Кеплера і основних законів динаміки: між двома матеріальними точками із масами m ₁ та m ₂ діє сила взаємного притягання, пропорційна добутку їхніх мас і обернено пропорційна квадрату відстані між ними:

(2.6)

де G= 6,67×10^-11 н×м²/кг²– гравітаційна стала. Дві планети, відстань між якими значно більша їхніх лінійних розмірів, можна розглядати, як матеріальні точки при визначенні гравітаційної взаємодії між ними. Якщо ж тіла не можна вважати матеріальними точками, то їх можна уявляти, як сукупність матеріальних точок, а результуючу силу притягання між тілами знаходять геометричним підсумовуванням взаємодій між їхніми окремими точками. Маси, що входять у вираз закону всесвітнього тяжіння, називаються гравітаційними. На відміну від інертних мас, які служать коефіцієнтом пропорційності між діючою на тіло силою, і його прискоренням, гравітаційні маси визначають силу гравітаційної взаємодії між тілами. Взаємне тяжіння властиве всім без виключення матеріальним тілам, існує у будь-якому середовищі і здійснюється за допомогою гравітаційного поля. Разом із речовиною, поле тяжіння, разом з іншими фізичними полями, є однією із форм матерії.

Сила тяжіння – це сила, із якою всі тіла притягуються до Землі і спрямована вертикально вниз. Під дією сили тяжіння до Землі, згідно узагальненому закону Галілея, всі тіла в даному місці земної кулі падають із однаковим прискоренням g (позначення від англійського слова «gravitation» – «тяжіння»), яке називається прискоренням вільного падіння або напруженістю гравітаційного поля Землі. Його значення змінюється поблизу поверхні Землі із широтою в межах від 9,78 м/с² на екваторі до 9,83 м/с² на полюсах. Це обумовлено добовим обертанням Землі навколо своєї осі, з одного боку, та сплюснутістю Землі – з іншого. (При вирішенні практичних задач вважають g= 9,80 м/с²). На підставі другого закону Ньютона, сила тяжіння визначається співвідношенням: P= m ×g. Якщо добовим обертанням Землі навколо своєї осі знехтувати, для тіла масою m поблизу її поверхні можна записати формулу зв'язку між силою тяжіння та силою притягання:

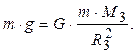Звідки, (2.7)

де М ₃ – маса Землі, R ₃ – радіус Землі.

Вагою тіла називається сила, із якою тіло внаслідок притягання до Землі тисне на опору або розтягує нитку підвісу, утримуючі тіло від вільного падіння. Сила тяжіння діє завжди, а вага проявляється тільки у тому випадку, коли на тіло окрім сили тяжіння діють ще і інші сили, внаслідок чого тіло рухається не із прискоренням вільного падіння g, а з меншим прискоренням а. Якщо тіло у полі тяжіння Землі рухається із прискоренням а¹g, то до нього окрім сили тяжіння прикладена додаткова сила N, звана силою реакції опори або силою натягу нитки підвісу. Рівняння руху тіла (другий закон Ньютона) у цьому випадку має вигляд:

(2.8)

Тоді вага тіла (згідно із третім законом Ньютона):

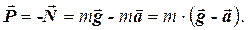(2.9)

Це означає, що якщо тіло покоїться або рухається рівномірно (V=const), то вага тіла дорівнює силі тяжіння. При русі тіла із прискоренням, залежно від напрямку руху, вага тіла може бути як більшою, так і меншою за силу тяжіння. Якщо тіло вільно рухається у полі тяжіння у будь-якому напрямку і по будь-якій траєкторії, то а=g, а вага тіла буде дорівнювати нулю, тобто тіло буде невагомим. Стан тіла, при якому воно рухається тільки під дією сили тяжіння (вільно падає), називається станом невагомості. Наприклад, невагомими є тіла у кабіні космічного корабля, вільно рухомого у космосі.

2. Сили пружності виникають в результаті взаємодії тіл, яка супроводжується їхньою деформацією. Деформацією називають зміну форми і розмірів тіла під дією прикладених сил. Деформація називається пружною, якщо після припинення дії зовнішніх сил, вона повністю зникає (тобто тіло повністю відновлює свою форму). Деформація, яка залишається в тілі після припинення дії зовнішніх сил, називається залишковою або пластичною. Потрібно відзначити, що деформації реальних тіл є завжди пластичними, оскільки після припинення зовнішньої дії вони ніколи повністю не зникають. Проте, при малих навантаженнях, коли залишкові деформації малі, ними можна нехтувати. Для пружних деформацій справедливий закон Гука: сила пружності, яка виникає у пружно деформованому тілі, прямо пропорційна величині його абсолютної деформації:

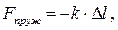(2.10)

де D l – абсолютна деформація тіла (якщо до кінців стрижня завдовжки l ₀ прикласти дві протилежні сили, то його довжина змінюється на D l. При розтягуванні - D l позитивне, а при стисненні – негативне); k – коефіцієнт пропорційності (при розгляді сили пружності пружини коефіцієнт k називають жорсткістю пружини).

Закон Гука може бути сформульований і у більш загальному вигляді: для малих (пружних) деформацій механічна напруга, яка виникає у деформованому тілі, прямо пропорціональна його відносній деформації:

(2.11)

де s=F/S – сила, діюча на одиницю поперечного перерізу тіла, називається механічною напругою, а e= D l/l ₀ – відносна деформація тіла – відношення абсолютної деформації до початкової довжини. Коефіцієнт пропорційності між ними Е характеризує пружні властивості матеріалу тіла і називається модулем Юнга. Можна легко показати, що обидва ці вирази еквівалентні.

3. Сили тертя виникають при стиканні поверхонь тіл і перешкоджають їхньому взаємному переміщенню. Вони спрямовані по дотичній до поверхонь (або шарам рідини, газу), які труться, і протидіють відносному зсуву цих поверхонь (завжди спрямовані протилежно відносній швидкості переміщення). Сили тертя залежать від відносних швидкостей руху тіл. Вони можуть бути різної природи, але в результаті їхньої дії механічна енергія стичних тіл завжди перетворюється на внутрішню енергію (про енергію поговоримо на наступній лекції).

Розрізняють декілька видів сил тертя.

а) Тертя спокою – виникає за відсутності відносного переміщення стичних тіл. Максимальна сила тертя спокою визначається співвідношенням:

(2.12)

де m ₀ – коефіцієнт тертя спокою, залежний від властивостей (природа та стану) стичних поверхонь, N – сила нормального тиску, що притискує одну до одної поверхні, які труться. Відносний рух тіл виникне, коли зовнішня дотична сила дії на тіло перевищить силу тертя спокою.

б) Зовнішнє (сухе) тертя – виникає у площині дотику двох стичних тіл при їхньому відносному переміщенні. Розрізняють види сухого тертя: тертя ковзання, яке виникає при ковзанні тіла по поверхні опори; тертя котіння – виникає, якщо тіло котиться по поверхні опори. Сила тертя ковзання визначається згідно із законом:

(2.13)

де m - коефіцієнт тертя ковзання. Сила тертя котіння визначається згідно із законом, встановленим Кулоном:

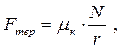(2.14)

де r – радіус тіла, яке котиться, m_к – коефіцієнт тертя котіння.

в) Внутрішнє (в'язке) тертя – тертя між частинами одного і того ж тіла, наприклад, між різними шарами рідини або газу, швидкості яких з мінюються від шару до шару. На відміну від зовнішнього тертя, в даному випадку тертя спокою відсутнє. При переміщенні одних шарів реальної рідини або газу щодо інших, виникають сили внутрішнього тертя, спрямовані по дотичній до поверхні шарів. Дія цих сил проявляється у тому, що з боку більш швидких рухомих шарів на шари, рухомі повільніше, діє прискорююча сила. У свою чергу, з боку більш повільних рухомих шарів на шари, рухомі швидше, діє сила гальмуюча. Характер залежності в'язкого тертя від температури різний для рідин і газів: для рідин при збільшенні температури в'язкість зменшується, а для газів – збільшується. Це говорить про відмінність в них механізмів внутрішнього тертя.

Одним із методів дослідження в'язкості рідин служить метод Стокса, заснований на вимірюванні швидкостей руху невеликих тіл сферичної форми. Встановлена дослідним шляхом, сила опору рівномірному руху кульки в рідині (сила Стокса) визначається співвідношенням:

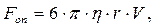(2.15)

де h - коефіцієнт динамічної в'язкості, r – радіус кульки, V - швидкість її рівномірного руху.

Розглядаючи динаміку поступального руху, ми ввели поняття сили і маси. При вивченні динаміки обертального руху потрібне застосування нових його динамічних характеристик – моменту сили і моменту інерції. Моментом сили нази-

	вається векторна фізична величина, визначувана векторним добутком радіусу-вектора r точки прикладання сили на вектор цієї сили F: (2.16) Напрям вектора моменту сили визначають правилом векторного добутку (правилом правого гвинта). Модуль век-тора моменту сили: M=F×r× sin a = F×l, де a - кут між векторами r і F, r× sin a = l – найкоротша відстань між лінією
Рис.2.1.

дії сили і початком відліку системи координат, звана плечем сили (рис.2.1). Одиниця виміру моменту сили – Ньютон-метр (Н×м).

Мірою інертності тіла при поступальному русі є його маса. Інертність тіла при обертальному русі залежить не тільки від самої маси, але і від її розподілу відносно осі обертання. Мірою інертності при обертальному русі служить момент інерції тіла відносно осі обертання. Моментом інерції матеріальної точки щодо

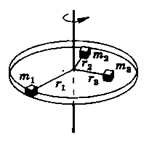Рис.2.2.

осі обертання називають скалярну фізичну величину, рівну добутку маси цієї точки на квадрат відстані від осі: Ii= =mi×ri ^2. Одиниця виміру моменту інерції – кілограм-метр в квадраті (кг×м^2). Це адитивна величина: момент інерції тіла дорівнює сумі моментів інерції його частин (рис.2.2). Момент інерції тіла щодо осі обертання дорівнює сумі моментів інерції матеріальних точок, із яких складається це тіло:

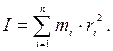(2.17)

У загальному випадку, якщо тіло суцільне і є сукупністю точок із малими масами dm, його момент інерції визначається інтегруванням:

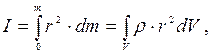(2.18)

де r=m/V – густина однорідного тіла. Момент інерції тіла залежить від того, щодо якої осі воно обертається і як розподілена маса тіла за об'ємом. Найпростіше визначаються моменти інерції тіл, які мають правильну геометричну форму і рівномірний розподіл маси за об'ємом. Нижче приведені моменти інерції деяких тіл щодо осей, які проходять через центри інерції.

Форма тіла	Момент інерції	Форма тіла	Момент інерції
Порожнистий циліндр (обруч) радіусу R	I0=m×R^2.	Суцільний циліндр (диск) радіусу R	I0=0,5m×R^2.
Тонкий одноріднийстрижень довжиною l	I 0 =m×l ^2 / 12.	Одноріднакуля радіусу R	I0=0,4m×R^2.

Якщо потрібно визначити момент інерції тіла щодо довільної осі, слід скористатись теоремою Штейнера: момент інерції тіла I щодо довільної осі обертання дорівнює сумі моменту інерції I ₀ щодо осі, паралельній даній, яка проходить через центр інерції тіла, та добутку маси тіла m на квадрат відстані між цими осями d:

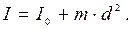(2.19)

Основний закон динаміки обертального руху, як і другий закон Ньютона для поступального руху, встановлює зв'язок між динамічними характеристиками обертального руху: кутове прискорення точки e при її обертанні навколо нерухомої осі пропорційне сумарному обертаючому моменту сил М, прикладених до тіла, і обернено пропорційне до моменту інерції І цього тіла:

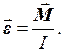(2.20)

Як і для поступального руху, основний закон динаміки обертального руху може бути записаний у іншому вигляді. Для того, щоб його записати, введемо ще одну динамічну характеристику. Моментом імпульсу матеріальної точки щодо нерухомої точки О називають векторну фізичну величину, визначувану векторним добутком радіусу-вектора r_i цієї матеріальної точки, проведеного із точки О, на вектор імпульсу p_i= m_i× V_i цієї матеріальної точки:

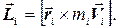(2.21)

Напрямок вектора моменту імпульсу визначається правилом векторного додатку

(правого гвинта). Модуль вектора моменту імпульсу: Li= =ri×pi× sin a = pi×l, де a - кут між векторами ri та pi, l=ri× sin a – найкоротша відстань між точкою О та напрямком імпульсу частинки, звана плечем імпульсу (рис.2.3). При обертанні твердого тіла кожна його точка рухається зі своєю лінійною швидкістю Vi=ri×w, де ri – радіус кола, яке описує частинка твердого тіла масою mi навколо нерухомої осі Z, w - кутова швидкість обертання, однакова для всіх точок тіла. Швидкість Vi та імпульс частинки рi=mi×Vi пер-

Рис.2.3.

пендикулярні цьому радіусу, тобто радіус є плечем вектора імпульсу. Моментом імпульсу окремої частинки щодо нерухомої осі Z називається величина L_iz=r_i×p_i= =r_i×m_i×V_i, спрямована вздовж осі Z згідно правилу правого гвинта. Момент імпульсу твердого тіла щодо нерухомої осі обертання Z дорівнює сумі моментів імпульсів окремих його частинок щодо тієї ж осі:

(2.22)

де I_z – момент інерції тіла щодо осі Z. Одиниця виміру моменту імпульсу – кілограм-метр в квадраті за секунду (кг×м²/с). Момент імпульсу твердого тіла – вектор, співпадаючий за напрямком із вектором кутової швидкості. Використовуючи поняття моменту імпульсу, перепишемо основний закон динаміки обертального руху:

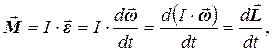(2.23)

тобто, швидкість зміни моменту імпульсу твердого тіла щодо деякої осі обертання дорівнює геометричній сумі моментів всіх зовнішніх сил і відбувається у напрямку дії результуючого моменту сил.

Лекція № 3

Дата добавления: 2014-11-07