Закони збереження. Енергія. Робота

У класичній механіці, окрім застосування законів Ньютона, є ще одна модель спрощення задач про рух тіл. Механічною системою називають сукупність матеріальних точок або тіл, які розглядаються як єдине ціле. Утворюючи механічну систему, тіла можуть взаємодіяти як між собою, так і з тілами, які не належать даній системі. Тому сили, діючі на тіла системи, діляться на внутрішні і зовнішні. Сили взаємодії між матеріальними точками (або тілами) механічної системи називають внутрішніми. А сили, із якими на матеріальні точки механічної системи діють зовнішні тіла, називаються зовнішніми. У ряді випадків можна припустити, що задача переміщення об'єктів системи розглядається ізольовано від інших тіл, які не входять в дану систему. Така механічна система, на яку не діють зовнішні сили, називається замкнутою. Реально, звичайно, цього немає. Це модель, але завжди можна припустити, що внутрішні взаємодії тіл системи набагато більші, ніж зовнішні.

Для замкнутих систем існують такі функції координат і швидкостей утворюючих систему частинок, які зберігають в процесі руху постійне значення. Ці функції носять назву інтегралів руху. Адитивних інтегралів руху (таких, що інтеграл руху механічної системи, яка складається із частин, взаємодією між якими можна знехтувати, дорівнює сумі інтегралів руху цих частин) всього три: це імпульс, момент імпульсу і енергія. Таким чином, для замкнутих систем можна ввести закони збереження параметрів стану і руху тіл, загальніші, ніж закони Ньютона. У класичній механіці таких законів три: закони збереження імпульсу, моменту імпульсу і енергії (про енергію поговоримо декілька пізніше).

У основі сучасної механістичної моделі Всесвіту лежать закони збереження імпульсу і моменту імпульсу, які відбивають такі властивості симетрії простору, як його однорідність та ізотропність. Однорідність простору полягає у рівноправності всіх його точок: при паралельному переносі замкнутої системи у просторі як цілого, її фізичні властивості і закони руху не змінюються, іншими словами, не залежать від вибору положення початку координат інерціальної системи відліку. Під ізотропністю простору розуміють рівноправність всіх напрямків у просторі. Іншими словами, це інваріантність (незалежність) фізичних законів щодо вибору напрямків осей координат системи відліку (щодо повороту замкнутої системи у просторі на будь-який кут).

Якщо частинка масою m_i має швидкість V_i, а її радіус-вектор у деякій системі відліку r_i, то імпульсом (кількістю руху) частинки називається векторна величина p_i= m _i × V_i, а моментом імпульсу - векторна величина L_i= [ r_i ´ p_i ]. Розглядаючи механічну систему із n- тіл, маси та швидкості яких відповідно дорівнюють m ₁, m ₂,…., m_n та V ₁, V ₂,…., V_n. Другий закон Ньютона для кожного із тіл системи може бути записаний так:

(3.1)

де F ₁¢, F ₂¢,….., F_n¢ – рівнодіючі внутрішніх сил, діючих на кожне тіло системи, F ₁, F ₂,….., F_n - рівнодіючі зовнішніх сил відповідно. Після почленного додавання рівнянь, одержимо:

(3.2)

При додаванні враховано, що - сумарний імпульс системи, а геометрична сума всіх внутрішніх сил механічної системи за третім законом Ньютона дорівнює нулю. У разі замкнутої системи зовнішні сили відсутні (їхня геометрична сума дорівнює нулю), тому:

(3.3)

Отже,

(3.4)

Ця рівність висловлює закон збереження імпульсу: повний імпульс замкнутої системи тіл зберігається, тобто не змінюється зі спливанням часу. Це означає, що якщо у одного із тіл замкнутої системи змінився імпульс, то це могло відбутись тільки за рахунок зміни імпульсів інших тіл цієї системи.

Як було показано на попередній лекції, основний закон динаміки для обертального руху свідчить, що швидкість зміни моменту імпульсу твердого тіла (системи матеріальних точок) дорівнює результуючому моменту (алгебраїчній сумі) всіх зовнішніх сил:

(3.5)

Для замкнутої системи сумарний момент всіх зовнішніх сил, які діють на систему щодо довільної нерухомої осі, дорівнює нулю, тобто М= 0, тому і d L /dt= 0, звідки L= const. Ця рівність висловлює закон збереження моменту імпульсу: сумарний момент імпульсу замкнутої системи матеріальних точок зберігається, тобто не змінюється зі спливанням часу. Нагадаємо, що момент імпульсу твердого тіла щодо нерухомої осі L= I× w, де I – момент інерції тіла щодо цієї осі обертання, w - кутова швидкість його обертання. Закон збереження моменту імпульсу може бути записаний так: I ₁ × w ₁₌ I ₂ × w ₂. Це означає, що якщо у обертового тіла внаслідок будь-яких причин відбудеться збільшення моменту інерції, то це приведе до зменшення його кутової швидкості обертання (приклади – обертання фігуриста або акробата).

Таким чином, закони збереження імпульсу і моменту імпульсу обумовлені симетрією простору і виконуються при будь-яких взаємодіях - про що свідчать численні дані експериментів. Зазначимо, що тривимірність простору визначає векторну природу цих фізичних параметрів p та L. Із приведених міркувань виходить, що зміна цих параметріввизначається тільки зовнішніми силами: зміна положення замкнутої системи у просторі сама по собі не може змінити її стану; така зміна можлива тільки в результаті взаємодії з іншими системами. Отже, ці закони справедливі у мега-, макро- і мікросвіті, тому вони називаються великими законами збереження.

Ще одним інтегралом руху є енергія. Поняття енергії не є простим. У загальному значенні, під енергією розуміють скалярну фізичну величину, яка є універсальною мірою різних форм руху та взаємодії матерії. Вона відбиває кількісну зміну стану тіла, його рухи або зміну його структури при відповідних взаємодіях. Іншими словами, енергія – це просто число, яке розраховується за певними правилами. Як показав А.Ейнштейн, повна енергія системи масою m, визначається співвідношенням: Е=m×с ², де с – швидкість поширення світла у вакуумі. Для нас важливо, що поняття енергії тісно пов'язане із поняттям механічної роботи. Обидва ці поняття, разом із уявленнями про довжину, час і масу, історично склалися на інтуїтивному рівні досить давно. І тому зрозумілі навіть при гуманітарному сприйнятті світу: щоб виконати роботу, треба витратити енергію.

Природа нашого Всесвіту така, що у замкнутій ізольованій системі різні форми енергії можуть перетворюватись одна на одну без втрат: іншими словами, при будь-якому фізичному процесі сумарна енергія не змінюється. Це означає, що вона зберігається у часі, тобто є третім інтегралом руху (після імпульсу і моменту імпульсу, про які ми говорили раніше). Закон збереження енергії був сформульований у 1847 році німецьким фізиком Геймгольцем. Він обумовлений просторово-часовою симетрією і відбиває однорідність часу (це означає, що час скрізь спливає однаково, і фізичні закони інваріантні щодо вибору початку відліку часу). Зазначимо, що спливання часу саме по собі не може спричинити зміну фізичного стану системи. Природа ніби дозволяє змінювати види енергії, але не передбачає її народження або знищення. Для енергії суттєвим є те, що абсолютні її значення довільні. Оскільки рух у різних системах відліку є відносним, а ми ведемо мову про зміну параметрів руху, то це означає, що ми розглядаємо лише зміни енергії, тобто вона відносна.

Відповідно до різних форм руху матерії говорять про різні види енергії – механічну, внутрішню, ядерну та інші. В процесі взаємодії тіл, форми руху матерії можуть змінюватись. Зміна виду енергії обумовлена дією на тіло сил і пов'язана зі здійсненням роботи. Робота сили – це кількісна характеристика процесу обміну енергією поміж взаємодіючими тілами. Робота, здійснена сталою силою F при переміщенні тіла на прямолінійній ділянці шляху S, визначається співвідношенням (рис.3.1):

	(3.6) де Fs – проекція сили на напрямок переміщення тіла, a - кут між векторами сили та переміщення. Робота – скалярна величина. Якщо кут a гострий, то cos a> 0, і роботу вважають додатною. Якщо a тупий, то cos a< 0, і робота від¢ємна. Якщо a=p/ 2, то cos a= 0 і А= 0, тобто сила, яка діє перпендикулярно переміщенню тіла, ро-
Рис.3.1.

боти не здійснює. Одиниця виміру роботи – Джоуль (Дж): 1 Дж=1 Н×м=1 кг×м²/с². У загальному випадку на тіло може діяти зовнішня змінна сила, яка змінюється як за величиною, так і за напрямом. Під дією змінної сили тіло переміщується по де-

	якій траєкторії. Розглянемо елементарне переміщення dS, на якому діючу силу F вважаємо сталою. Елементарна робота, здійснювана силою на цьому переміщенні, визначається скалярним добутком: (3.7) Для обчислення роботи сили на заданій ділянці траєкторії руху 1-2, потрібно знати залежність F (S) та проінтегрувати
Рис.3.2.

її по всій ділянці шляху:

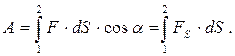(3.8)

Графічно шукана робота визначається площею фігури під кривою, яка відображає залежність F (S), при цьому робота позитивна, якщо площа фігури береться над віссю S. Фізична величина, яка характеризує швидкість виконання роботи (роботу, здійснену силою за одиницю часу), називається потужністю:

(3.9)

Потужність можна виразити через силу, яка здійснює роботу. Якщо за час dt сила F здійснює роботу dA = F × d r, то миттєва потужність, яка розвивається нею в даний момент часу, становить:

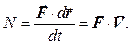(3.10)

Одиниця виміру потужності – Ватт (Вт): 1 Вт=1 Дж/с=1 кг×м²/с³.

Здатність тіл здійснювати механічну роботу характеризується запасом їхньої енергії. У механіці розрізняють два види енергії: кінетичну і потенціальну. Кінетична енергія - це енергія механічного руху тіла (або механічної системи тіл). Вона визначається роботою, яку може здійснити тіло внаслідок того, що воно володіє певною швидкістю. Нехай тіло масою m рухається прямолінійно зі швидкістю V і знаходиться під дією сили F, яка гальмує його рух. Згідно із другим законом Ньютона:

(3.11)

Елементарна робота, здійснювана рухомим тілом проти сили F на шляху d S, дорівнює:

(3.12)

Якщо швидкість тіла зменшується при цьому від V ₁до V ₂, то сумарна робота становить:

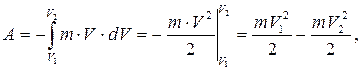(3.13)

тобто робота дорівнює зменшенню кінетичної енергії тіла, оскільки вона здійснюється проти зовнішніх сил. Якщо зовнішні сили діють на тіло і здійснюють роботу, то кінетична енергія тіла зростає. Отже, кінетична енергія тіла, рухомого зі швидкістю V, дорівнює:

(3.14)

Теорема про кінетичну енергію: приріст кінетичної енергії матеріальної точки на деякому переміщенні дорівнює алгебраїчній сумі робіт всіх сил, які діють на матеріальну точку на цьому ж переміщенні:

(3.15)

Характерні властивості кінетичної енергії: вона завжди додатна, неоднакова в різних системах відліку і є функцією стану системи. Одиниця виміру енергії – Джоуль (Дж): 1 Дж=1 Н×м=1 кг×м²/с².

Визначимо кінетичну енергію твердого тіла, яке обертається навколо нерухомої осі. Розіб'ємо це тіло на n матеріальних точок. Кожна із них рухається із лінійною швидкістю V_i=w×r_i, тому кінетична енергія і-тої точки становить:

(3.16)

Повна кінетична енергія твердого тіла, яке обертається, дорівнює сумі кінетичних енергій всіх його матеріальних точок:

(3.17)

де I - момент інерції тіла щодо осі обертання. Якщо тіло здійснює одночасно поступальний і обертальний рух (котиться), то його повна кінетична енергія складається із двох частин: кінетичних енергій поступального та обертального рухів, тобто:

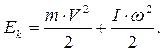(3.18)

При обертанні твердого тіла, згідно із теоремою про кінетичну енергію, елементарна робота зовнішніх сил дорівнює приросту його кінетичної енергії:

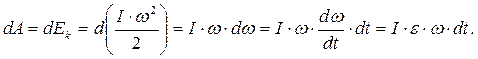(3.19)

Враховуючи, що I×e=M (основний закон динаміки обертального руху), а також w×dt=dj, ми отримаємо:

(3.20)

Робота зовнішніх сил при повороті твердого тіла на деякий кут j дорівнює:

(3.21)

Тобто, при обертанні твердого тіла навколо нерухомої осі, робота зовнішніх сил визначається дією моменту цих сил відносно даної осі. Якщо момент сил щодо осі дорівнює нулю, то ці сили роботи не здійснюють.

Якщо тіло або частинка у кожній точці простору зазнають дії інших тіл, то кажуть, що вони знаходяться у силовому полі. Приклади: поле тяжіння, електростатичне поле і інші. Якщо ці сили однакові за величиною і напрямом у кожній точці, поле називають однорідним. Якщо сили залежать тільки від відстані між взаємодіючими частинками та спрямовані по прямій, яка з¢єднує центри мас цих частинок, то такі сили називають центральними. Якщо поле змінюється у часі, воно називається нестаціонарним, а якщо не змінюється – стаціонарним. Поля, в яких робота сили не залежить від форми шляху, по якому рухалась частинка, а залежить лише від положення початкової і кінцевої точок траєкторії, називають потенціальними, а сили, які в ньому діють, - консервативними. У потенціальному полі робота сил вздовж будь-якого замкнутого контуру дорівнює нулю, що є необхідною і достатньою умовою незалежності роботи від форми шляху та ознакою будь-якого потенціального поля. Прикладом неконсервативних сил – залежних від форми шляху - є сили опору та тертя.

Потенціальною енергією називають частину механічної енергії системи, залежну від взаємного розташування частинок системи, їхнього положення у зовнішньому силовому полі та характеру сил взаємодії між ними. При переміщенні частинки у потенціальному полі, робота консервативних сил поля на фіксованій ділянці шляху дорівнює зменшенню потенціальної енергії частинки у цьому полі:

(3.22)

У класичній механіці взаємодія частинки із навколишніми тілами описується або за допомогою сил, або за допомогою потенціальної енергії. При елементарній (нескінченно малій) зміні конфігурації системи, робота консервативних сил дорівнює приросту потенціальної енергії, узятому зі зворотним знаком:

Звідки, (3.23)

Це означає, що потенціальна енергія – це функція, визначувана із точністю до деякої довільної сталої. Проте, це не відображається на фізичних законах, оскільки в них входить або різниця потенціальних енергій у двох положеннях тіла (конфігураціях системи), або похідна потенціальної енергії по координатах. Тому потенціальну енергію тіла у деякому певному положенні вважають рівною нулю (вибирають нульовий рівень відліку), а енергію тіла у інших положеннях відлічують відносно цього нульового рівня. Конкретний вид функції U (r) залежить від характеру силового поля.

Як приклад можна привести енергію піднятого над землею тіла та енергію стиснутої пружини. І підняте тіло, і стиснута пружина можуть здійснювати роботу. При падінні тіла масою m, піднятого на висоту h, сила тяжіння здійснює роботу А, величина якої залежить від початкового і кінцевого положень тіла (тобто, від висоти h), і дорівнює mg×h. Отже, підняте тіло володіє потенціальною енергією, рівною тій роботі, яку здійснює сила тяжіння, коли тіло досягає кінцевого положення: U=mgh.

Перемістимо тіло, на яке діє пружна сила F=-k×x із точки з координатою x ₁ у точку з координатою x ₂. Елементарна робота цієї сили на елементарному переміщенні dx становить: dA=-k×x×dx. Тому робота цієї сили на всьому шляху визначається інтегруванням:

(3.24)

Очевидно, що пружна пружина, розтягнута на довжину x, має потенціальну енергію U=k×x ² / 2.

Отже, із виведеної вище формули виходить, що для консервативних сил зв'язок між потенціальною енергією та силою поля має вигляд:

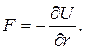(3.25)

Символ частинної похідної ¶/¶ r свідчить про те, що похідна береться по певному напрямку. У загальному випадку потенціальна енергія є функцією координат, тобто U=U (x, y, z). Тому, у декартовій системі координат визначають проекції вектора F на осі X, Y, Z, тоді:

(3.26)

де

(3.27)

проекції сили на відповідні координатні осі, - одиничні вектори координатних осей. Величина, яка стоїть у дужках, називається градієнтом скалярної функції. Попередній вираз (3.26) можна переписати у вигляді:

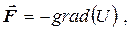(3.28)

тобто, сила F поля дорівнює градієнту потенціальної енергії зі зворотним знаком.

Таким чином, якщо розглядати замкнену систему матеріальних точок, між якими діють тільки консервативні сили, то ці сили взаємодії здійснюють механічну роботу. З одного боку, згідно із теоремою про кінетичну енергію, ця робота іде на збільшення кінетичної енергії системи, а з іншого боку, ця ж робота дорівнює спаду потенціальної енергії системи. Тому, для двох довільних станів системи можна записати:

(3.29)

Звідки випливає:

(3.30)

Сума кінетичної та потенціальної енергії системи називається повною механічною енергією системи, а одержана вище рівність є законом збереження механічної енергії, який формулюється так: у системі тіл, між якими діють тільки консервативні сили, повна механічна енергія системи зберігається, тобто не змінюється зі спливанням часу.

Цей закон є наслідком однорідності часу, яка полягає у тому, що фізичні закони інваріантні щодо вибору початку відліку часу. Наприклад, при вільному падінні тіла у полі сил тяжіння, його швидкість і пройдений шлях залежать лише від початкової швидкості та тривалості вільного падіння тіла, і не залежать від того, в який саме момент часу воно стало падати.

За наявності в системі неконсервативних сил (сил тертя або опору руху), механічна енергія системи поступово зменшується (розсіюється) за рахунок перетворення в інші немеханічні форми - у тепло. Такий процес називається дисипацією (розсіюванням) енергії. Сили, які приводять до неї, називаються дисипативними. Такі сили завжди спрямовані протилежно швидкостям руху частинок і спричиняють їхнє гальмування. Строго кажучи, всі системи в природі є дисипативними, оскільки сили тертя і опору руху присутні завжди. Отже, у цих випадках закон збереження механічної енергії несправедливий. Проте, при «зникненні» механічної енергії, завжди з'являється еквівалентна кількість енергії іншого вигляду: енергія ніколи не зникає і не з'являється знов, вона лише перетворюється із одного виду з іншій. У цьому полягає фізична сутність закону збереження та перетворення енергії – сутність незнищуваності матерії і її руху. Цей закон – фундаментальний закон природи, який справедливий як для систем макроскопічних тіл, так і для систем мікрочастинок.

Основними характеристиками будь-якого потенціального поля у кожній його точці є напруженість Е і потенціал j. Напруженість – силова характеристика поля, це векторна величина. Наприклад, під напруженістю гравітаційного поля розуміють силу, яка діє в даній точці поля на тіло одиничної маси:

(3.31)

Вектори напруженості і сили співпадають за напрямком. У гравітаційному полі на тіло діє сила тяжіння, пропорційна його масі m:

(3.32)

Звідки,

(3.33)

Це означає, що величина g, яку на минулій лекції ми назвали прискоренням вільного падіння тіла в даній точці поля, має сенс напруженості гравітаційного поля. Підставивши в цей вираз для сили гравітаційної взаємодії тіла масою m із Землею, маса якої М₃ і радіус R₃ (із закону всесвітнього тяжіння), одержуємо:

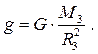(3.34)

Із формули виходить, що прискорення вільного падіння не залежить від маси і розмірів тіла. Гравітаційне поле Землі є центральним – таким, що у всіх його точках вектори напруженості спрямовані уздовж прямих, які перетинаються у одній точці – центрі Землі. На малюнках силові поля зображаються за допомогою силових ліній – ліній, дотичні до яких у кожній точці співпадають із напрямком вектора напруженості. Силовим лініям надаються напрями, співпадаючі із напрямком вектора напруженості (наприклад, силові лінії гравітаційного поля Землі направлені вертикально вниз).

Потенціалом поля називають його енергетичну характеристику, це скалярна величина. Наприклад, потенціал гравітаційного поля визначається потенціальною енергією тіла одиничної маси в даній точці поля:

(3.35)

Одиниця виміру потенціалу гравітаційного поля - Джоуль/кілограм (1 Дж/кг). Обчислимо роботу, здійснювану силами поля тяжіння при віддаленні тіла масою m від Землі. При переміщенні цього тіла у полі тяжіння на відстань dR здійснюється елементарна робота:

(3.36)

Знак “-“ у формулі з'являється тому, що сила тяжіння та переміщення тіла протилежні за напрямком. При переміщенні його із відстані R ₁до R ₂ здійснюється робота:

(3.37)

Витрачена робота у гравітаційному полі не залежить від траєкторії переміщення, а визначається лише початковим та кінцевим положеннями тіла, тобто сили тяжіння консервативні, а поле тяжіння є потенціальним. Для такого поля A=- D U=- (U ₂ -U ₁) = (U ₁ -U ₂). Порівнявши ці формули, одержуємо вираз для потенціальної енергії тіла масою m у будь-якій точці поля тяжіння:

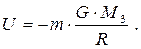(3.38)

Звідки, потенціал поля тяжіння в даній точці:

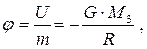(3.39)

де R – відстань від центру Землі до даної точки поля. Якщо R ₂®¥, то U ₂®0, і вираз для роботи набуває вигляду: A=U ₁, а вираз для потенціалу поля тяжіння в даній точці:

(3.40)

Це дозволяє визначити потенціал поля тяжіння в даній точці, як роботу по переміщенню одиничної маси із даної точки поля у нескінченність. Геометричне місце точок із однаковим потенціалом називають еквіпотенціальною поверхнею. Із формули для потенціалу поля тяжіння очевидно, що такими поверхнями є сфери (R= const).

Між напруженістю Е та потенціалом поля j існує зв'язок. З одного боку, робота сили тяжіння dA=F×dr=mg×dr, а з іншого боку, dA=-dU=-m×dj. Прирівнявши ці вирази, одержуємо:

(3.41)

Звідки,

(3.42)

Величина dj/dr характеризує зміну потенціалу на одиницю довжини у напрямку переміщення і називається градієнтом потенціалу. Знак мінус свідчить про те, що вектор напруженості g (у загальному випадку, напруженість позначається E) спрямований у бік спадання потенціалу.

Лекція № 4

Дата добавления: 2014-11-07