
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение смеси нефти, воды и газа в пористой среде
|
|
|
|
Экспериментально изучался поток при одновременном содержании в пористой среде нефти, воды и газа. Опытами установлено, что в зависимости от объемного насыщения порового пространства различными компонентами возможно одно-, двух-и трехфазное движение. Результаты опытов обычно изображают в виде треугольных диаграмм (рис. 1.8). Вершины треугольника соответствуют 100 %-ному насыщению породы одной из фаз; стороны треугольника, противолежащие вершинам,— нулевому насыщению этой фазы.

Рис. 1.8. Области распространения одно-, двух- и трехфазного потоков
Кривые линии, проведенные на основании экспериментальных данных, ограничивают на диаграмме возможные области одно-, двух и трехфазного потока. Так, при газонасыщенности среды менее 10% и нефтенасыщенности менее 20% в потоке практически будет содержаться одна вода.
Область существования трехфазного потока (заштрихованная центральная часть) расположена в пределах насыщенности песка: нефтью —от 23 до 50%, водой —от 33 до 64 %, газом — от 14 до 30%. Эти пределы получены для несцементированных песков; для других пород они могут быть несколько отличными.
При опытах в качестве жидкости и газа использовались керосин вязкостью 1,67 мПа-с (0,25%-ный раствор поваренной соли) и азот, в качестве пористых сред —пески с проницаемостью «от 5,4 до 16,2 мкм2.
7. ЗАВИСИМОСТЬ ПРОНИЦАЕМОСТИ ОТ ПОРИСТОСТИ И РАЗМЕРА ПОР
Прямой зависимости между проницаемостью и пористостью горных пород не существует. Например, трещиноватые известняки, имеющие незначительную пористость, часто обладают большой проницаемостью и, наоборот, глины, иногда характеризующиеся высокой пористостью, практически непроницаемы для жидкостей и газов, так как их поровое пространство слагается каналами субкапиллярного размера. Однако на основании среднестатистических данных можно сказать, что более проницаемые породы часто и более пористые.
Проницаемость пористой среды зависит преимущественно от размера поровых каналов, из которых слагается поровое пространство. Поэтому изучению структуры, строения и размеров пор уделяется большое внимание.
Получим зависимость проницаемости от размера пор с учетом законов Дарси и Пуазейля. Пористую, среду представим в виде системы прямых трубок одинакового сечения с длиной L, равной длине пористой среды. По закону Пуазейля расход Q жидкости через такую пористую среду составит
 (15)
(15)
где n — число пор, приходящихся на единицу площади фильтрации; R —радиус поровых каналов (или средний радиус пор среды); F — площадь фильтрации; Dр —перепад давления; m — динамическая вязкость жидкости; L — длина пористой среды.
Коэффициент пористости среды

Подставляя в формулу (15) вместо npR2 значение пористости m, получим
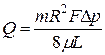 (16)
(16)
По закону Дарси расход жидкости через эту же пористую среду
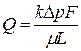 (17)
(17)
Здесь k — проницаемость пористой среды. Приравнивая правые части формул (17) и (16), получим 
откуда  (18)
(18)
или  (19)
(19)
Величина R, определенная по формуле (19), характеризует радиус пор идеальной пористой среды, обладающей пористостью m и проницаемостью k. В приложении к реальной пористой среде величина R имеет условный смысл и не определяет среднего размера пор, так как не учитывает их извилистое и сложное строение.
По предложению Ф. И. Котяхова средний радиус пор реальных пористых сред
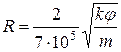 (20)
(20)
где j — структурный коэффициент, характеризующий отличительные особенности строения порового пространства реальных коллекторов. Значение j можно оценить путем измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28 по экспериментальным данным ф изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно определить по эмпирической формуле
 (21)
(21)
Другим широко применяемым методом исследования структуры и строения высокодисперсных пористых тел является экспериментальная порометрия — измерение размеров и характера распределения пор по размерам.
8. РАСПРЕДЕЛЕНИЕ ПОР ПО РАЗМЕРАМ
Наиболее часто относительное содержание в пористой среде пор различного размера определяют методом вдавливания ртути в образец или методом полупроницаемых перегородок.
В первом случае отмытый от нефти сухой образец помещают в камеру, заполняемую ртутью после вакуумирования. Ртуть вдавливается в поры образца специальным прессом при ступенчатом повышении давления. «Радиус» пор, в которые при этом вдавливается ртуть, определяется по формуле
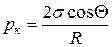 (22)
(22)
где рк — капиллярное давление; s — поверхностное натяжение (для ртути s =480 мН/м); Q - угол смачивания (для ртути можно принять Q =140°); R — радиус пор.
С повышением давления от p 1 до p 2 в камере прибора ртуть вдавливается только в те поры, в которых приложенное давление преодолело капиллярное давление менисков ртути, т. е. ртуть входит в поры, радиус которых изменяется от R 1=2 s cos Q/p 1 до R 2=2 s cos Q/p 2. Суммарный объем этих пор, очевидно, будет равен объему ртути, вдавленной в образец, при повышении давления от p 1 до p 2. Повышая постепенно давление в камере прибора, образец заполняют ртутью до тех пор, пока он не перестанет ее принимать. При этом регистрируют объемы ртути, вдавленной в образец, и соответствующие им давления. Содержание в образце пор различного размера определяют по описанной методике.
При изучении распределения пор по размерам методом полупроницаемых (или малопроницаемых) перегородок обычно пользуются прибором, схема которого изображена на рис. Образец 1, насыщенный жидкостью (водой или керосином), устанавливают в камере 2 на полупроницаемую перегородку (мембрану) 3, также насыщенную жидкостью. В качестве полупроницаемой перегородки используют керамические, фарфоровые или другие плитки, размеры пор которых значительно меньше средних пор образца. Жидкость из керна вытесняется азотом, давление которого создается внутри камеры 2, и регистрируется манометром 4.
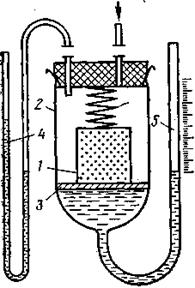
Рис. Прибор для изучения распределения пор по размерам методом полупроницаемых мембран
При повышении давления азот вначале проникает в крупные поры образца и жидкость из них уходит через поры 3 в градуированную ловушку 5. Азот из камеры 2 через перегородку 3 может прорваться только тогда, когда давление в ней превысит капиллярное давление менисков в порах мембраны. Повышая ступенями давление в камере 2 и регистрируя соответствующие объемы жидкости, вытесненные в ловушку при различных давлениях, по формуле (22) определяют состав пор по размерам (измерив предварительно s и Q).
 Результаты анализа обычно изображают в виде дифференциальных кривых распределения пор по размерам (рис.), откладывая по оси абсцисс радиусы поровых каналов в микрометрах, а по оси ординат F(R)=dV/dR — изменения объема пор, приходящиеся на единицу измерения их радиуса.
Результаты анализа обычно изображают в виде дифференциальных кривых распределения пор по размерам (рис.), откладывая по оси абсцисс радиусы поровых каналов в микрометрах, а по оси ординат F(R)=dV/dR — изменения объема пор, приходящиеся на единицу измерения их радиуса.
Дифференциальная кривая распределения пор по их размерам (по Ф. И. Котяхову)
Согласно данным Ф. И. Котяхова, по методу полупроницаемых перегородок получают несколько заниженные результаты. Это, по-видимому, происходит потому, что при расчетах по формуле (22) угол смачивания принимается равным нулю. Если предположить, что при вытеснении керосина воздухом или азотом из образца угол Q = 45°, результаты опытов совпадают в большей степени.
Измерения показывают, что радиусы пор, по которым в основном происходит движение жидкостей, находятся в пределах 5—30 мкм.
Распределение пор по размерам можно также исследовать центробежным методом. Сущность его заключается в том, что при вращении насыщенного жидкостью образца развиваются центробежные силы, способствующие истечению из пор жидкой фазы. При вращении керна в центрифуге с возрастающей скоростью жидкость удаляется из пор меньшего размера. В процессе опыта регистрируют объемы жидкости, вытекающей из образца при соответствующей скорости вращения. По значению скорости рассчитываются центробежная сила и капиллярное давление, удерживающее оставшуюся жидкость в образце. По значению капиллярного давления устанавливается размер пор, из которых вытекла жидкость при данной скорости вращения. Так получают кривую распределения пор по размерам. Большим преимуществом центробежного метода является быстрота операций.
 Легко убедиться, что по данным, полученным в процессе опыта по изучению распределения пор, можно построить кривые капиллярное давление — водонасыщенность пор жидкостью. Типичный ее вид для пород различной проницаемости приведен на рис. По оси абсцисс откладывается водонасыщенность породы (в долях единицы или в процентах), а по оси ординат — капиллярное давление рк, соответствующее данной водонасыщенности SВ.
Легко убедиться, что по данным, полученным в процессе опыта по изучению распределения пор, можно построить кривые капиллярное давление — водонасыщенность пор жидкостью. Типичный ее вид для пород различной проницаемости приведен на рис. По оси абсцисс откладывается водонасыщенность породы (в долях единицы или в процентах), а по оси ординат — капиллярное давление рк, соответствующее данной водонасыщенности SВ.
Рис. Типичные кривые зависимости капиллярное давление — водонасы-щенность пористых сред
Считается, что метод полупроницаемых перегородок позволяет получить зависимости рк—SB, наиболее близкие к пластовым условиям в связи с возможностью использования в опытах воды и нефти в качестве первоначально насыщающей образец фазы и вытесняющей среды. По смачивающим и другим свойствам модельная система приближается к пластовой.
Зависимости рк—SB широко используют при оценке остаточной водонасыщённости пород для изучения строения переходной зоны нефть — вода, вода — газ.
Как следует из рис., характер зависимости рк=f(Sв) в значительной степени определяется проницаемостью пористых сред. Очевидно, другие свойства пород, а также параметры жидкостей влияют на форму кривых рк=f(Sв). Левереттом была впервые сделана попытка учесть влияние свойств пород и жидкостей и свести данные о зависимости капиллярного давления от насыщенности различных пластов в единую зависимость с помощью функции
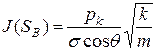 (23).
(23).
Здесь все обозначения прежние.
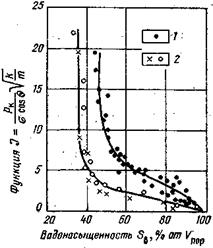 Легко установить по формулам (19) и (22), что функция Леверетта представляет собой отношение капиллярного давления pК, соответствующего различной степени насыщенности пор, к величине, пропорциональной среднему значению капиллярного давления, развиваемого менисками в порах со средним радиусом. Однако анализ показал, что предположение о вероятном совпадении зависимостей функция Леверетта — водонасыщенность Sв для всех пород на практике не оправдалась. На рис. для примера приведены зависимости J=f(Sв), полученные Н. С. Гудок, для различных пород продуктивных пластов нижнего мела прикумской нефтеносной области.
Легко установить по формулам (19) и (22), что функция Леверетта представляет собой отношение капиллярного давления pК, соответствующего различной степени насыщенности пор, к величине, пропорциональной среднему значению капиллярного давления, развиваемого менисками в порах со средним радиусом. Однако анализ показал, что предположение о вероятном совпадении зависимостей функция Леверетта — водонасыщенность Sв для всех пород на практике не оправдалась. На рис. для примера приведены зависимости J=f(Sв), полученные Н. С. Гудок, для различных пород продуктивных пластов нижнего мела прикумской нефтеносной области.
Рис. Зависимость функции Леверегга от водонасыщенности (по данным Н. С. Гудок). 1 — алевролиты; 2 — песчаники (пористость пород m =20—30 %, проницаемость k =0,05—0,3 мкм2.
Для корреляции зависимостей рк=f(Sв), полученных для различных пород, применяются также статистические методы.
9. ЛАБОРАТОРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПРОНИЦАЕМОСТИ ПОРОД
Проницаемость горных пород зависит от многих, факторов— горного давления в условиях их залегания, от температуры, степени взаимодействия флюидов с породой и т. д. Установлено, например, что газопроницаемость в атмосферных условиях существенно выше проницаемости пород даже для неполярных углеводородных жидкостей, практически не взаимодействующих с породой. Это объясняется частичным проскальзыванием газа вдоль поверхности каналов пористой среды вследствие незначительного внутреннего трения молекул газа (эффект Клинкенберга). По данным Н. С. Гудок, иногда проницаемость некоторых пород для газа при атмосферных условиях превышала их проницаемость при давлении 10 МПа в два раза.
Установлено, что с увеличением температуры среды газопроницаемость пород уменьшается, что связано с возрастанием скоростей движения молекул, уменьшением длины свободного их пробега и возрастанием сил трения вследствие интенсификации обмена количеством движения между отдельными слоями. По данным Н. G. Гудок, рост температуры с 20 до 90°С может сопровождаться уменьшением проницаемости пород на 20—30%.
Влияние на проницаемость пород давления, температуры, степени взаимодействия флюидов с породой и необходимость измерения проницаемости пород по газу и по различным жидкостям приводит к необходимости конструировать приборы, позволяющие моделировать различные условия фильтрации с воспроизведением пластовых давлений и температур.
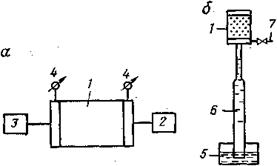 Поэтому для определения абсолютной проницаемости горных пород используются разнообразные приборы. Однако принципиальные схемы их устройства большей частью одинаковы — все они состоят из одних и тех же основных элементов: кернодержателя, позволяющего фильтровать жидкость и газы через пористую среду, устройств для измерения давления на входе и выходе из керна, расходомеров и приспособлений, создающих и поддерживающих постоянный расход жидкости или газа через образец породы (рис.). Различаются они лишь тем, что одни из них предназначены для измерения проницаемости при больших давлениях, другие — при малых, а третьи— при вакууме. Одни приборы используются для определения проницаемости по воздуху, другие по жидкости. Поэтому отдельные их узлы имеют соответственно различное конструктивное оформление.
Поэтому для определения абсолютной проницаемости горных пород используются разнообразные приборы. Однако принципиальные схемы их устройства большей частью одинаковы — все они состоят из одних и тех же основных элементов: кернодержателя, позволяющего фильтровать жидкость и газы через пористую среду, устройств для измерения давления на входе и выходе из керна, расходомеров и приспособлений, создающих и поддерживающих постоянный расход жидкости или газа через образец породы (рис.). Различаются они лишь тем, что одни из них предназначены для измерения проницаемости при больших давлениях, другие — при малых, а третьи— при вакууме. Одни приборы используются для определения проницаемости по воздуху, другие по жидкости. Поэтому отдельные их узлы имеют соответственно различное конструктивное оформление.
Рис. Схемы приборов для определения проницаемости пород: 1 - кернодержатель; 2 - расходомер; 3 - устройство, создающее постоянный расход жидкости или газа через керн; 4 - измерители перепада давления; 5 - сосуд с водой; 6 — стеклянная трубка; 7 — вентиль.
Кроме стационарных приборов, схема строения которых приведена на рис. а, для измерения проницаемости используются также упрощенные устройства. Схема одного из них приведена на рис. б. Образец в кернодержателе одной стороной соединен с атмосферной трубкой, конец которой опущен под уровень воды. Создав через вентиль 7 разрежение под керном, уровень воды в трубке поднимают на некоторую высоту. После закрытия этого вентиля фильтрация воздуха через керн осуществляется под действием переменного разрежения, характеризующегося высотой столба воды в трубке. Мерой проницаемости породы служит (при постоянстве размеров образца) время опускания мениска в трубке в заданном интервале.
На практике оказывается, что проницаемость для жидкости обычно почти всегда меньше, чем для газа. Лишь при высокой проницаемости пород значения ее примерно одинаковы для жидкости и газа. Уменьшение проницаемости одной и той же породы для жидкости по сравнению с проницаемостью для газа происходит вследствие разбухания глинистых частиц и адсорбции жидкости при фильтрации нефти и воды через породы. Поэтому абсолютную проницаемость пород принято определять с помощью воздуха или газа. Состав газа на проницаемость пород заметно влияет только при высоком вакууме (при так называемом кнудсеновском режиме течения газа, когда столкновения молекул редки по сравнению с ударами о стенки пор, т. е. когда газ настолько разрежен, что средняя длина пробега молекул сравнима с диаметром поровых каналов). В этих условиях проницаемость пород зависит от среднего давления, молекулярной массы газа и температуры и тем выше, чем меньше молекулярная масса и давление. В пластовых условиях проницаемость горных пород практически мало зависит от состава газа.
Как уже упоминалось, фазовые проницаемости, кроме степени насыщенности пористой среды различными фазами, зависят от ряда других факторов и специфических свойств конкретной пластовой системы. В результате фактические показатели иногда значительно отклоняются от расчетных. Поэтому при определении зависимости относительных проницаемостей от насыщенности следует проводить специальные опыты, поставленные с учетом специфических свойств исследуемой пластовой системы.
Устройство установок, применяемых для этих целей, более сложное, чем установок, рассмотренных ранее, так как необходимо моделировать многофазный поток, регистрировать насыщенность порового пространства различными фазами и расход нескольких фаз. Установки для исследования многофазного потока обычно состоят из следующих основных частей:
1) приспособления для приготовления смесей и питания керна;
2) кернодержателя специальной конструкции;
3) приспособления и устройства для приема, разделения и измерения раздельного расхода жидкостей и газа;
4) устройства для измерения насыщенности различными фазами пористой среды;
5) приборов контроля и регулирования процесса фильтрации.
Насыщенность порового пространства различными фазами можно определить несколькими способами: измерением электропроводности пористой среды, взвешиванием образца (весовой метод) и т. д. В первом случае измеряется электропроводность участка пористой среды, строится график, который сравнивается с тарировочной кривой (заранее составленной и представляющей собой зависимость электропроводности среды от содержания в порах различных фаз), затем определяется насыщенность порового пространства соответствующими фазами. Такой метод пригоден, если одна из жидкостей, используемых при исследовании, является проводником электричества (соленая вода, водоглицериновые смеси и т. д.).
При весовом методе среднюю насыщенность образца жидкостью и газом определяют по изменению его массы вследствие изменения газосодержания в поровом пространстве среды.
При движении многофазных систем проницаемость для каждой фазы определяется по следующим формулам:
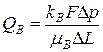 ;
; 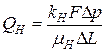 ;
;  (1.24)
(1.24)
Здесь QB, QH и QГ — соответственно расходы в единицу времени воды, нефти и средний расход газа в условиях образца; kB, kГ и kН — фазовые проницаемости для нефти, газа и воды; mв, mн и mг — соответственно динамические вязкости воды, нефти и газа; F — площадь фильтрации; Dр — перепад давления, DL — длина пористой среды.
Фазовые проницаемости рассчитываются также по результатам вытеснения из пористой среды одной фазы другой и по промысловым данным. Приближенно их можно оценить также по кривым распределения пор по размерам.
10. УДЕЛЬНАЯ ПОВЕРХНОСТЬ ГОРНЫХ ПОРОД
Удельная поверхность пород —суммарная поверхность частиц или поровых каналов, содержащихся в единице объема образца,— зависит от степени дисперсности частиц, из которых они слагаются. Вследствие небольших размеров отдельных зёрен песка и большой плотности их укладки поверхность порового пространства пласта может достигать огромных размеров, что значительно осложняет задачу полного извлечения нефти из породы.
Проницаемость, адсорбционная способность, содержание остаточной (реликтовой) воды и т. д. зависят от удельной поверхности нефтеносных пород. Работами советских ученых М. М. Кусакова, Б. В. Дерягина, К. А. Зинченко, Ф. А. Требина установлено, что кроме объемных свойств жидкостей и газов (например, плотности, вязкости) на характер фильтрации нефти влияют и молекулярные явления, происходящие на контактах жидкости и породы. Объемные свойства жидкостей (вязкость, плотность) обусловливаются действием молекул, распространенными внутри жидкой фазы. Поэтому в крупнозернистой породе с относительно небольшой удельной поверхностью молекулы, находящиеся на поверхности, почти не влияют на процесс фильтрации, так как их число весьма мало по сравнению с числом молекул, находящихся внутри объема жидкости. Если же пористая среда имеет большую удельную поверхность, то число поверхностных молекул жидкости возрастает и становится сравнимым с числом объемных молекул. Поэтому поверхностные явления в малопроницаемой породе могут оказать более значительное влияние на процесс фильтрации жидкости, чем в крупнозернистой.
Таким образом, удельная поверхность — одна из важнейших характеристик горной породы.
Следует отметить, что, несмотря на кажущуюся простоту понятия удельной поверхности, сложно точно определить ее величину. Дело в том, что поры в пористой среде представлены каналами размерами от десятков и сотен микрометров (по диаметру) до размеров молекул. Поэтому удельная поверхность глин, или других адсорбентов, влияющая на процесс адсорбции, не имеет для данного пористого вещества определенного значения, а зависит от размера адсорбируемых молекул. Только для молекул, имеющих одинаковые размеры, можно по опытным данным получить близкие значения удельных поверхностей одного и того же адсорбента.
У мелкопористых сред при адсорбции существенно отличающихся по размерам адсорбируемых молекул веществ наблюдаются значительные отклонения в размерах удельной поверхности (явление это носит название ультрапористости).
Легко установить, что если бы все частицы имели шарообразную форму (фиктивный грунт), то поверхность всех частиц в 1 м3 породы составила
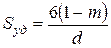
где Sуд — удельная поверхность, м2/м3; m — пористость, доли единицы; d — диаметр частиц, м.
Для естественных песков удельная поверхность вычисляется суммированием ее значения по каждой фракции гранулометрического состава
 (26)
(26)
Здесь Р — масса породы, кг; Рi —масса данной фракции, кг; di — средние диаметры фракций (в м), определяемые по формуле
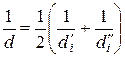 (27)
(27)
где d'i и d"i — ближайшие стандартные размеры отверстий сит.
По экспериментальным данным К. Г. Оркина, при определении удельной поверхности по механическому составу в формулу (26) следует ввести поправочный коэффициент а, учитывающий повышение удельной поверхности вследствие нешаровидности формы зерен (а =1,2—1,4). Меньшие значения а относятся к окатанным зернам, большие—к угловатым.
Используя уравнения, связывающие параметры фиктивного грунта, аналогичные формуле (25), можно также установить зависимость между удельной поверхностью и другими параметрами реальных пород. Для этого при выводе соответствующих формул реальный грунт с неоднородными частицами заменяют эквивалентным естественному фиктивным грунтом. При этом гидравлическое сопротивление фильтрации жидкости в обоих грунтах и удельная поверхность их должны быть одинаковыми. Диаметр частиц такого фиктивного грунта принято называть эффективным dэф. Сопоставляя формулы (25) и (26), можно видеть, что
 (28)
(28)
или 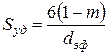 (29)
(29)
С другой стороны, удельную поверхность можно выразить через гидравлический радиус d:
 (30)
(30)
или 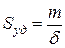 (31)
(31)
Гидравлический радиус, как известно, равен отношению площади порового канала к его периметру и для поры с круглым сечением радиусом R

Тогда можно написать 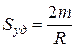 (32)
(32)
Подставляя в (32) значение R из формулы (18), получим
 (33)
(33)
где k — проницаемость, м2.
Если выразить проницаемость в мкм2, то получим удельную поверхность в м2/м3:
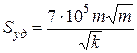 (34)
(34)
Из формул (33) и (34) следует, что чем меньше радиус поровых каналов и проницаемость породы, тем больше ее удельная поверхность.
Формула (34) представляет собой один из вариантов формул Козени— Кармана, устанавливающих зависимость коэффициента проницаемости от пористости, удельной поверхности и структуры порового пространства. В общем виде формула Козени — Кармана записывается в виде
 (35)
(35)
где Т — извилистость поровых каналов (отношение среднестатистической длины каналов к длине керна); j — структурный коэффициент, учитывающий форму поровых каналов. Значение извилистости Т может достигать 6 и более.
11. МЕТОДЫ ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ ПОВЕРХНОСТИ ГОРНЫХ ПОРОД
Кроме упомянутых способов определения удельной поверхности пород (по их гранулометрическому составу, по величине пористости и проницаемости), существуют следующие способы оценки этого параметра: фильтрационный, основанный на измерении сопротивления течению через пористое тело разреженного воздуха; адсорбционные, а также метод меченых атомов.
Методы определения удельной поверхности пористых сред, основанные на использовании пуазейлевского режима течения воздуха сквозь объект исследования [т. е. основанные на использовании формул типа (35)], применимы только для приближенной оценки поверхности грубозернистых однородных сред, ширина пор в которых намного больше длины свободного пробега молекул воздуха. При этом не нужно учитывать скольжения газа по стенкам пор. Движение газа в мелкодисперсной пористой среде существенно облегчается при скольжении молекул по стенкам пор, и сопротивление среды с высокой удельной поверхностью прохождению через нее газов иногда существенно меньше по сравнению с подсчитанными по формулам типа (35), не учитывающим скольжения газа по стенкам. Поэтому в данном случае можно использовать метод, основанный на измерении сопротивления течению через пористое тело разреженного воздуха при кнудсеновском режиме, имеющем скорее диффузионный характер. Кнудсеновский режим наступает, когда максимальные просветы пор становятся меньше длины свободного пробега молекул газа. В этом случае соударения молекул между собой становятся редкими (по сравнению с ударами о стенки пор). Зависимость молярной скорости течения газа от удельной поверхности и других параметров выражается равенством
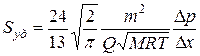 (36)
(36)
где Q — число киломолей воздуха, протекающего через 1 м2 поперечного сечения пористой среды толщиной Dх (в м) за 1 с при перепаде давления Dр (в Па); М — относительная молекулярная масса воздуха, кг/кмоль; R — универсальная газовая постоянная, Дж/(кмоль-градус); Т —температура опыта, °С.
Для определения удельной поверхности пористых тел по результатам измерения кнудсеновского режима фильтрации сконструированы специальные приборы.
Горные породы, слагающие пласт, заполнены жидкой средой—водой и нефтью. Удельная поверхность (например, глин и некоторых других пород) под действием водной среды может изменяться, и «сухие» способы ее измерения не всегда соответствуют действительным условиям залегания пород в естественных условиях.
Удельную поверхность пористых сред в водной среде обычно определяют методом адсорбции красителей или методом поверхностного обмера при помощи радиоактивных индикаторов. Площадь поверхности минералов Sуд при этом рассчитывают по числу молекул радиоактивного индикатора, поглощенных пористой средой, и по площади, приходящейся на один атом данного радиоактивного вещества на поверхности кристалла:
Sуд = атwN, (37)
где ат — число молей (атомов) вещества, связанного с 1 г твердой фазы; w —площадь, приходящаяся на один атом данного вещества на поверхности кристалла (значение ее известно для многих веществ); N — число Авогадро.
Количество радиоактивного иона, поглощенного веществом при его погружении в раствор, определяется по уменьшению активности фильтрата раствора вследствие поглощения меченого атома твердой фазой.
Особое место по точности занимает адсорбционный метод вследствие того, что поверхность пористой среды промеряется такими малыми объектами, как молекулы адсорбируемого вещества, выстилая ими поверхность пористой среды. По количеству адсорбированного вещества (т. е. по числу его молекул) и площади, приходящейся на один атом данного вещества, вычисляется удельная поверхность пористой среды.
При адсорбционных методах исследования удельной поверхности пористых сред необходимы сложная аппаратура, высококвалифицированные исполнители. Поэтому в лабораториях физики нефтяного пласта эта поверхность пород обычно оценивается фильтрационными методами.
По результатам измерений Ф. И. Котяхова удельная поверхность кернов изменяется от 38000 до 113000 м2/м3.
12.
13. КОЛЛЕКТОРСКИЕ СВОЙСТВА ТРЕЩИНОВАТЫХ ПОРОД
Вследствие совершенствования методов исследования коллекторов нефтяных месторождений и накопления богатого промыслового материала в последние годы стало известно, что во многих залежах коллекторские свойства пластов характеризуются не только обычной межзерновой пористостью, но в значительной степени также и наличием трещин.
Иногда емкость коллектора и промышленные запасы нефти в нем определяются преимущественно объемом трещин.
Залежи, связанные с трещиноватыми коллекторами, приурочены большей частью к плотным карбонатным породам, а в некоторых районах (Восточные Карпаты, Иркутский район и др.) и к терригенным отложениям. Пласты этих месторождений сложены плотными породами, очень часто неспособными практически фильтровать сквозь себя жидкости (т. е. обладающими низкой межзерновой проницаемостью). Вместе с тем из них получают значительные притоки нефти к скважинам, что обеспечивается наличием разветвленной сети трещин, пронизывающих эти коллекторы.
Существуют различные мнения о том, что составляет емкость трещиноватого коллектора. Иногда емкость такого коллектора определяется только объемом трещин. В большинстве же случаев она обусловливается пустотами трех видов.
1. Межзерновым поровым пространством. Пористость 2— 10 %.
2. Кавернами и микрокарстовыми пустотами. Пористость, слагаемая пустотами этого вида, характерна для карбонатных пород, где она составляет значительную часть (13—15 %) полезной емкости трещиноватого коллектора.
3. Пространством самих трещин, составляющих трещинную пористость. Пустоты этого вида составляют десятые и сотые доли процента относительно объема трещиноватой породы. Пока известно мало залежей, где трещинная емкость пород оказалась бы соизмеримой с объемом добываемой из них нефти. Чаще всего трещины, по-видимому, играют в основном роль путей фильтрации нефти и газа, связывающих воедино межзерновое пространство блоков, пустоты каверн и микрокарстов.
Исходя из основных коллекторских свойств, обусловливающих емкость и пути фильтрации в трещиноватых коллекторах, последние можно подразделить на следующие основные виды.
1. Коллекторы кавернозного типа. Емкость пород слагается из полостей каверн и карстов, связанных между собой и скважинами системой микротрещин. Приурочены в основном к карбонатным породам. Фильтрация жидкостей и газов в них осуществляется по микротрещинам, соединяющим мелкие каверны.
2. Коллекторы трещинного типа. Емкость коллектора определяется в основном трещинами. Коллекторы такого типа приурочены к карбонатным породам, а также к плотным песчаникам, хрупким сланцам и другим плотным породам. Фильтрация нефти и газа происходит только по системам микротрещин с раскрытостью свыше 5—10 мкм. Такие виды коллекторов мало распространены.
3. Коллекторы смешанные, представляющие собой сочетания и переходы по площади и по разрезу трещиноватого или кавернозного коллекторов с нормальными. Коллекторы этого вида широко распространены.
Установлено, что закономерности развития трещиноватости в горных породах связаны с тектоникой и направлением дизъюнктивных дислокаций и трещиноватость, как правило, выражена правильными геометрическими системами трещин.
По результатам исследований Е. М. Смехова и других, сеть трещин обычно состоит из двух основных систем вертикальных нарушений сплошности, обладающих двумя взаимно перпендикулярными направлениями. Иногда сетка представляется одной системой горизонтальных трещин по отношению к плоскостям напластования (тонкослоистые и сланцеватые породы) или системой трещин с различной ориентацией (глины). Значительная же часть систем трещин имеет падения, близкие к вертикальным (относительно слоистости пород).
Часто наблюдается ориентированность трещиноватости по странам света. Простирание систем трещиноватости в общем согласуется с основным направлением крупных тектонических деформаций! В отдельных районах основные системы трещиноватости совпадают по всей толще осадочных пород независимо от их возраста.
Все это дает основание полагать, что ориентированность проницаемости отдельных участков продуктивных пластов относительно залежи, по-видимому, объясняется наличием ориентированной системы трещин и зависимостью между направлениями основных систем трещиноватости и простиранием складок. Это подтверждается совпадением линий, соединяющих скважины с относительно большими дебитами, с направлением простирания основных систем трещиноватости.
Обычно строгой закономерности в распределении систем трещиноватости по элементам структур, к которым приурочены нефте- и газосодержащие залежи, не наблюдается, так как предполагается, что, кроме тектонического фактора, на распределение систем трещин на структуре влияют в некоторой степени и свойства самих пород. Вообще же наиболее трещиноваты те участки структуры, где изменяются углы падения пород — периклинали на пологих складках и своды на структурах с крутыми крыльями.
О раскрытии трещин на глубине также существуют различные мнения. В шахтах, по сравнению с нефтяными скважинами, имеющими незначительную глубину, иногда встречаются трещины с раскрытостью до 10 см (шахты Норильского района и Ухты, озокеритовые месторождения Борислава). Большинство исследователей, однако, считают, что при значительных величинах горного давления на больших глубинах зияющие трещины не могли сохраниться. По результатам исследования ВНИГРИ, раскрытость трещин нефтесодержащих пластов обычно составляет 10-20 мкм, и лишь иногда она возрастает до 30 мкм. В породах же, подверженных процессам растворения и перекристаллизации минералов, встречаются каверны и карсты значительных размеров. Так, например, при бурении скважин на месторождении Надьлендел в Венгрии наблюдались провалы инструмента в карбонатных коллекторах до 2— 3 м на глубинах около 3000 м.
Методика исследования коллекторских свойств трещиноватых горных пород имеет свои особенности. Их качества как коллектора характеризуются густотой и раскрытостью трещин, которые определяют трещинную пористость и проницаемость, обусловленную наличием в породе трещин.
Здесь следует подчеркнуть, что понятие «раскрытость» включает в себя некоторую условность. Существование трещин на больших глубинах в условиях проявления горного давления возможно только при многочисленных контактах между стенками трещины. Площадь контактов по сравнению с поверхностью стенки мала, и поэтому наличие их существенно не влияет на емкость и фильтрационные свойства трещин. На этом основании вводят понятие раскрытости трещин как преобладающей величины расстояний стенок трещин между контактами.
Уже отмечалось, что подавляющее большинство трещин, по-видимому, имеет тектоническое происхождение и объединяется в ориентированные системы. Поэтому далее будем рассматривать трещиноватость, характеризующуюся системами трещин, стенки которых можно принять за плоскости.
Исследованиями Е. М. Смехова и других установлено, что интенсивность трещиноватости зависит от литологических свойств пород. Трещиноватость карбонатных пород обычно больше, чем аргиллитов и песчано-алевритовых пород, песчаников и солей.
Раскрытость трещин также зависит от литологического состава пород и их происхождения. Раскрытость трещин различных пород колеблется в пределах 14—80 мкм.
Интенсивность трещиноватости горной породы, рассеченной совокупностью трещин, характеризуется объемной Т и поверхностной Р плотностью трещин, которые определяются следующими соотношениями:
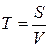 ,
, 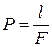 (38)
(38)
где S — площадь половины поверхности всех стенок трещин, секущих объем V породы; l — суммарная длина следов всех трещин, выходящих на поверхность площадью F.
Мерой трещиноватости породы одной системы трещин служит густота трещин Г, представляющая собой отношение числа трещин Dn, секущих нормаль их плоскостей, к элементу длины DL этой нормали:
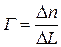 (39)
(39)
Для однородной трещиноватости, т. е. когда трещины находятся на равном расстоянии друг от друга, густота трещин
 , (40)
, (40)
где L — расстояние между трещинами в системе.
 Объемная плотность Т характеризует трещиноватость с любой геометрией пласта. Очевидно, поверхностная плотность Р зависит от ориентации площади измерения (рис. линия 2) относительно направления трещин (рис., линия 1), а густота Г их характеризует только выделенную систему трещин.
Объемная плотность Т характеризует трещиноватость с любой геометрией пласта. Очевидно, поверхностная плотность Р зависит от ориентации площади измерения (рис. линия 2) относительно направления трещин (рис., линия 1), а густота Г их характеризует только выделенную систему трещин.
Плотность трещиноватости пород может изменяться в широких пределах. Объемная плотность трещин девонских отложений Южно-Минусинской впадины (по наблюдениям в обнажениях на дневной поверхности), например, изменяется в пределах 9-60 1/м.
Между Т, Р и Г существует следующая связь:

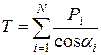
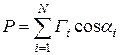 (41)
(41)
где N — число систем трещин; ai — угол между перпендикуляром к плоскости i -й системы трещин и площадкой, на которой измеряется величина Р (см. рис.).
Трещинная пористость для одной системы трещин
mTi=biГi (42)
где bi — раскрытость трещин. Для системы трещин имеем
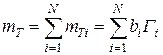 (43)
(43)
При bi = const= b
mT=bT (44)
Зависимость проницаемости пород от трещинной пористости и раскрытия трещин можно получить при помощи уравнения Буссинеска, согласно которому расход жидкости, приходящийся на единицу протяженности щели,
 (45)
(45)
где b — раскрытие трещины; m — динамическая вязкость жидкости; dp/dx — градиент давления.
Следовательно, расход жидкости через площадь фильтрации породы
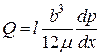 (46)
(46)
Приняв действительным равенство mT=bl/T, получим
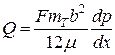 (47)
(47)
По закону Дарси расход жидкости через эту же породу
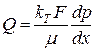 (48)
(48)
Здесь kT — проницаемость трещин.
Приравнивая правые части уравнений (47) и (48), получим
kT = 85000 b 2 mT, (49)
где b — раскрытие трещины, мм; kT — проницаемость, мкм2; mT — трещинная пористость, доли единицы.
 Формула (49) действительна для случая, когда трещины перпендикулярны к поверхности фильтрации. В действительности трещины могут, располагаться, произвольно, в результате чего проницаемость трещиноватой породы будет зависеть от простирания их систем и направления фильтрации. Поэтому важно знать ориентированность трещин. Она определяется известными методами фиксации положения плоскости в пространстве — по азимуту падения d и углу падения w или же по направляющим косинусов единичного вектора нормали к плоскости трещины (cos a 1, cos a 2, cos a 3, где a1 a2 и a3 — углы между единичным вектором и осями координат, рис.).
Формула (49) действительна для случая, когда трещины перпендикулярны к поверхности фильтрации. В действительности трещины могут, располагаться, произвольно, в результате чего проницаемость трещиноватой породы будет зависеть от простирания их систем и направления фильтрации. Поэтому важно знать ориентированность трещин. Она определяется известными методами фиксации положения плоскости в пространстве — по азимуту падения d и углу падения w или же по направляющим косинусов единичного вектора нормали к плоскости трещины (cos a 1, cos a 2, cos a 3, где a1 a2 и a3 — углы между единичным вектором и осями координат, рис.).
Рис. Ориентирование плоскости трещин в пространстве.
В общем случае, если трещины располагаются произвольно, а проницаемость рассчитывается для любого горизонтального направления фильтраций, то формула для расчета проницаемости имеет вид
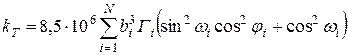 (50)
(50)
где bi и Гi — раскрытость и густота трещин соответственно в см и 1/см; w i — угол падения трещин данной системы; ji — угол между задаваемым направлением фильтрации и простиранием данной системы трещин.
Параметры трещиноватости находят также по керновому материалу и по шлифам. При микроскопическом исследовании шлифа определяются раскрытие трещин, их протяженность и площадь шлифа. Параметры трещиноватых пород подсчитывают по формулам
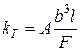 (51)
(51)
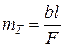 (52)
(52)
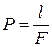 (53)
(53)
Здесь kT — трещинная проницаемость, мкм2; А — численный коэффициент, зависящий от геометрии систем трещин в породе (для трех взаимно перпендикулярных систем трещин A =2,28×106; для хаотически расположенных трещин А =1,7×106); l — протяженность трещин в шлифе, см; F — площадь шлифа, см2; mT —трещинная пористость, доли единицы; Р — поверхностная плотность трещин.
Для определения параметров трещиноватости используются геологические, геофизические и гидродинамические методы исследования трещиноватых пород.
При геологических методах получают достоверные сведения о плотности трещин и их ориентированности по данным исследования трещиноватости пород в их обнажениях на дневной поверхности, а также в шахтах и других горных выработках. Раскрытость же поверхностных трещин подвержена влиянию эрозии.
Геофизические методы исследования трещиноватых коллекторов основаны на зависимости свойств потенциальных полей (электрических, гравитационных, упругих и т. д.) от параметров трещиноватости. Эти методы находятся в стадии развития и становления. Все более широко применяют гидродинамические методы, основанные на использовании результатов исследования скважин. Показатели работы скважин (зависимость дебита от забойного давления, скорость восстановления давления в остановленной скважине и т. д.) зависят от параметров трещиноватости коллектора. Эти методы подробно излагаются в курсах разработки и эксплуатации нефтяных и газовых месторождений.
Многочисленные измерения показывают, что трещинная пористость от общей пористости трещиноватой породы обычно не превышает 1 % и часто бывает менее 0,1 %. В противоположность этому проницаемость трещинного коллектора обычно определяется пропускной способностью трещин, ибо трещинные коллекторы, как правило, связаны с плотными и хрупкими породами, межзерновая проницаемость блоков которых редко превышает 0,1 мкм2.
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 3711; Нарушение авторских прав?; Мы поможем в написании вашей работы!