
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В массиве
|
|
|
|
НАПРЯЖЕННОЕ СОСТОЯНИЕ ПОРОД В УСЛОВИЯХ ЗАЛЕГАНИЯ
Породы, залегающие в недрах земли, находятся под влиянием горного давления, которое обусловливается весом пород, тектоническими силами, пластовым давлением и термическими напряжениями, возникающими под влиянием тепла земных недр. В результате воздействия на породу комплекса упомянутых сил элемент (кубик) породы, выделенный из массива, может находиться в общем случае в условиях сложного напряженного состояния, характеризующегося тем, что результирующие векторы напряжений, действующих на грани, не являются перпендикулярными к его граням. Разлагая эти результирующие векторы по направлению ортогональных осей, 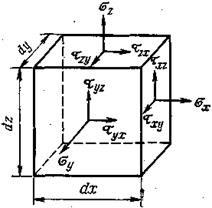 можно представить, что на каждой плоскости кубика будут действовать (рис.) по три компоненты напряжений — одна нормальная s, направленная перпендикулярно к грани кубика, и две касательные τ, действующие касательно к поверхности грани кубика. Учитывая, что выделенный элементарный кубик находится в равновесии, касательные напряжения, направленные противоположно друг другу в одной плоскости, должны быть равны, так как суммарный момент действующих на кубик сил равен нулю,
можно представить, что на каждой плоскости кубика будут действовать (рис.) по три компоненты напряжений — одна нормальная s, направленная перпендикулярно к грани кубика, и две касательные τ, действующие касательно к поверхности грани кубика. Учитывая, что выделенный элементарный кубик находится в равновесии, касательные напряжения, направленные противоположно друг другу в одной плоскости, должны быть равны, так как суммарный момент действующих на кубик сил равен нулю,
τух=τxy τxz=τzx τyz=τzy
Рис. 1. Компоненты напряжений, действующих в элементе породы
Компоненты напряжений зависят от ориентации выделенного элементарного объема породы в пространстве. Его можно ориентировать таким образом, что касательные напряжения будут равными нулю и напряженное состояние выделенного элемента будет характеризоваться только нормальными составляющими. Они в этом случае называются главными нормальными напряжениями, а грани, на которые они действуют, называют главными плоскостями.
Нормальные и касательные напряжения, действующие на элемент породы, вызывают соответствующие деформации era граней. Нормальные составляющие напряжений вызывают деформации сжатия элемента или растяжения εx, εу и εz, а касательные напряжения — деформации сдвига граней gху, gyz, gxz (деформация сдвига обычно измеряется углами сдвига, так как из-за малости их величины tgg=g). Суммарная деформация граней, gху, gyz, gxz — величина, на которую уменьшается прямой угол между соответствующими гранями в результате сдвига. Каждый из них является следствием проявления и наложения друг на друга двух бесконечно малых сдвигов от двух пар касательных напряжений, стремящихся вращать элемент в противоположные стороны.
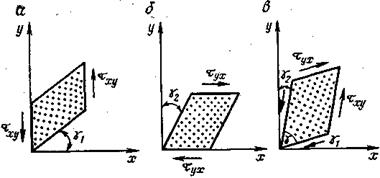 Для примера на рис. 2 приведена схема проявления касательных напряжений в случае чистого сдвига грани ху (т. е. когда по внешним граням элемента отсутствуют нормальные напряжения).
Для примера на рис. 2 приведена схема проявления касательных напряжений в случае чистого сдвига грани ху (т. е. когда по внешним граням элемента отсутствуют нормальные напряжения).
Рис. 2. Схема деформаций грани ху под влиянием касательных напряжений (чистый сдвиг)
На рис. 2,а показан сдвиг грани элемента при влиянии одной пары касательных напряжений τ xy с углом сдвига g1, а на рис. 2,б — сдвиг g2 под влиянием другой пары τyх. В результате наложения этих сдвигов деформация грани будет иметь вид, изображенный на рис. 2, в. В результате сдвига прямой угол грани уменьшится на сумму этих углов
gху=g1+g2
Если породы однородны и изотропны, то g1=g2=g. При этом суммарный угол сдвига составит
gху= 2g. (1)
В случае полностью изотропного тела связь между напряжениями и деформациями можно выразить следующими уравнениями, которые согласно закону Гука имеют вид
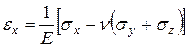 , (2)
, (2)
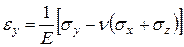 , (3)
, (3)
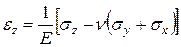 , (4)
, (4)
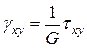 , (5)
, (5)
 (6)
(6)
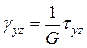 (7)
(7)
где Е — модуль продольной упругости (модуль Юнга); n — коэффициент Пуассона; G — модуль сдвига.
В пределах упругих деформаций между этими упругими характеристиками однородных изотропных материалов существуют следующие зависимости:
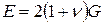 ;
; 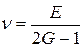 ;
; 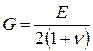 ;
; 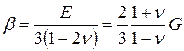 (8)
(8)
Здесь b — модуль объемного (всестороннего) сжатия, который выражает связь между давлением и относительным изменением объема D V/V материала.
Модуль Юнга Е для большей части горных пород изменяется от 109 до 1011 Па, а коэффициент Пуассона n — от 0 до 0,5.
Практическое изучение напряженного состояния горных пород в условиях их естественного залегания осложняется анизотропией их свойств, проявлением трещиноватости, большим разнообразием механических и физических свойств пород, входящих в массив, зависимостью упругих характеристик пород, (Е, n, G и b) от давления, температуры, влажности и т. д. По этой причине пока нет достаточно обоснованной единой теории, описывающей напряженное состояние горных пород. И задачи из этой области с применением теории упругости обычно решаются для частных случаев. При этом результаты относятся лишь к частным конкретным геологическим условиям.
Некоторые данные о значениях главных напряжений в нетронутом массиве (sх, sу и sz) получены в процессе горных работ.
До нарушения условий залегания пород скважиной внешнее давление от действия собственной массы вышележащих пород, и возникающие в породе ответные напряжения находятся в условиях равновесия.
Составляющие этого нормального поля напряжений имеют следующие значения.
По вертикали sz=rgH,
где sz — вертикальная составляющая напряжений; r - плотность породы; g — ускорение свободного падения; Н — глубина залегания пласта.
По горизонтали (в простейшем случае)
sy = sx = nrgH,
где n — коэффициент бокового распора.
Значение n для пластичных и жидких пород типа плывунов равно единице (тогда напряжения определятся гидростатическим законом), а для плотных и крепких пород в нормальных условиях, не осложненных тектонически, выражается во многих случаях долями единицы.
Коэффициент бокового распора и горизонтальное напряжение приближенно оценивают предполагая, что в процессе осадконакоплёния происходило только сжатие пород в вертикальном направлении, а в горизонтальном направлении деформаций не было (εх = εу = 0).
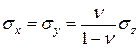 . (10)
. (10)
т. е. коэффициент бокового распора
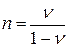 (11)
(11)
тогда 0< n <0,5. При выполнении упомянутых условий горизонтальные напряжения в породах меньше вертикальных, что, по-видимому, часто имеет место при небольшой глубине залегания, если в разрезе нет пород с пластическими свойствами. В случае пластичных и текучих горных пород n =1, для хрупких пород значения n составляют 0,3—0,7.
Формула (10) выведена для условия, когда справедливо предположение об отсутствии деформации пласта в горизонтальном направлении и когда не учитывается пластичность горных пород. В условиях реальных пластов эти предположения не всегда справедливы, и в них поэтому возможны более сложные напряженные состояния горных пород.
При достаточно больших давлениях на значительных глубинах (2500—3000 м), по-видимому, происходит выравнивание напряжений вплоть до величин, определяемых гидростатическим законом, так как предполагается, что за длительные геологические периоды породы испытывают пластические или псевдопластические деформации. Однако чаще всего вследствие интенсивных тектонических процессов, происходивших в земной коре в течение геологических периодов, горные породы многократно деформировались, что, по-видимому, сопровождалось возникновением значительных различий между главными напряжениями. В областях, где в результате тектонических процессов происходили боковое сдавливание пород и образование надвига, наибольшим должно быть горизонтальное напряжение, которое, по-видимому, может иногда в 2—3 раза превышать вертикальное горное давление. В зонах возникновения сбросов, не сопровождавшихся боковым сжатием, вертикальные напряжения пород должны значительно превышать горизонтальные.
Для изучения напряженного состояния горных пород применяются аналитические, лабораторные методы и натурные исследования. Лабораторные и производственные исследования осуществляются с помощью специальной аппаратуры и приборов. Важным преимуществом производственных методов изучения напряженного состояния пород является измерение напряжений в естественных условиях залегания и возможность непосредственного применения результатов опытов для решения задач практики. Один из широко распространенных способов — измерение напряжений и деформаций горных пород внутри скважины (пробуренной в массиве) с помощью деформометров и датчиков напряжений. Перспективны геофизические методы, которые основаны на зависимости скорости распространения упругих колебаний в породах, зависимости удельного сопротивления и других физических свойств пород от их напряженного состояния.
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 943; Нарушение авторских прав?; Мы поможем в написании вашей работы!