Примеры решения задач на тему. «Основы термодинамики»

«Основы термодинамики»

Задача 1. Двухатомный идеальный газ (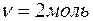) нагревают при постоянном объеме до температуры 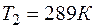. Определить количество теплоты, которое необходимо сообщить газу, чтобы увеличить его давление в 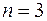раза.

Дано: ;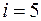

;

;

;

_____________

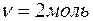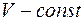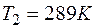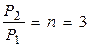
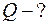
Решение.

Количество теплоты 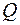, поглощаемое газом при изохорическом процессе, определяется по формуле:

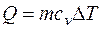, (1)

где 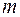- масса нагреваемого газа;

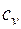- удельная теплоемкость газа при постоянном объеме;

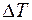- величина изменения температуры газы.

Известно, что .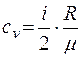

Для двухатомного газа

, .

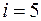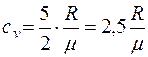Подставив выражение 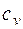в формулу (1), получим

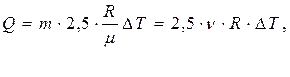(2)

где 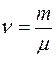- количество вещества ( 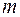- масса газа, - молярная масса газа).

Запишем уравнение Менделеева-Клапейрона для двух состояний идеального газа:

, (3)

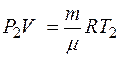(4)

По условию задачи 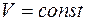, процесс изохорический.

Разделим (4) на (3), имеем (закон Шарля):

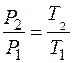; (5)

По условию задачи 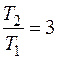, следовательно, ;

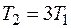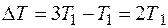; (6)

С учетом полученного значения 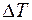по формуле (2) вычисляем значение количества теплоты, сообщенное газу:

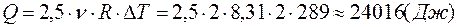
Проверка размерности расчетной формулы:

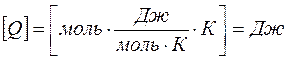
Ответ: количество теплоты, которое необходимо сообщить газу,

равно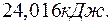

Задача 2. Во сколько раз необходимо увеличить объем 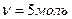идеального газа при изотермическом расширении, если его энтропия увеличилась на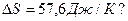

Дано: ;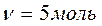

_____________________

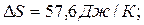
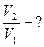
Решение.

Так как процесс изотермический, то в выражении энтропии 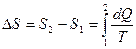температуру выносим за знак интеграла, получим:

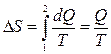. (1)

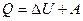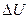Количество теплоты Q, полученное газом, найдем по первому началу термодинамики: , где - изменение внутренней энергии газа;

A – работа совершаемая газом против внешних сил. Для изотермического процесса 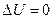, следовательно,

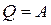; (2)

Работу газа при изотермическом процессе определяем по формуле

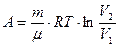; (3)

С учетом (2) и (3) равенство (1) примет вид:

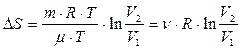, (4)

где - число молей газа;

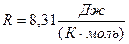- молярная газовая постоянная.

Из (4) получаем: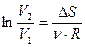

Проверяем размерность: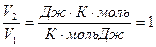

Вычисление: 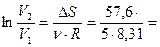1,386282;

.

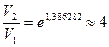Ответ: объем необходимо увеличить в 4 раза.

Задача 3. Тепловая машина работает по обратимому циклу Карно (рис.3). Температура теплоотдатчика 500⁰K. Определить термический КПД цикла и температуру теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу 350 Дж.

Дано:

T₁ = 500⁰K

Q₁ = 1кДж ^.= 10³ Дж

A = 350 Дж

_______________

h -? T₂ -?

Рис.3

Решение.

Термический КПД тепловой машины показывает, какая доля теплоты, полученная от теплоотдатчика, превращается в механическую работу. Термический к.п.д. выражается формулой:

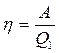(1)

где Q₁ - теплота, полученная от теплоотдатчика; А - работа, совершенная рабочим телом тепловой машины.

Зная КПД цикла, можно из формулы

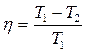(2)

определить температуру охладителя T₂ (теплоприемника)

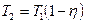(3)

Произведем вычисления:

h = 350 / 1000 = 0,35;

.

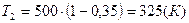Ответ: термический КПД тепловой машины равен 35%;

Температура теплоприемника равна 325 К.

Задача № 4. Определит изменение энтропии 14 г азота при изобарном нагревании его от 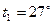до .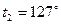

Дано: ;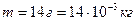

; ;

; ;

.

______________________________

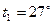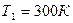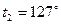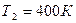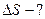
Решение.

Изменение энтропии

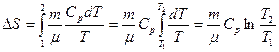, (1)

где 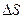изменение энтропии газа при постоянном давлении;

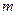- масса газа;

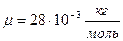- молярная масса азота;

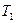и 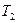- термодинамические температуры газа в первом и втором состоянии соответственно;

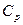- молярная теплоемкость газа при постоянном давлении

Молярная теплоемкость газа при постоянном давлении

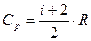, (2)

где i - число степеней свободы; т.к. молекула азота состоит из двух атомов, ;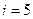

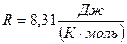- молярная газовая постоянная.

Подставляем (2) в (1), получаем:

;

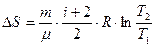Вычисление: .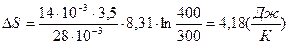

Проверка размерности расчетной формулы:

.

Ответ: изменение энтропии равно .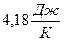

Дата добавления: 2014-11-07