И электромагнитных) и его решение

Вынужденных колебаний (механических

Дифференциальное уравнение

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t),изменяющего по гармоническому закону:

Если рассматривать механические колебания, то роль X(t)играет внешняя вынуждающая сила

F=F₀ cos w t. (147.1)

С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде

mх̈ = - kx – rx + F₀ cos wt.

Используя (142.2) и (146.10), придем к уравнению

(147.2)

Если рассматривать электрический колебательный контур, то роль X(t)играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение

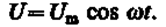(147.3)

Тогда уравнение (143.2) с учетом (147.3) можно записать в виде

Используя (143.4) и (146.11), придем к уравнению

(147.4)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференциальному уравнению

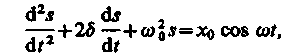(147.5)

применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x₀в случае механических колебаний равно F₀/m, в случае электромагнитных — U_m/L).

Решение уравнения (147.5) равно сумме общего решения (146.5) однородного уравнения (146.1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме (см. § 140). Заменим правую часть уравнения (147.5) на комплексную величину

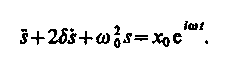(147.6)

Частное решение этого уравнения будем искать в виде

Подставляя выражение для s и его производных (s = ihs₀e^iht, s̈ = - h²s₀e^iht) в уравнение (147.6), получаем

(147.7)

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h = w. Учитывая это, из уравнения (147.7) найдем величину s₀и умножим ее числитель и знаменатель на

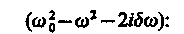
Это комплексное число удобно представить в экспоненциальной форме:

где

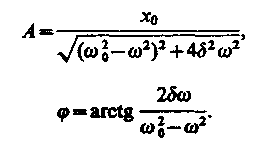(147.8) (147.9)

Следовательно, решение уравнения (147.6) в комплексной форме примет вид

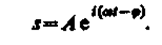
Его вещественная часть, являющаяся решением уравнения (147.5), равна

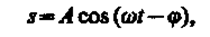(147.10)

где А и jзадаются соответственно формулами (147.8) и (147.9).

Таким образом, частное решение неоднородного уравнения (147.5) имеет вид

(147.11)

Решение уравнения (147.5) равно сумме общего решения однородного уравнения

(147.12)

(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой со и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.

Рис. 209

Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что w²₀ = l/(LC) (см. (143.4)) и d = R/(2L)(см. (146.11)):

(147.13)

Продифференцировав Q = Q_mcos(wt - a) no t, найдем силу тока в контуре при установившихся колебаниях:

(147.14) (147.15)

Выражение (147.14) может быть записано в виде

где j = a - p/2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)

(147.16)

Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (j > 0), если wL > 1/(w₀С),и опережает напряжение (j < 0), если wL < l(wC).

Формулы (147.15) и (147.16) можно также получить с помощью векторной диаграммы. Это сделано в § 149 для переменных токов.

Дата добавления: 2014-11-07