Примеры решения задач. Задача 1.3. Два корабля двигаются со скоростями и под углом

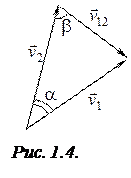Задача 1.3. Два корабля двигаются со скоростями 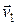и под углом 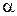один относительно другого. Найти скорость первого корабля относительно второго (рис. 1.4).

Решение. Найдем относительную скорость

.

По теореме косинусов имеем

.

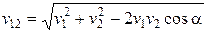Направление 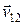определим углом 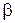с помощью теоремы синусов

.

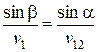Откуда

Задача 1.5. Для материальной точки, движущейся по оси ОХ, зависимость координаты от времени выражается уравнением:

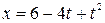, (1)

в котором все величины заданы в единицах СИ. Определить через t ₁ = 5 с после начала движения координату точки, ее скорость и пройденный путь.

Решение. В случае движения с постоянным ускорением уравнение для координаты имеет вид

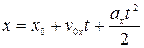, (2)

а для проекции скорости

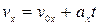^. (3)

Сравнивая уравнения (1) и (2), находим: х ₀ = 6 м, v _{0 х} = –4 м/с, а_х = 2 м/с². Затем, согласно уравнению (3), имеем

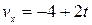. (4)

Найдем координату точки и ее скорость в момент времени t ₁ = 5 с, подставив это значение времени в уравнения (1) и (4):

,

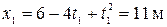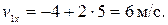
Мы видим, что v _0х < 0, a v _{1 x} > 0. Следовательно, точка сначала двигалась в направлении, противоположном направлению оси ОХ, а с некоторого момента времени t ₂ стала двигаться в обратную сторону. В этот момент проекция скорости на ось ОХ равна нулю. Согласно уравнению (4), получим 0 = –4 + 2 t ₂, откуда t ₂ = 2 с. Координата точки в этот момент времени

.

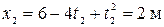Как видно из рисунка 1.5, путь

.

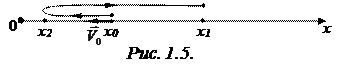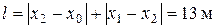Задача 1.10. Кабина лифта поднимается на протяжении первых 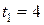с равноускоренно, при этом достигает скорости 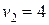м/с. С этой скоростью кабина движется на протяжении 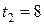с, а последние 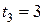с она движется равнозамедленно и останавливается. Определить перемещение кабины лифта. Построить графики скорости, пути и ускорения.

Решение. Ось 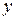направим вертикально вверх, начало координат расположим в точке, где находилась кабина в начальный момент времени. Рассмотрим движение кабины на трех участках.

На первом участке тело прошло

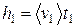, (1)

где 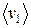– средняя скорость на этом участке. Поскольку движение равноускоренное, то

.

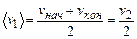Тогда уравнение (1) принимает вид

.

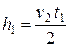На втором и третьем участках перемещения соответственно равняются

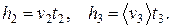
Поскольку 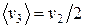, то

.

Тогда полное перемещение, которое осуществила кабина лифта, равняется

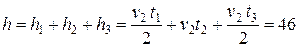м.

Ускорение на первом участке можно найти по формуле

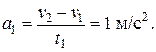
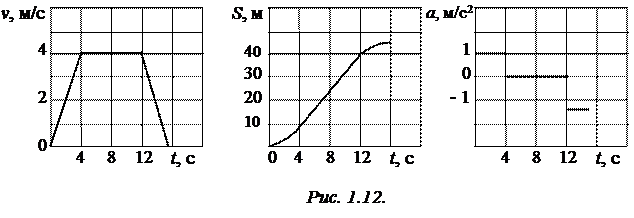Аналогично для второго и третьего участков ускорения равны соответственно 0 и -4/3 м/с².

Построим графики скорости, перемещения и ускорения, рассматривая каждый участок движения отдельно (рис. 1.12).

Дата добавления: 2014-11-07