Розділ 2. Правила наближених обчислень

Висновки

Під час виконання лабораторної роботи студент повинен навчитися не тільки виконувати вимірювання і обчислення шуканих величин за робочими формулами, але і осмислювати одержані результати.

Висновки не повинні бути простим констатуванням факту: “Я вивчив такі-то питання”, “Я виміряв таку величину” і т.п. Висновки повинні підкреслювати певну фізичну закономірність і ґрунтуватися на тих результатах, які одержані під час виконання роботи. Отже, висновки треба писати тільки тоді, коли в роботі виконується певне дослідження.

Приклад 1. В роботі ставиться задача визначення коефіцієнта в’язкості рідини. Студент одержує певний результат для деякої рідини, наприклад, для гліцерину. Ясно, що після закінчення роботи ніяких висновків зробити неможливо.

Приклад 2. В роботі ставиться задача дослідити залежність коефіцієнта в’язкості рідини від температури. Зробивши низку вимірювань коефіцієнта в’язкості рідини, студент осмислює одержані результати і в короткій формі формулює одержану залежність.

При цьому треба бути дуже обережними. Покажемо це на прикладі.

Деяка фізична залежність описується синусоїдою (рис. 8).

Якщо ми досліджуємо цю залежність в інтервалі (0... а), то можемо зробити висновок, що шукана величина “ y ” зі збільшенням “ х ” монотонно зростає. Досліджуючи цю залежність в інтервалі (а.. .в) – ми повинні відмітити монотонне зменшення шуканої величини “ y ” зі зростанням величини “ х ”.

Отже, якщо ми хочемо сформулювати характер деякої фізичної залежності y = f (x), треба максимально конкретизувати величину “ y ” і обов’язково вказувати інтервал, в якому змінювалася величина “ х ”.

1. Наближені обчислення. Виконуючи обчислення, слід пам'ятати про ту точність яку треба, або можна одержати. Вкрай неприпустимо вести обчислення з великою точністю, коли дані задачі не дозволяють або не вимагають цього.

Числові значення величин, які ми одержуємо в результаті лабораторного експерименту, є наближеними. Навіть значення констант, які ми беремо з таблиць, також наближені. Так, для прискорення вільного падіння ми беремо g = 9,81 м / с², для відношення довжини кола до діаметра π=3,14, для маси електрона m =9,1· 10^-31 кг. Для більш точних обчислень беруть точніші значення:

g = 9,80665 м/с²;

π = 3,1416;

m = 9,106 · 10^-31 кг.

Але і ці значення величин є наближеними або в результаті недостатньої точності вимірювання, або в силу того, що одержані шляхом округлення більш точних значень.

Дуже часто люди, що не мають певного досвіду щодо обчислень, намагаються одержати результат із такою точністю, яка не виправдовується точністю величин, з якими вони проводять обчислення. Це призводить лише до даремних витрат зусиль та часу.

Користування мікрокалькулятором або ПК, коли результат на табло містить від 8 до 16 цифр створює ілюзію великої точності обчислень, але це не так.

2. Похибки. Різниця між точним числом х та його наближеним значенням х_а має назву похибки даного наближеного числа.

Абсолютна похибка ,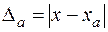

відносна похибка .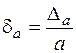

3. Значущі цифри. Наближене число звичайно характеризують кількістю значущих цифр. До значущих цифр відносять всі цифри крім нулів з лівого боку. Так, наприклад, числа 253; 702; 0,00375 мають по три значущі цифри.

Кажуть, що число а має всі знаки вірні, якщо похибка не перевищує половини одиниці розряду останньої цифри наближеного числа. Наближені числа слід записувати так, щоб зберігалися лише вірні знаки.

Якщо число а має n вірних значущих цифр, то його відносна похибка може бути знайдена за формулою:

,

де Z – перша значуща цифра числа а.

4. Округлення. При округленні числа зберігаються лише вірні знаки, зайві знаки відкидаються. Якщо відкидається цифра більша від 5, то попередня цифра збільшується на одиницю. У випадку, коли відкидається цифра 5, округлення виконується так: якщо попередня цифра парна, вона залишається сама собою, якщо непарна – збільшується на одиницю.

Приклади: округлення до трьох значущих цифр:

4,5237» 4,52;

2,3152» 2,32;

Дата добавления: 2014-11-07