Розділ 4. Метод найменших квадратів

Метод найменших квадратів (МНК) використовують як у навчальному процесі, так і в інженерній практиці при обробці результатів за допомогою комп’ютера. Найчастіше студенти не знайомі з основами методу. Тому в даному розділі стисло подано математичну суть МНК, яка полягає в мінімізації суми квадратів відхилень S експериментальних точок 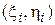від теоретичних даних:

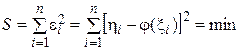. (4.1)

Подавши функцію у вигляді степеневого ряду

,

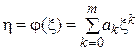на основі (4.1) одержуємо:

.

Завдання полягає у відшуканні таких значень а _k, при яких S мінімальна. Умовою мінімуму є рівність нулю часткових похідних від S по всіх а_k:

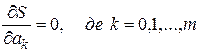. (4.2)

При цьому вираз (4.2) є системою m +1 рівнянь для визначення а_k:

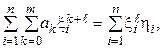де l = 0, 1, …, m; k = 0, 1, …, m. ( 4.3)

Найпростішим є випадок, коли – лінійна функція. До нього зводиться більшість задач лабораторного практикуму, оскільки майже завжди можна вказати такі перетворення величин 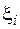і 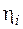, коли залежність між новими масивами змінних , 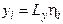стає лінійною:

y = ax + b. (4.4)

Система рівнянь (4.3) для залежності (4.4) має простий вигляд:

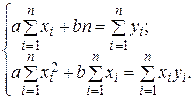(4.5.)

Розв’язуючи (4.5), знаходимо:

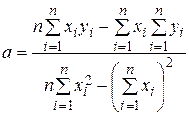, (4.6)

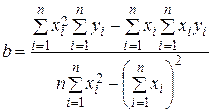. (4.7)

Додатково, на основі теорії кореляцій, для рівняння лінійної регресії вигляду (4.4) встановлюються середньоквадратичні помилки і 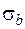визначення коефіцієнтів a і b:

, (4.8)

, (4.9)

а також коефіцієнт лінійного кореляційного зв’язку величин [ x_i ] і [ y_i ]:

. (4.10)

При значенні ρ = 1 існує функціональний зв’язок між x_i і y_i.

Експериментальні дані при цьому точно вкладаються на пряму вигляду (4.4). Розкид величин x_i і y_i, зумовлений помилками експерименту знижує коефіцієнт кореляції. Якщо ρ = 0, величини x_i і y_i повністю незалежні одна від одної.

У деяких випадках залежність 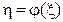не зводиться до лінійної ніякими перетвореннями змінних. Проте, якщо, вона може бути апроксимована степеневим рядом, то застосування МНК за описаною вище методикою хоч і ускладнюється, але все ж залишається принципово можливим. Так, у разі квадратичної залежності

(4.11)

система рівнянь (4.3) відносно a, b, c набирає вигляду:

, (4.12)

Для розв’язання систем (4.5) і (4.12) складені універсальні програми. Перша з цих програм є основною – її можна використовувати при обробці результатів експерименту для більшості задач лабораторного практикуму, друга використовується значно рідше.

Зауваження. Використання цих програм студентом відбувається в комп’ютерному класі в діалоговому режимі і не вимагає від студента додаткових знань з інформатики чи обчислювальної техніки.

Глава ІІ. Лабораторні роботи з основного курсу
фізики

Дата добавления: 2014-11-07