Методика расчета коэффициента Пуассона

Коэффициент Пуассона 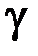численно равен отношению удельных (или молярных) теплоемкостей газа при постоянном давлении и объеме

. (1)

Молярные теплоемкости газа при постоянном давлении 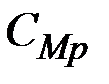и при постоянном объеме определяются соотношениями

и , (2)

где – число степеней свободы молекулы газа.

Следовательно, коэффициент Пуассона 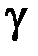зависит от типа молекул газа

. (3)

Коэффициент Пуассона входит в уравнение адиабатного процесса, связывающего, например, давление и объем

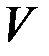
. (4)

Для экспериментального определения коэффициента Пуассона мысленно выделим внутри сосуда произвольную часть воздуха, ограниченную замкнутой поверхностью. Воздух, заключенный внутри этой поверхности, будет расширяться или сжиматься, совершая работу против давления окружающего воздуха в сосуде, и обмениваться с ним теплом. Когда кран соединяет сосуд с атмосферой, давление выделенной массы воздуха равно атмосферному давлению , а ее температура равна комнатной температуре.

Параметры, характеризующие состояние воздуха в выделенном объеме, при протекании указанных ниже процессов (рис. 2) имеют следующие значения:

I состояние (в конце изохорного охлаждения) – , , ;

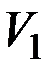II состояние (в конце адиабатного расширения) – , , ;

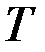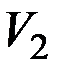III состояние (в конце изохорного нагревания) – , , .

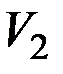При адиабатном переходе воздуха из состояния I в состояние II теплообмена с окружающей средой не происходит

Взяв полный дифференциал от выражения (4), получим после преобразования

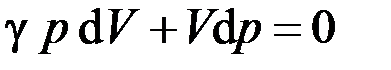. (5)

Разности давлений и много меньше атмосферного давления , поэтому для упрощения расчетов эти разности можно принять за бесконечно малые величины. Последнее относится и к соответствующим изменениям объема выделенной части воздуха. С учетом этого уравнение (5) можно записать в виде:

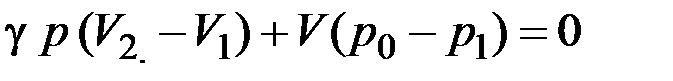. (6)

В состояниях I и III температура газа одинакова, поэтому для этих состояний будет одинаковым и произведение 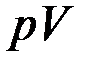, то есть 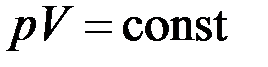и полный дифференциал:

,

или

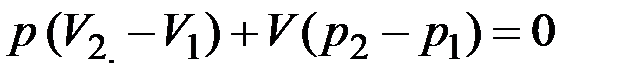. (7)

Из уравнений (6) и (7) выразим коэффициент Пуассона

. (8)

Учитывая, что давление воздуха в конце изохорного охлаждения зависит от атмосферного давления и добавочного давления, определяемого разностью уровней 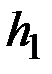жидкости в манометре, получим

, (9)

где ρ – плотность жидкости в манометре.

Давление воздуха в конце изохорного нагревания определяется соотношением

. (10)

Решая совместно уравнения (8)–(10), получим формулу для расчета коэффициента Пуассона:

. (11)

Следовательно, метод Клемана – Дезорма для определения коэффициента Пуассона состоит в измерении разности уровней в манометре 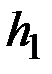(в конце процесса изохорного охлаждения воздуха в баллоне) и 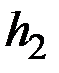(в конце процесса его изохорного нагревания).

Дата добавления: 2014-11-07