Электромагнитные процессы и режимы электрических цепей. Режим синусоидальных токов

Предмет, основные разделы и понятия теоретических основ электротехники

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

Источники энергии

17.1. Гидроэнергетические ресурсы

17.2. Типы гидроэнергетических установок

17.3. Основные схемы использования водной энергии

17.4. Регулирование стока реки водохранилищем

17.5. Гидроэлектростанции и их энергетическое оборудование

17.6. Мощность ГЭС и выработка энергии

17.7. Гидротехнические сооружения ГЭС

17.8. Гидроаккумулирующие электростанции

17.9. Солнечная энергетика

17.10. Ветроэнергетика

17.11. Геотермальная энергетика

Контрольные вопросы

Литература для самостоятельного изучения

Приложение 1

Приложение 2

Словарь основных терминов

Глава первая

Содержание:
1.1.	Предмет, основные разделы и понятия теоретических основ электротехники
1.2.	Электрические цепи: элементы, схемы, законы, классификация
1.3.	Электромагнитные процессы и режимы электрических цепей. Режим синусоидального тока
1.4.	Мощности в цепях синусоидального тока
1.5.	Трехфазные цепи: фазные и линейные токи, напряжения, мощности
1.6.	Электрические цепи несинусоидальных токов
1.7.	Высшие гармоники в трехфазных цепях
1.8.	Мощности в цепях несинусоидальных токов
	Контрольные вопросы
	Литература для самостоятельного изучения

Предметом изучения в дисциплине «Теоретические основы электротехники» (ТОЭ) являются электромагнитные явления и процессы в устройствах и системах электроэнергетики, электротехники и электрофизики. Помимо самостоятельной ценности эта дисциплина призвана обеспечить фундаментальные знания, язык и методологию, необходимые для специальных дисциплин в инженерном образовании электроэнергетиков, электротехников и электрофизиков. Основными разделами ТОЭ являются: «Теория электромагнитного поля» и «Теория электрических цепей», и соответственно важнейшими понятиями являются понятия электромагнитного поля и электрической цепи.

Электромагнитное поле — это особый вид материи (вещества), отличающийся непрерывным распределением в пространстве, обнаруживающий дискретность структуры (кванты излученного электромагнитного поля) и характеризующийся способностью оказывать на заряженные частицы силовое воздействие, зависящее от их скорости. Заметим, что всякая электрически заряженная частица, в том числе элементарная отрицательно заряженная частица — электрон или элементарная положительно заряженная частица — протон, окружена электромагнитным полем, составляющим с ней одно целое. Однако электромагнитное поле может существовать и в свободном состоянии, отдаленном от заряженных частиц, в виде движущихся со скоростью, близкой к 3 · 10⁸ м/с, фотонов или электромагнитных волн. Электромагнитное поле является носителем определенного количества энергии, которая способна преобразовываться в другие виды энергии — механическую, тепловую и т.п. Являясь носителем энергии, поле обладает и определенной массой. Следует заметить, что плотность этой массы в обычных электромагнитных полях весьма невелика. Поэтому на практике этой характеристикой поля обычно не интересуются, сосредоточивая внимание на энергетической стороне рассматриваемых явлений. При изучении электромагнитных явлений принято выделять две стороны — электрическую и магнитную, между которыми существует тесная связь. В соответствии с этим выделяются и две стороны электромагнитного поля — электрическое поле и магнитное поле.

Электрическое поле — это одна из двух сторон электромагнитного поля, обусловленная электрическими зарядами и изменением магнитного поля, оказывающая силовое воздействие на неподвижные заряженные тела и частицы. Для выявления этого поля необходимо рассмотреть неподвижное заряженное тело, поскольку на движущееся тело воздействует не только электрическое, но и магнитное поле. Здесь под зарядом тела понимается совокупный заряд его электрически заряженных частиц. При избытке элементарных заряженных частиц одного знака заряду тела приписывается именно этот знак — отрицательный (при избытке электронов) или положительный (при избытке протонов). Исследуем поле некоторого основного тела с зарядом q. Для этого в различные точки окрестности этого тела будем помещать пробное точечное тело (т.е. тело со столь малыми размерами, что в его пределах исследуемое поле можно считать однородным) с положительным зарядом q ₀. В каждой такой точке на пробное тело будет действовать механическая сила, позволяющая определить основную физическую векторную величину, характеризующую электрическое поле, называемую его напряженностью (рис. 1.1) и равную отношению силы, действующей на точечный электрический заряд в данной точке пространства, к значению этого заряда.*

Таким образом, . Рассмотренный случай электрического поля, обусловленного исключительно неподвижными зарядами, называют также электростатическим полем.

Магнитное поле — одна из двух сторон электромагнитного поля, обусловленная движущимися заряженными частицами и изменением электрического поля, оказывающая силовое воздействие на движущиеся заряженные частицы и выявляемая по силовому воздействию, направленному нормально к направлению движения этих частиц и пропорциональному их скорости.

Для иллюстрации этой стороны электромагнитного поля можно расположить магнитную стрелку вблизи от намагниченных тел или неподвижных проводников с неизменными во времени, т.е. постоянными, токами. В создаваемом этими телами или проводниками соответственно магнитостатическом или стационарном магнитном поле северный конец магнитной стрелки укажет направление основной силовой характеристики магнитного поля — его магнитной индукции (рис. 1.2). Для количественного определения этой физической величины необходимо рассмотреть движущиеся заряды, например, по некоторому проводнику длиной l. Напомним, что движение зарядов называют электрическим током. Пусть 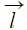— вектор, имеющий длину, равную длине отрезка проводника l, и направленный по оси проводника в направлении тока i, a q — заряд в объеме проводника, движущийся вдоль его оси со скоростью 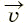. Если заряд q проходит путь l за время t, то , a i = q / t. При этом оказывается, что на проводник с током, расположенный в магнитном поле, действует сила , значение которой пропорционально току i (или заряду q), а направление перпендикулярно оси проводника. Существует определенное направление (обозначим его единичным вектором ), такое, что если ось проводника оказывается перпендикулярной этому направлению, то сила будет максимальной по значению. Именно это направление указала бы магнитная стрелка, будь она расположена на оси проводника. При этом направление будет перпендикулярным как вектору , так и вектору 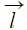(рис. 1.3).

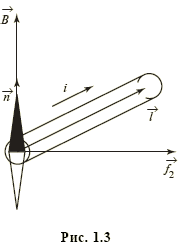
Магнитная индукция — векторная величина, направление которой совпадает с направлением единичного вектора . В общем случае сила определяется из соотношения или , где [,] — знак векторного умножения.

Если направление проводника с током выбрано таким образом, что сила оказывается максимальной по значению (т.е. когда векторы 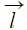, , взаимоперпендикулярны — см. выше), то магнитная индукция находится как 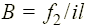или

Выделение из электромагнитного поля двух сторон — электрического поля и магнитного поля оказывается весьма удобным по методическим соображениям. Кроме того, в инженерной практике встречаются ситуации, когда фактически проявляется только одна из этих сторон [как, например, в случае электростатического или магнитостатического поля (см. выше)]. Но в общем случае эти две стороны взаимосвязаны и проявляются совместно. Так, на движущуюся в электрическом поле частицу с зарядом q и скоростью 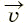действует сила Лоренца , одна из составляющих которой обусловливается электрическим, а другая — магнитным полем.

Познакомимся теперь с рядом понятий — электрическим напряжением, разностью электрических потенциалов и электродвижущей силой, связанных с электрическим полем и необходимых для знакомства с основными понятиями теории электрических цепей.

Пусть частица с зарядом q переносится в электрическом поле из точки А в точку В вдоль некоторого пути (рис. 1.4). Действующие на нее силы совершают работу А, значение которой пропорционально заряду q, а именно А = qU_AB, где величину U_AB называют электрическим напряжением.

Электрическое напряжение — это физическая величина, характеризующая электрическое поле вдоль рассматриваемого пути и равная линейному интегралу напряженности электрического поля вдоль этого пути. В нашем случае (рис. 1.4) . Заметим, что в электростатическом поле интеграл не зависит от выбора пути между точками А и В, т.е. (рис. 1.5).

При этом величину, равную этому интегралу, называют разностью электрических потенциалов точек А и В и обозначают .

В электростатическом поле понятие напряжения между двумя точками тождественно понятию разности потенциалов: U_AB = U_A – U_B. При этом если в поле выбрана некоторая особая точка Р (часто это бесконечно удаленная точка), тогда значение интеграла называют электрическим потенциалом точки А. Если электрическое поле в каждой точке может быть охарактеризовано с точностью до некоторого постоянного значения электрическим потенциалом (как, например, электростатическое поле), то такое поле называют потенциальным полем, в противном случае непотенциальным или вихревым полем. В потенциальных полях линейный интеграл напряженности по любому замкнутому контуру (в частности, контуру AnBmA на рис. 1.5) равен нулю: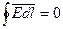(в частности,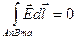). В непотенциальных полях существуют области пространства, в которых. Тогда говорят, что в рассматриваемом контуре действует электродвижущая сила е (сокращенно ЭДС). Источниками таких сил являются, например, электрические генераторы, гальванические элементы, аккумуляторы, термоэлементы и т.п. В этих источниках происходит преобразование энергии какого-либо вида (энергии механического движения, химической, тепловой и т.п.) в электромагнитную, в связи с чем их называют также источниками энергии.

Заметим, что особенности проявления электрических и магнитных полей в веществах, в том числе применяемых в электротехнических, электроэнергетических и электрофизических устройствах, определяемые свойствами этих веществ, позволяют провести классификацию этих веществ. Так, все вещества по их электрическим свойствам могут быть разделены на три основных класса — проводящие вещества (проводники), изолирующие вещества (диэлектрики) и полупроводящие вещества (полупроводники).

Проводящими веществами являются такие, в которых существуют в значительном количестве обладающие зарядом свободные элементарные частицы (электроны или положительные и отрицательные ионы), приходящие в упорядоченное движение под действием электрического поля и образующие тем самым в таком веществе упорядоченный электрический ток. Основным свойством таких веществ является электропроводность, т.е. свойство проводить электрический ток под действием электрического поля. Электрический ток в проводниках называют током проводимости. Проводящими веществами являются металлы, растворы кислот, щелочей, все влажные предметы, как проводник можно рассматривать и человеческое тело.

Диэлектриками называются вещества, в которых свободные частицы, обладающие зарядом, имеются в ничтожном количестве и на первый план выступает явление поляризации. Суть ее заключается в том, что под действием механических сил, обусловленных внешним электрическим полем, частицы молекул, обладающие положительным зарядом, смещаются в сторону поля (в сторону направления вектора ), а частицы, обладающие отрицательным зарядом, смещаются в противоположную сторону. Если напряженность электрического поля не чрезмерно велика, то эти частицы разойтись не могут, так как они удерживаются внутриатомными и внутримолекулярными силами. Считается, что электропроводностью диэлектрики не обладают, но при внесении их в переменное электрическое поле, напряженность которого меняет во времени не только значение, но и направление, вызванное ей движение зарядов в диэлектрике рассматривается как электрический ток, называемый током смещения. К диэлектрикам относятся фарфор, слюда, некоторые масла, сухое дерево. Следует отметить, что идеальных диэлектриков нет, практически все эти вещества в некоторой, но очень незначительной мере обладают свойством электропроводности.

Полупроводящие вещества занимают по значению своей электропроводности промежуточное положение между проводящими веществами и диэлектриками и отличаются рядом специфических свойств, связанных с существованием в них не только электропроводности, обусловленной электронами проводимости, но и электропроводности, обусловленной перемещением под действием электрического поля так называемых «дырок», т.е. незанятых валентными электронами мест в атомах, что эквивалентно перемещению положительных частиц с зарядом, равным по абсолютному значению заряду электрона. Вещества, обладающие подобными свойствами, производятся, например, на основе соединений селена, германия, кремния. Подобные свойства позволяют создавать на основе этих материалов большие группы полупроводниковых приборов, обладающих весьма важными характеристиками, а именно свойствами управления электропроводностью этих приборов. Полупроводниковые приборы — основа современной электроники, находят все большее распространение и в современной электротехнике и электроэнергетике.

Прежде чем перейти к рассмотрению другого важнейшего понятия ТОЭ — электрической цепи, отметим, что использованные выше физические величины принято характеризовать определенными единицами, относящимися к интернациональной системе единиц (СИ), которая содержит семь основных единиц, четыре из которых: метр (1 м) — единица длины; килограмм (1 кг) — единица массы; секунда (1 с) — единица времени; ампер (1 А) — единица силы электрического тока, необходимы для описания всех электромагнитных величин. Другими важными единицами являются: кулон (1 Кл) — единица заряда (1 Кл = 1 А · 1 с), вольт (1 В) — единица напряжения, потенциала, ЭДС; вебер (1 Вб) — единица магнитной индукции.*

Локализацию магнитного поля в ограниченной области пространства, образованного рядом физических устройств, иногда можно описывать более упрощенно, не прибегая к таким понятиям, как магнитная индукция или напряженность электрического поля. В этом случае говорят об электрических цепях. Точнее, совокупность устройств, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении, называют электрической цепью.

1.2. Электрические цепи: элементы, схемы, законы, классификация

Основными элементами электрических цепей являются источники электромагнитной энергии (см. § 1.1), элементы передачи (линии электропередачи, линии связи) и преобразования (трансформаторы, различные преобразователи — выпрямители, инверторы и др.) энергии, а также приемники энергии, в которых электромагнитная энергия преобразуется в энергию других видов, например в механическую (электрические двигатели), химическую (аккумуляторы), тепловую (электрические печи) и т.п.

Источники энергии принято называть активными элементами, а ту часть цепи, в которой они действуют, — активной подцепью, все остальные элементы — пассивными элементами, а часть цепи, в которой нет активных элементов, — пассивной подцепью. Сложность изучения всего многообразия реальных элементов цепей (линий электропередачи, трансформаторов, генераторов и др.) породила необходимость выделения минимального набора простейших элементов, с помощью комбинаций которых можно описывать эти реальные элементы. К таким элементам относят источники энергии: источник ЭДС (схемное обозначение представлено на рис. 1.6, а), источник тока (рис. 1.6, б), резистор (рис. 1.6, в), конденсатор (рис. 1.6, г) и индуктивная катушка (рис. 1.6, д).

Для источника ЭДС (рис. 1.6, а) характерным является равенство напряжения между его выводами значению электродвижущей силы:

(1.1)

для источника тока (рис. 1.6, б) — численное равенство тока i элемента значению тока J источника:

(1.2)

для резистора (рис. 1.6, в) — линейная связь напряжения и тока:

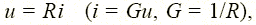
(1.3)

для конденсатора (рис. 1.6, г) — линейная связь тока элемента с производной напряжения:

(1.4)

для катушки (рис. 1.6, д) — линейная связь напряжения с производной тока:

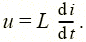
(1.5)

При этом уравнения (1.1)—(1.5) называют компонентными уравнениями рассматриваемых элементов, параметры R (G), С и L этих элементов — соответственно сопротивлением (проводимостью) резистора, емкостью конденсатора и индуктивностью катушки, а значения тока i (t), напряжения u (t) и ЭДС e (t) в момент времени t соответственно мгновенными значениями i, u, e.

Выражение (1.3) носит название закона Ома, а произведение мгновенных значений напряжения и тока p = ui, называемое мгновенной мощностью, для резистора равно р = ui = Ri ² (закон Джоуля—Ленца). Мощность в данном случае определяет количество теплоты, выделяемое резистором в единицу времени. Таким образом, резистор (резистивный элемент) — это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является ом — 1 Ом = 1 В/1 А (проводимости — сименс — 1 См = 1 А/1 В), мгновенной мощности — ватт — 1 Вт = 1 В · 1 А.

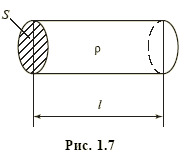
Сопротивлением R можно охарактеризовать любой проводник длиной l и сечением S (рис. 1.7), причем если ток распределен по сечению проводника равномерно, то 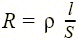, где ρ — удельное электрическое сопротивление, характеризующее свойства материала проводника. Единицей удельного электрического сопротивления является ом х метр (Ом · м). Поэтому в схеме замещения (см. ниже) электрической цепи резистивные элементы отражают не только собственно резисторы, но и сопротивления проводов линий электропередач, сопротивления проводников, из которых выполнены обмотки трансформаторов, электрических машин и т.п.

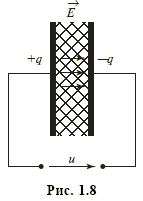
Конденсатор (емкостной элемент) запасает энергию электрического поля W _э = Cu ²/2, его мгновенная мощность 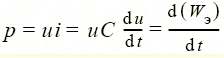— характеризует скорость изменения этой энергии во времени. Конденсатор выполняется в виде двух металлических пластин, разделенных слоем диэлектрика (рис. 1.8). Собственно емкость, для использования которой и предназначен этот элемент, представляет собой отношение двух равных по значению, но противоположных по знаку зарядов пластин, разнесенных в пространстве (рис. 1.8), к напряжению этого элемента С = q / u. Единицей емкости является фарад — 1 Ф = 1 Кл/1 В. Емкостью обладает не только конденсатор, но и пары проводов электропередач, емкостью характеризуется связь каждого из этих проводов с землей и т.д. При составлении схемы замещения реальной цепи необходимо отражать подобные связи емкостными элементами, входящими в схему наравне с конденсаторами.

Катушка индуктивности (индуктивный элемент) запасает энергию магнитного поля W _м = Li ²/2, ее мгновенная мощность 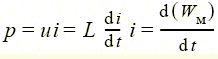характеризует скорость изменения этой энергии во времени. Конструктивно такой элемент часто выполняется из проводника в виде спирали (рис. 1.9).

Ток i в этом случае создает магнитное поле, направление индукции В которого показано линиями со стрелками. Интегрально его можно охарактеризовать для каждого витка потоком через поверхность S. Произведение этого потока на число витков w катушки называют потокосцеплением ψ = Ф w. Индуктивность характеризует связь между этим потокосцеплением и вызывающим его током ψ = Li. Единицей магнитного потока является тесла — 1 Тл = 1 Вб · 1 м², индуктивности — генри — 1 Гн = 1 Тл/1 А. Таким образом, индуктивная катушка — это элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо собственно катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередач, что необходимо отражать в схемах замещения соответствующих цепей.

Таким образом, любая часть реальной электрической цепи обладает всеми перечисленными параметрами — R, L, С, а названные выше — резистор, конденсатор, катушка — суть элементы, в которых соответственно сопротивление, емкость и индуктивность являются основными параметрами, другими же параметрами обычно пренебрегают.

Электрическую цепь удобно изображать в виде чертежа, называемого схемой электрической цепи. Такая схема составляется из условных обозначений элементов цепи (см. рис. 1.6) и показывает их соединение. При этом последовательность элементов, имеющих один и тот же ток, называют ветвью, место соединения ветвей — узлом, замкнутый путь, проходящий по нескольким элементам, называют контуром. Для любого узла справедлив первый закон Кирхгофа: алгебраическая сумма мгновенных значений токов в ветвях, соединенных с данным узлом, равна нулю: ∑ i = 0.

Для любого контура справедлив второй закон Кирхгофа: алгебраическая сумма напряжений на всех элементах любого замкнутого контура равна нулю: ∑ u = 0.

Если число ветвей цепи равно В, узлов У, то число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно У – 1, по второму — В – У + 1. Дополнив В уравнений, составленных по первому и второму законам Кирхгофа (У – 1 + В – У + 1 = В), компонентными уравнениями элементов цепи, можно получить полную систему ее уравнений, позволяющую решить задачу анализа: по заданной схеме и значениям параметров элементов рассчитать неизвестные токи и напряжения ветвей цепи.

Пример 1.1. Для цепи, изображенной на рис. 1.10, имеем: число узлов равно двум, число ветвей — трем, число элементов — четырем. Тогда согласно первому закону Кирхгофа имеем

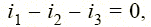
(1.6)

согласно второму закону Кирхгофа:

(1.7)

Компонентные уравнения имеют вид

(1.8)

Полная система уравнений электрической цепи (1.6)—(1.8) позволяет по известным параметрам е = e (t), R, L, С найти все токи и напряжения активного (источник ЭДС) и трех пассивных (резистор, катушка индуктивности, конденсатор) элементов цепи, т.е. решить задачу анализа цепи при условии, что заданы также начальные значения (т.е. значения переменных в момент времени, равный нулю) тока катушки i ₂(0) = i ₀₂ и напряжения конденсатора u ₃(0) = u ₀₃, которые необходимы для решения алгебродифференциальных уравнений (1.6)—(1.8).

В общем случае для решения задачи анализа сложной электрической цепи (т.е. задачи определения всех неизвестных токов и напряжений ее элементов при известной схеме и параметрах — сопротивлениях, емкостях, индуктивностях, ЭДС и токах источников тока) полную систему уравнений составляют редко.

Более эффективными оказываются иные подходы, основанные, например, на различных преобразованиях схем (см. ниже) или использовании более простых — канонических уравнений, связывающих лишь часть из неизвестных переменных. Такие канонические уравнения оказывается возможным составлять относительно переменных, определяющих энергетическое состояние цепи, т.е. запасы ее электрической и магнитной энергии. Поэтому подобные канонические уравнения называют уравнениями состояния электрической цепи, а переменные, относительно которых они составляются, — переменными состояния. Из сказанного следует, что переменными состояния для электрических цепей являются токи индуктивных элементов, определяющих запас магнитной энергии, и напряжения емкостных элементов, определяющих запас электрической энергии.

Пример 1.2. Выразив ток i ₃ из уравнения (1.6) i ₃ = i ₁ – i ₂ и воспользовавшись компонентными уравнениями (1.8) u ₁ = Ri ₁, u = е, из системы уравнений (1.7) найдем

Следовательно,

Тогда из компонентных уравнений (1.8) уравнения u ₂ = u ₃ (1.7) и полученного уравнения для i ₃ находим уравнения состояния электрической цепи, изображенной на рис. 1.10:

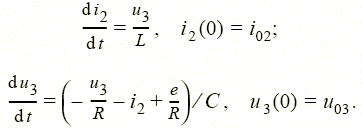
Полученная в примере 1.2 каноническая форма дифференциального уравнения удобна для аналитического либо численного (с помощью стандартных пакетов программ интегрирования дифференциальных уравнений) решения. Под решением здесь понимаются определенные зависимости тока индуктивного элемента i ₂ = i ₂(t) и напряжения емкостного элемента u ₃(t) от времени. Располагая такими зависимостями и уравнениями (1.6), (1.8), аналогичные зависимости от времени для остальных переменных i ₁(t), i ₃(t), u ₁(t), u ₂(t) находят уже с помощью одних алгебраических операций.

Для электрической цепи закон сохранения энергии записывается в виде равенства суммы генерируемых источниками мгновенных мощностей сумме мгновенных мощностей остальных элементов 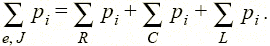Это выражение, представляющее собой запись теоремы Телледжена, показывает, что энергия источников расходуется на теплоту, выделяемую резисторами, и перераспределение запасов электрической и магнитной энергии, запасенных конденсаторами и катушками. В этой связи говорят о балансе мгновенных мощностей цепи.

Пример 1.3. Согласно теореме Телледжена для схемы рис. 1.10 имеем ei ₁ = u ₁ i ₁ + u ₂ i ₂ + u ₃ i ₃, где е = u.

Электрические цепи принято классифицировать по типу параметров элементов и типу электромагнитных процессов в них. Так, говорят о линейных цепях, если параметры элементов е = e (t), J = J (t), R, L, С не зависят от интенсивностей электромагнитных процессов (т.е. от токов и напряжений этих элементов). Подобные цепи описываются линейными системами уравнений, решение которых может быть достигнуто с использованием принципа суперпозиции (наложения), когда можно рассматривать вклад параметра е или J каждого источника энергии в решение независимо от вклада в него других источников. Линейные цепи называют стационарными, если параметры R, L, С их элементов — константы, и параметрическими, если эти параметры известные функции времени R = R (t), L = L (t), С = C (t). Если же параметры е, J, R, L, С зависят от интенсивности процессов, то сами элементы и цепи, их содержащие, называют нелинейными элементами и цепями. Уравнения таких цепей нелинейны, и поиск их решения с гарантированной точностью представляет собой весьма сложную задачу. Различают также элементы и цепи с сосредоточенными и распределенными параметрами. О сосредоточенных параметрах R, L, С говорят в том случае, когда они сосредоточены (локализованы) на определенном участке. Если же приходится учитывать геометрическую протяженность этого участка, то эти параметры считаются распределенными. Параметры R, L, С в этом случае характеризуют единицами Ом/м, Гн/м, Ф/м. Цепи с распределенными параметрами описываются уравнениями в частных производных, решение которых весьма трудоемко. Следует отметить, что допущение о линейности и сосредоточенности параметров справедливо лишь для определенных диапазонов интенсивностей процессов, т.е. является условным, и в этом смысле говорят о границах абстракций в теории электрических цепей. По типу электромагнитных процессов цепи подразделяют на цепи постоянных токов (если токи и напряжения всех элементов цепей не изменяются во времени), цепи переменных токов (если токи и напряжения всех элементов цепей изменяются во времени) и, в частности, цепи синусоидальных токов (если эти токи и напряжения цепей изменяются во времени по синусоидальным законам).

Следует заметить, что в частных случаях, когда процессы в цепях описываются функциями одного вида, например постоянными или синусоидальными функциями, расчет цепей резко упрощается. Существует масса приемов и методов расчета таких цепей. Ознакомимся с некоторыми из них. Но прежде всего обратим внимание на то, что в схемах замещения цепей постоянных токов отсутствуют емкостные и индуктивные элементы. В самом деле, из допущения о постоянстве тока из компонентного уравнения (1.5) индуктивного элемента (см. рис. 1.6, д) следует, что напряжение его будет равным нулю, т.е. сам индуктивный элемент в схеме замещения цепи на постоянном токе представляет собой идеальный проводник с нулевым сопротивлением — так называемую «закоротку». Из допущения о постоянстве напряжения для емкостного элемента (см. рис. 1.6, г) из компонентного уравнения (1.4) следует, что его ток в этом случае будет равен нулю, а сам емкостной элемент представляет собой «разрыв» ветви цепи. Полученная резистивная цепь описывается уже не дифференциальными, а чисто алгебраическими уравнениями, решение которых не представляет особой сложности.

Пример 1.4. Схема рис. 1.10 для случая, когда ЭДС источника e (t), токи i ₁(t), i ₂(t), i ₃(t) и напряжения u ₁(t), u ₂(t), u ₃(t) постоянны, т.е. е = Е, i ₁ = I ₁, i ₂ = I ₂, i ₃ = I ₃, u ₁ = U ₁, u ₂ = U ₂, u ₃ = U ₃, может быть представлена в виде рис. 1.11. При этом I ₃ = 0, U ₂ = 0, а токи I ₁ = I ₂ и напряжение U ₃ находятся из уравнений второго закона Кирхгофа U ₁ + U ₂ = Е, U ₃ = U ₂, где U ₁ = I ₁ R. Окончательно имеем I ₁ = I ₂ = E / R.

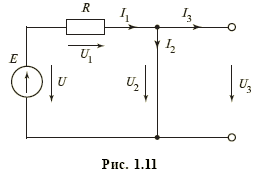
При расчетах резистивных цепей можно пользоваться следующими преобразованиями, основанными на использовании компонентных уравнений и уравнений Кирхгофа:

последовательно соединенные резисторы с сопротивлениями R ₁ и R ₂ (рис. 1.12, а) можно заменить одним эквивалентным резистивным элементом с сопротивлением R _э = R ₁ + R ₂ (рис. 1.12, б), не изменив при этом общего тока I и на пряжения U ветви;

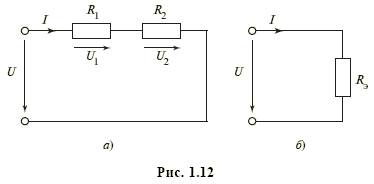
параллельно соединенные резисторы с проводимостями G ₁ = l/ R ₁ и G ₂ = l/ R ₂ (рис. 1.13, а) можно заменить одним эквивалентным резистивным элементом с проводимостью G _э = G ₁ + G ₂ (с сопротивлением 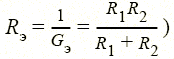(рис. 1.13, 6), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи;

источник ЭДС Е с внутренним сопротивлением R _вн (рис. 1.14, а) можно заменить источником тока J с внутренней проводимостью G _вн (рис. 1.14, б) при условии J = E / R _вн, G _вн = 1/ R _вн; аналогично источник тока J с внутренней проводимостью G _вн (рис. 1.14, б) можно заменить источником ЭДС Е = J / G _вн с внутренним сопротивлением R _вн = 1/ G _вн (рис. 1.14, а), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи.

Используя подобные методы преобразования схемы цепи, можно существенно упростить ее схему и соответственно расчет токов и напряжений. Наряду с подобными методами преобразования при расчете цепей постоянных токов или в более общем случае любых чисто резистивных цепей используют и специальные методы упрощения их схем. Наиболее известным из них является метод эквивалентного генератора.

Суть его сводится к эквивалентной замене любого активного (т.е. содержащего источники энергии) двухполюсника А (т.е. подцепи, присоединенной к остальной части цепи двумя узлами) (рис. 1.15, а) источником ЭДС Е _г, называемой ЭДС эквивалентного генератора с последовательно включенным внутренним сопротивлением R _г (рис. 1.15, 6). При этом значение Е _г равно напряжению так называемого «холостого хода», т.е. напряжению U на разомкнутых зажимах двухполюсника. Это напряжение можно непосредственно измерить, если цепь существует в виде реального устройства, или рассчитать, если она задана в виде схемы с известными параметрами. Внутреннее сопротивление такого генератора определяется как сопротивление двухполюсника А с замкнутыми источниками ЭДС и разорванными ветвями с источниками тока.

Пример 1.5. Определим параметры эквивалентного генератора активного двухполюсника (рис. 1.16, а). «Закоротив» источник ЭДС Е ₁ и «разорвав» ветвь с источником тока J ₂, получим схему рис. 1.16, б, эквивалентное сопротивление которой R ₁ + 1/ G ₂ как раз и будет равно внутреннему сопротивлению эквивалентного генератора, т.е. R _г = R ₁ + 1/ G ₂. Для определения ЭДС этого генератора заменим источник тока J ₂ с проводимостью G ₂ эквивалентной ЭДС Е ₂ = J ₂/ G ₂ с сопротивлением R ₂ = 1/ G ₂ (см. выше). Напряжение холостого хода (I = 0) для полученной схемы (рис. 1.16, в) будет, очевидно, равно U = E ₁ – E ₂. Таким образом схему, изображенную на рис. 1.16, а, можно заменить эквивалентным генератором, изображенным на рис. 1.15, б, с параметрами Е _г = E ₁ – J ₂/ G ₂, R _г = R ₁ + 1/ G ₂. Заменяя отдельные подцепи, соединенные с остальной частью цепи только двумя узлами, подобными эквивалентными генераторами, можно существенно упростить расчет цепи.

В общем случае методика расчета сложной электрической цепи, основанная на замене ее отдельных подцепей более простыми подцепями (типа эквивалентных генераторов для двухполюсников), называется диакоптикой электрических цепей. Введенная в теорию электрических цепей Г. Кроном диакоптика является в настоящее время одной из наиболее востребованных практикой методикой их расчета.

Электромагнитные процессы электрических цепей принято делить на установившиеся, когда токи и напряжения всех элементов цепи описываются периодическими функциями времени (как, например, в цепях постоянного и синусоидального токов), и переходные. Последними называются процессы перехода от одного установившегося состояния к другому. Установившиеся процессы принято называть режимами; так, говорят о режиме постоянного тока и режиме синусоидального тока. В последнем случае токи и напряжения всех элементов имеют вид i = I_m sin(ω t + ψ _i), u = U_m sin(ω t + ψ _u), где ω = 2πf— угловая частота; f = 1/ T — частота процесса (Т — его период), I_m и U_m — амплитуды токов и напряжений, а ψ _i и ω _u — их начальные фазы (рис. 1.17).

Разность фаз φ = ψ _u – ψ _i называется их сдвигом. Из выражений (1.3)—(1.5) следует, что на резисторе фазы напряжения и тока совпадают (φ = 0), на конденсаторе фаза напряжения ψ _u отстает от фазы тока на угол π/2 (φ = –π/2), а на индуктивной катушке ψ _u опережает ψ _i на угол π /2 (φ = π /2). Для оценки интенсивности синусоидальных процессов вводят понятие о действующих значениях токов, напряжений, ЭДС. Для введения этого понятия рассмотрим среднее за период значение мгновенной мощности, характеризующее выделение теплоты в резисторе:

Если учесть, что

,

где . Величину I называют действующим значением синусоидального тока с амплитудой I_m. Численно она равна постоянному току, который вызывал бы в резисторе такие же потери энергии за период времени Т, как и рассматриваемый синусоидальный ток. Действующие значения напряжения U и ЭДС Е также связывают с их амплитудными значениями соотношениям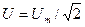и и .

Режим синусоидальных токов играет особую роль в электроэнергетике, поскольку генерация, передача, распределение энергии происходят в основном именно в этом режиме при частоте f = 50 1/с, или 50 Гц (в США — 60 Гц), называемой промышленной частотой. Поэтому методам описания и расчета такого режима обычно уделяют повышенное внимание.

Основным методом расчета электрических цепей синусоидальных токов (расчета синусоидальных режимов) является комплексный или символический метод, предложенный американским инженером Ч. Штейнмецом. Суть его заключается в том, что каждой синусоидальной функции времени (тока, напряжения, ЭДС) сопоставляется комплексное число, а всем действиям с этими функциями — весьма простые действия с комплексными числами. Так, синусоидальным функциям тока i = I_m sin(ω t + ψ _i) и напряжения u = I_m sin(ω t + ψ _u), графики которых изображены на (рис. 1.17), можно сопоставить комплексные амплитуды , или коплексные действующие значения 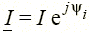, , которые можно изобразить на комплексной плоскости соответствующими векторами (рис. 1.18). Здесь вертикальная ось — ось мнимых чисел, горизонтальная — вещественных чисел. Помимо такой показательной формы записи комплексов I, U, последние можно представить и в алгебраической форме I = Re I + j Im I, U = Re U + j Im U.

Компонентные уравнения (1.3)—(1.5) в комплексном методе приобретают чисто алгебраический вид U = R I, I = j ω C U, U = j ω L I, где j — мнимая единица (иначе, оператор поворота)*. Таким образом, схеме рис. 1.10 в этом методе сопоставляется комплексная схема замещения, изображенная на рис. 1.19. Полная система уравнений такой схемы I ₁ – I ₂ – I ₃ = 0, U ₁ + U ₂ – U = 0, U ₂ = U ₃, U = E, U ₁ = R I, U ₂ = j ω L I ₂, 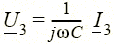, носит чисто алгебраический характер. Заметим, что последние три уравнения выражают закон Ома для резистивного и двух реактивных (индуктивного и емкостного) элементов.

Параметры R, ω L = X_L и 1/ω С = Х_C называют соответственно активным, индуктивным и емкостным сопротивлениями. Решив последние семь уравнений в комплексной области, можно затем от комплексов токов и напряжений всех элементов перейти к соответствующим функциям времени. Комплексным сопротивлением Z (или комплексной проводимостью Y = 1/ Z) можно охарактеризовать и любой пассивный двухполюсник (т.е. часть цепи, подсоединенную к остальной цепи двумя узлами). Так, комплексное сопротивление пассивного двухполюсника, подсоединенного к источнику Е, , где Z ₂ = j ω L, Z ₃ = 1/ j ω C. Зная его, можно сразу же рассчитать входной ток цепи I ₁ = U / Z = E / Z.

Таким образом, комплексный метод расчета позволяет алгебраизовать систему уравнений цепи, а само введение комплексов дает богатые возможности привлечения геометрических построений при суммировании или умножении векторов, соответствующих этим комплексам.

В цепях синусоидального тока особую роль играет понятие резонанса. При резонансе амплитуды тока и напряжения какого-либо участка цепи резко возрастают, а сами ток и напряжение оказываются полностью совпадающими по фазе. Рассмотрим последовательное соединение резистора с сопротивлением R, катушки с индуктивностью L и конденсатора с емкостью С (рис. 1.20, а). Эквивалентное сопротивление этого участка цепи

а его модуль 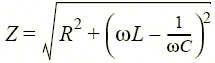будет иметь минимальное значение Z = R при ω L = 1/ω С. При заданном напряжении участка U ток I будет максимален при минимальном Z = R, фаза тока I = U / Z при Z = R будет совпадать с фазой напряжения. Поэтому рассмотренный случай равенства индуктивного ω L и емкостного 1/ω С сопротивлений как раз и определяет условие резонанса. Очевидно, что достичь условия ω L = 1/ω С можно, изменяя любой из трех параметров ω, L, С. В частности, резонанса можно достичь, меняя угловую частоту до значения .

Рассмотрим векторные диаграммы трех случаев соотношений X_L = ω L и X_С = 1/ω С. В первом случае X_L > Х_С и цепь носит активно-индуктивный характер, входное напряжение U опережает по фазе ток I цепи (рис. 1.20, б). Во втором случае X_L < Х_С и цепь носит активно-емкостной характер, напряжение U отстает по фазе от тока I (рис. 1.20, в). В резонансном случае X_L = Х_С, а напряжение на катушке равно по модулю напряжению на конденсаторе и противоположно по фазе: U_L = – U_C, они компенсируются, и со стороны входных узлов цепь может рассматриваться как чисто резистивная (рис. 1.20, г).

В общем случае мы будем рассматривать некоторый пассивный двухполюсник (рис. 1.21, а), состоящий из резисторов, катушек, конденсаторов и находящийся в условиях резонанса, если его входные ток I и напряжение U совпадают по фазе, т.е. его входное сопротивление Z = U / I носит чисто резистивный характер (Z = R). Такой двухполюсник можно заменить резистивным элементом (рис. 1.21, б).

Рассмотрим в качестве еще одного примера резонанс токов, возникающий в цепи, изображенной на рис. 1.22, а, при условии равенства проводимостей катушки 1/ω L, и конденсатора ω С. Токи I _L и I _C в этих элементах будут равны и противоположно направлены, что графически изображено на векторной диаграмме (рис. 1.22, б). При заданном токе I напряжение U цепи (рис. 1.22, а) будет максимальным по модулю и совпадающим по фазе с током при активной проводимости G = 1/ R.

Резонанс на практике играет как положительную, так и отрицательную роль. На основе явления резонанса решается так называемая задача компенсации реактивной мощности (см. следующий параграф), позволяющая достичь наибольшей эффективности передачи электрической энергии в электроустановках и энергосистемах.

Дата добавления: 2014-10-15