Мощности в цепях синусоидального тока

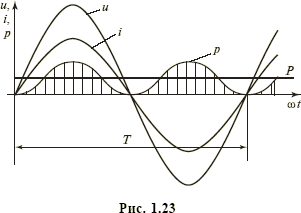
Как было показано выше, мгновенная мощность резистивного (см. рис. 1.6, в) элемента с током i = I _msinω t и напряжением u = RI _msinω t изменяется по закону (рис. 1.23)

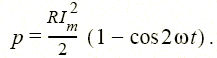
Среднее значение этой мощности

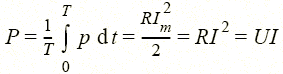
называют активной мощностью.

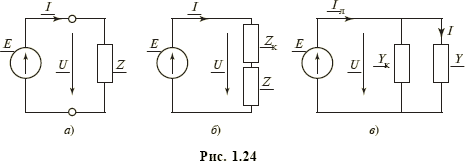
Активная мощность конденсатора и катушки индуктивности равна нулю. Активная мощность пассивного двухполюсника Z (рис. 1.24, а) с сопротивлением Z = Z e ^{j φ} равна Р = UI cosφ, где U и I — действующие значения его напряжения и тока, а φ — угол сдвига между ними.

Наибольшая активная мощность двухполюсника Z (рис. 1.24, а), возможная при данных значениях U и I, называется полной мощностью. Она равна S = UI, а отношение активной мощности Р к полной мощности S, характеризующее его энергетическую эффективность, называется коэффициентом мощности P / S = cosφ. Наряду с активной мощностью для двухполюсника (рис. 1.24, а) вводят понятие реактивной мощности Q = UI sinφ. При этом очевидно, что S ² = Р ² + Q ².

Следует заметить, что в отличие от положительных значений S и Р реактивная мощность может быть как положительной (при активно-индуктивном характере двухполюсника, т.е. при ), так и отрицательной (при активно-емкостном его характере, т.е. при 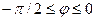). Реактивная мощность резистивного элемента равна нулю (Q = 0 при φ = 0). Единицей полной мощности S является вольт-ампер (1 В · А), единицей активной мощности Р — ватт (1 Вт), реактивной мощности — вар (1 вар). Если напряжение и ток двухполюсника заданы комплексами действующих значений 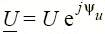, , 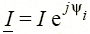то можно ввести комплексную мощность 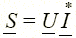, где 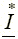— сопряженный комплекс тока 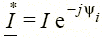. При этом

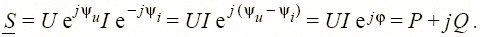
Для комплексных мощностей элементов цепи также справедливо утверждение (теорема Телледжена) о равенстве мощностей, генерируемых источниками (и), и мощностей, потребляемых (п) всеми остальными элементами, т.е. .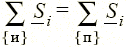

Пример 1.6. Для схемы рис. 1.19 имеем .

Из приведенного баланса комплексных мощностей следует необходимость выполнения баланса для их активных и реактивных составляющих 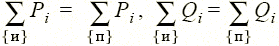(теорема Ланжевена).

В заключение остановимся на проблеме повышения коэффициента мощности (cosφ → 1), или, что то же, снижения реактивной мощности (| Q | → 0) для генераторов, работающих на комплексную нагрузку Z = R + jX (рис. 1.24, а). Включение последовательно с ней компенсирующего реактивную мощность и не потребляющего активной мощности устройства (рис. 1.24, б) с сопротивлением

Z _к = – jX позволяет при тех же токе I и мощности 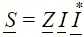нагрузки уменьшить мощность генератора (источника) 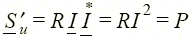, сделав ее чисто активной, и снизить его напряжение Е ' = U ' = I R. Параллельное нагрузке с проводимостью Y = l/ Z = G – jB включение компенсирующего устройства (рис. 1.24, в) с проводимостью Y _к = jB позволяет при тех же мощности S, напряжении U и токе I нагрузки снизить ток в линии и генераторе I _л = GE < I, а также его мощность , которая будет уже чисто активной. Решение проблемы компенсации реактивной мощности повышает эффективность работы соответствующих цепей и позволяет снизить массогабаритные и стоимостные характеристики их элементов. Заметим, что компенсация реактивной мощности по схеме рис. 1.24, б основана на использовании резонанса напряжений, а по схеме рис. 1.24, в — резонанса токов.

1.5. Трехфазные цепи: фазные и линейные токи, напряжения, мощности

Трехфазной электрической цепью называют связную совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе и создаваемые общим источником энергии — трехфазным генератором. Отдельные цепи, входящие в состав такой цепи, называются фазами и обычно обозначаются буквами A, В, С, а совокупность ЭДС, действующих в этих фазах, а также совокупность токов и напряжений фаз называется трехфазной системой ЭДС, токов и напряжений. Трехфазная система ЭДС (токов, напряжений) называется симметричной, если ЭДС (токи, напряжения) всех фаз равны по амплитуде и сдвинуты относительно друг друга по фазе на угол 2π/3, в противном случае трехфазная система называется несимметричной. Уравновешенной называют такую трехфазную цепь, мгновенная мощность элементов которой не зависит от времени, и неуравновешенной — в противном случае. Уравновешенность является важным качеством трехфазной цепи. Так, момент на валу трехфазного генератора остается в таких системах постоянным, а не пульсирует с угловой частотой 2ω, как это имело бы место в однофазном генераторе, мгновенная мощность которого изменяется с частотой 2 ω. Покажем это на примере цепи с симметричной системой ЭДС:

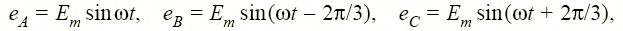
симметричной нагрузкой и, следовательно, симметричной системой токов фаз i_A = I_m sin(φ t – ω), i_B = I_m sin(φ t – 2 π /3 – ω), i_C = I_m sin(φ t + 2 π /3 – ω).

Для мгновенной мощности фаз А, В, С имеем

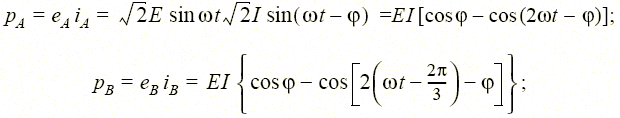
Тогда мгновенная мощность трехфазного генератора p = p_A + p_B + p_C = 3 EI cosφ = Р = const не зависит от времени.

В трехфазных системах применяются два основных способа соединения элементов — соединение треугольником и соединение звездой. На рис. 1.25, а представлена комплексная схема замещения цепи, фазы генератора (А, В, С) и приемника (а, b, с) которой соединены звездой с нейтральным проводом, соединяющим узлы 0 и 0 '; на рис. 1.25, б — схема соединения звездой без нейтрального провода; на рис. 1.25, в представлена комплексная схема замещения цепи, фазы генератора и приемника которой соединены треугольником. В случае симметричности как генератора, так и нагрузки ток I ₀ в нейтральном проводе, соединяющем узлы 0 и 0 ' в цепи рис. 1.25, а, равен нулю: I ₀ = I _A + I _B + I _C = 0. Часто он в таких соединениях отсутствует (рис. 1.25, б), и тогда для соединения генераторов и приемников используется всего три линейных провода с токами I _A, I _B, I _C вместо шести проводов, которые потребовались бы в случае использования трех не связанных между собой однофазных цепей. В этом еще одно достоинство трехфазных систем. При несимметрии токов в фазах по нейтральному проводу протекает ток I ₀, амплитуда которого обычно меньше амплитуды линейных токов I _A, I _B, I _C. Поэтому сечение нейтрального провода выбирается меньшим сечения линейных проводов.

При соединении симметричного генератора треугольником (см. рис. 1.25, в) сумма фазных ЭДС равна нулю, поэтому при отсутствии линейных токов I _A, I _B, I _C (режим «холостого хода») токи в фазах генератора также отсутствуют. Заметим, что и в схеме на рис. 1.25, в для соединения генератора и нагрузки используются только три провода.

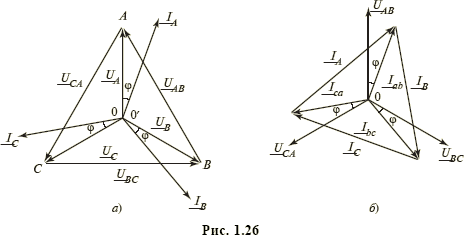
На рис. 1.26, а представлена векторная диаграмма токов и напряжений цепи, изображенной на рис. 1.25, а, в случае симметричности как системы ЭДС, так и нагрузки, а на рис. 1.26, б представлена подобная диаграмма для симметричной цепи рис. 1.25, в. Нагрузка считается активно-индуктивной (т.е.). Из рассмотрения треугольника напряжений (рис. 1.26, а) следует, что линейные напряжения U_AB = U_BC = U_CA = U _л связаны с фазными напряжениями U_A = U_B = U_C = U _ф соотношением . Аналогично рассматривая треугольник токов (рис. 1.26, б), можно записать соотношение для связи линейных I_А = I_В = I_С = I _л и фазных I_АB = I_ВC = I_CA = I_ф токов: 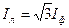. Принимая во внимание, что при соединении ветвей приемника звездой U _ф = U _л /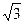, I_ф = I _л, а при соединении их треугольником U _ф = U _л, U _ф = I _л/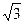, имеем для активной мощности приемника независимо от соединения Р = З U _ф I_ф cosφ = 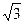, U _л I _лcosφ.

Аналогично для полной и реактивной мощностей симметричного трехфазного приемника

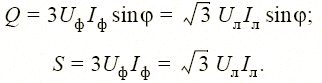
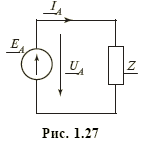
При решении задачи анализа трехфазных цепей общего вида их можно рассматривать просто как сложные электрические цепи, в случае же симметричности систем ЭДС, напряжений, токов для анализа трехфазных цепей достаточно решить задачу для одной фазы, например фазы А. Токи и напряжения других фаз В и С при этом получаются из токов и напряжений фазы А путем фазового сдвига на угол соответственно –2π/3 и +2π/3. Так, симметричной схеме рис. 1.25, а, б можно сопоставить схему рис. 1.27 для фазы А. Очевидно, что ток этой фазы равен

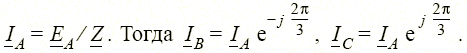
Рассмотренную выше симметричную трехфазную систему ЭДС (напряжений, токов) называют симметричной системой прямой последо­вательности. В ней фазные углы ЭДС (напряжений, токов) уменьшаются на 2л;/3 в порядке следования фаз А, В, С — так как это показано для ЭДС на рис. 1.28, а. Наряду с такой системой в электротехнике используют симметричной системой обратной последовательности, в которой фаз­ные углы ЭДС (напряжений, токов) уменьшаются на 2л/3 в порядке сле­дования фаз А, С, В (см. рис. 1.28, б) и симметричную систему ЭДС (напряжений, токов) нулевой последовательности, в которой фазные углы ЭДС (напряжений, токов) совпадают. Очевидно, что анализ симметрич­ных систем обратной и нулевой последовательностей также может быть сведен к задаче анализа одной фазы, например фазы А.

Для решения задачи анализа трехфазной цепи общего вида, т.е. такой цепи, в которой системы фазных ЭДС (напряжений, токов) не являются

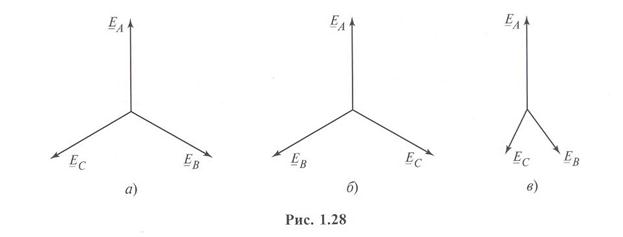
симметричными системами, т.е. амплитуды этих ЭДС (напряжений, токов) не равны по значению и/или углы сдвига ЭДС (напряжений, токов) не одинаково равны 0, 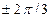(рис. 1.28, в), то такую трехфазную цепь можно рассмотреть просто как сложную цепь. В электротехнике, однако, расчет даже таких цепей сводят к расчету лишь одной их фазы — обычно фазы А. Это оказывается возможным при использовании метода симмет­ричных составляющих (метода Фортескью). Согласно этому методу любую несимметричную систему трехфазных ЭДС (напряжений, токов) представляют в виде суммы трех симметричных трехфазных систем ЭДС (напряжений, токов) соответственно прямой, обратной и нулевой после­довательностей, расчет которых весьма прост и может быть проведен для одной фазы. Таким образом, понятие о симметричных трехфазных систе­мах ЭДС (напряжений, токов) в электротехнике используют для описания процессов даже таких цепей, в которых реально подобные системы таких ЭДС (напряжений, токов) отсутствуют.

Дата добавления: 2014-10-15