Высшие гармоники в трехфазных цепях

В трехфазных цепях гармонический состав токов и напряжений имеет некоторые особенности, которые требуют специального рассмотрения. Пусть фазные ЭДС симметричного трехфазного генератора

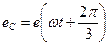— периодические функции с периодом

Т= 2, отличные от синусоидальных. Электродвижущие силы реальных генераторов всегда отличны от синусоидальных функций, но в силу мало­сти этого отличия картину идеализируют, полагая их синусоидальными по форме, что сильно упрощает последующий анализ процессов. Однако в случае, когда необходимо провести более точный анализ или в случае значительной несинусоидальности ЭДС, требуется оценить состав высших гармоник в трехфазных цепях.

В теории трехфазных систем принято выделять три симметричные системы гармонических ЭДС (см. § 1.5). В симметричной системе прямой последовательности фазные углы уменьшаются на 2я/3 в порядке следо­вания фаз А, В, С. В симметричной системе обратной последовательности фазные углы уменьшаются на 2/3 в порядке следования фаз А, С, В. В симметричной системе нулевой последовательности ЭДС совпадают по фазе. В рассматриваемой симметричной системе несинусоидальных ЭДС прямой последовательности функции е_А, е_в, е_с одинаковы по форме и уменьшаются на 2/3 в последовательности фаз А, В, С, где 2— период собственно функции 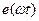и ее первой гармоники. Так как период к-й гар­моники в к раз меньше периода первой гармоники, то угол сдвига к- й гар­моники в последующей фазе по отношению к предыдущей фазе равен к • 2/3. Таким образом несмотря на то, что рассматриваемая система ЭДС и ее первая гармоника образуют прямую последовательность высшие гар­моники ЭДС образуют все три симметричные системы ЭДС.

При этом все гармоники симметричной системы несинусоидальных ЭДС можно разбить на три группы, образующие системы прямой, обрат­ной и нулевой последовательностей (согласно табл. 1.2).

Оценим теперь гармонический состав линейных напряжений обмоток генератора при разных способах их соединения.

Таблица 1.2

Симметричная система	Номера гармоник	Формулы для определения номера к гармоник
Прямой последовательности	1,4,7,10, 13, 16,19,22,25...
Обратной последовательности	2,5,8,11,14, 17,20,23.26...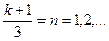
Нулевой последовательности	3,6,9, 12, 15, 18,21,24,27...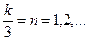

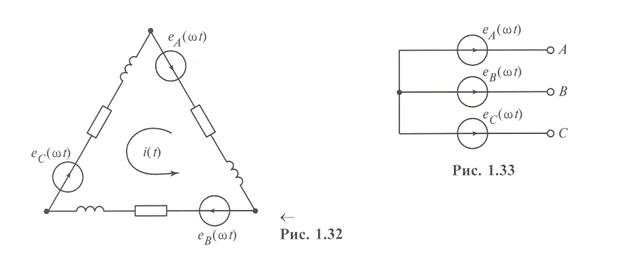
Для всех гармоник как прямой, так и обратной последовательности сумма фазных ЭДС, соединенных треугольником (рис. 1.32) равна нулю и ток в контуре из обмоток генератора не возникает. Ток i(t) вызывается суммарным действием всех гармоник номеров 3п (даже при отсутствии нагрузки генератора), образующих нулевые последовательности фаз. Этот ток вызывает падение напряжения на обмотках фаз генератора, чем ком­пенсирует суммарную ЭДС этих гармоник. Поэтому на внешних выводах обмоток, т.е. в линейных напряжениях этих гармоник (3, 6, 9, 12,...) нет. Заметим, что если генератор устроен симметрично и ЭДС его фаз симмет­рична относительно оси абсцисс [т.е. если ], то в гармо­ническом составе ЭДС нет и четных гармоник (см. § 1.6). Поэтому линей­ное напряжение в этом случае может содержать только гармоники с номерами k = 5, 7, 11, 13, 17, 19, 23, 25,...

При симметрии фазных ЭДС, соединенных в звезду (рис. 1.33), в линейных напряжениях отсутствуют гармоники порядка 3п. Эти гармо­ники присутствуют в фазных напряжениях, но поскольку линейные напряжения равны разности фазных напряжений, то в данном случае она равна нулю, т.к. эти гармоники образуют систему нулевой последователь­ности. Нет в линейных напряжениях и четных гармоник по тем же при­чинам, что и у напряжений генератора, обмотки которого соединены в треугольник (см. выше). Таким образом, в линейных напряжениях могут присутствовать только гармоники с номерами k = 1, 5, 7, 11,... Инте­ресно, что соотношение , справедливое для симметричных систем прямой и обратной последовательностей, здесь нарушается. Дело в том, что гармонический состав линейных и фазных напряжений разный, и если для гармоник номеров, отличных от 3п, это соотношение выдержи­вается, то с учетом сказанного имеем

Несколько слов о влиянии нейтрального провода. В случае его отсутс­твия в линейных токах и токах приемника нет гармоник с номером 3п, т.е.

гармоник, образующих нулевую последовательность фаз, так как их нет в линейных напряжениях. Следовательно, нет этих гармоник и в фазных напряжениях приемника, даже если он соединен звездой. В последнем случае между нейтралью трансформатора и нейтралью генератора появ­ляется напряжение тройной частоты, которое может достигать очень больших значений, опасных для персонала. Наличие нейтрального про­вода избавляет от этой опасности, поскольку для токов нулевой последо­вательности появляется путь нейтральный провод — линейные провода. Заметим, что при наличии обмотки генератора или трансформатора, соединенной треугольником, гармоники порядка 3п удается погасить в обмотках этих треугольников.

Дата добавления: 2014-10-15