Ячеечная модель

Ячеечная модель схематически представляет собой реальный аппарат, как некоторое число n одинаковых последовательно соединенных аппаратов (ячеек) идеального смешения (рис. 6.6).

Рис. 6.6 Ячеечная модель структуры потоков

Суммарный объем всех ячеек равен объему реального аппарата. Следовательно, объем одной ячейки (при условии равенства их объемов):

V_i=.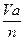

Параметром, характеризующим данную модель, является число ячеек n. Математическое описание ячеечной модели включает n линейных дифференциальных уравнений первого порядка

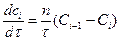i=1,2…n (6.5)

Дифференциальная функция распределения времени пребывания

[кривая отклика С()]: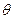

С(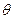) = n^{n 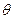n-1} е^-n 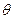/(n-1) (6.6)

График этой функции для различных n представлен на рис. 6.7.

Рис. 6.7. Кривая отклика для ячеечной модели при импульсном вводе индикатора.

При n → ∞ ячеечная модель переходит в МИВ; при n=1 ячеечная модель переходит в МИС, а уравнение (6.6) – в уравнение (6.4). Таким образом, МИВ и МИС являются крайними случаями ячеечной модели.

Из уравнения (6.6) можно вывести простую зависимость для дисперсии ():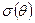

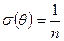(6.7)

Уравнением (6.7) удобно пользоваться для определения числа ячеек.

Дата добавления: 2014-10-15