Аналитические методы

Характеристика методов решения задач оптимизации

При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимальной задачи, а также используемой математической моделью объекта оптимизации.

Группа аналитических методов оптимизации объединяет аналитический поиск экстремума функции, метод множителей Лагранжа, вариационные методы и принцип максимума.

Аналитический поиск экстремума функций, заданных без ограничений на независимые переменные, применяется к задачам, у которых оптимизируемая функция имеет аналитическое выражение, дифференцируемое во всем диапазоне исследования, а число переменных невелико. Это один из наиболее простых методов.

Группа методов математического программирования включает динамическое программирование, линейное программирование и нелинейное программирование.

Динамическое программирование – эффективныйметод решения задач оптимизации многостадийных процессов. Метод предполагает разбивку анализируемого процесса на стадии (во времени или в пространстве) – например, реактор в каскаде или тарелка в колонне. Рассмотрение задачи начинается с последней стадии процесса и оптимальный режим определяется постадийно.

Линейное программирование – метод для решения задач оптимизации с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Подобные задачи решаются итерационными способами. Эти методы используются при оптимальном планировании производства при ограниченном количестве ресурсов, для транспортных задач и др.

Методы нелинейного программирования – объединяют различные способы решения оптимальных задач: градиентные, безградиентные и случайного поиска. Общим для методов нелинейного программирования является то, что их используют при решении задач с нелинейными критериями оптимальности. Все методы нелинейного программирования – это численные методы поискового типа. Суть их – в определении набора независимых переменных, дающих наибольшее приращение оптимизируемой функции. Данная группа методов применяется как для детерминированных, так и стохастических процессов.

Аналитические методы основаны на классических методах математического анализа.

Задача оптимизации формулируется следующим образом. Существует процесс, известна его математическая модель и установлен критерий оптимизации R в виде функции:

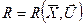(7.3)

Либо функционала:

(7.4), где:

Заданы ограничения: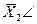

Необходимо при заданных ограничениях найти такие значения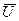, при которых R достигает экстремума. В случае функционала К необходимо найти вид функции , при которой R достигает экстремума.

Аналитические методы поиска экстремума критерия оптимальности применяются к задачам, у которых оптимизируемая функция имеет аналитическое выражение, а число переменных невелико.

В качестве примера рассмотрим определение оптимального времени пребывания смеси в РИВ.

W₁ W₂

Для двух последовательных реакций А -----> В------>D необходимо определить оптимальное время пребывания t_опт, при котором выход целевого продукта В будет достигать максимума.

Пусть а – начальная концентрация компонента А. В начальный момент времени концентрации компонентов В и D равны нулю:

при t=0: C_В = С_D=0;

Критерий оптимизации: выход целевого продукта R=C_B/a. Управляющее воздействие – время пребывания t.

Характер изменения концентраций компонентов во времени приведен на рис. 7.2.

Пусть обе реакции протекают по первому порядку.

Рис. 7.2

W(1)=R(1)*WC(A) (7.5)

W(2)=K(2)*WC(B) (7.6)

dc(b)/dt=W1-W2 (7.7)

Из (7.5) найдем выражение для текущей концентрации С_А.

Преобразуем (7.5):

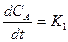-С_А; dt

Проинтегрировав, получим:

In 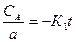(7.8)

Подставим (7.8) и (7.6) в (7.7):

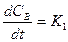ae^-K₁^t –K₂C_B

Или

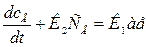
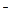
₁ (7.9)

Решив полученное уравнение, найдем выражение для определения текущей концентрации компонента В:

С_B=a 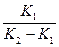(e^-K₁^t - e^-K₂^t)(7.10)

Выход целевого продукта:

R=C_B/a = (e^-K₁^t-e^-K₂^t)(7.11)

Исследуем экстремум полученной целевой функции (7.11). Условия существования максимума dR/dt=0; d²R/dt²<0; Найдем первую производную и приравняем ее нулю:

(-K₁e^-K₁^t-K₂e^-K₂^t) = 0 (7.12)

Решив полученное уравнение, определим оптимальное время пребывания:

t_opt= 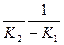In (7.13)

Для проверки выполнения достаточного условия существования максимума вычисляем вторую производную:

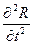= (K₁²e^-K₁^t-K²₂e^-K₂^t)<0

Так как вторая производная меньше 0, то в данной точке существует максимум целевой функции R. Подставив (7.13) в (7.10), получим выражение для определения максимальной концентрации компонента В:

C_{B opt}= a²(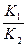) (7.14)

Дата добавления: 2014-10-15