Диффузионная модель

Основой этой модели является модель идеального вытеснения, осложненная обратным перемешиванием, наличие которого описывается формальным законом диффузии:

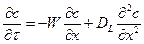(6.8)

т.е. к уравнению (6.2) добавляется диффузионный член, учитывающий турбулентную диффузию или перемешивание (D_L – коэффициент продольной диффузии, учитывающий и молекулярную и турбулентную диффузию, а также неравномерность поля скоростей). В практических задачах D_L обычно является эмпирическим параметром. Причем считается, что D_L постоянен по длине аппарата.

Таким образом, единственным параметром этой модели является коэффициент продольной диффузии D_L (или коэффициент продольного перемешивания). Но при одном и том же значении D_L картина перемешивания может быть разной – на неё влияют также длина аппарата и скорость потока. Поэтому, чтобы распространить результаты на ряд подобных процессов, продольное перемешивание характеризуют критерием подобия Пекле

Pe_L = W L/D_L (6.9)

Анализ уравнения (6.9) показывает, что при Pe = 0 (D_L=∞) поток соответствует идеальному смешению (бесконечно быстрая диффузия полностью выравнивает концентрации). При Pe_L=∞ уравнение (6.8) переходит в уравнение (6.2) – поток движется по схеме идеального вытеснения. Реальному же потоку соответствуют условия 0<Pe<∞

Кривые отклика диффузионной модели при ступенчатом и импульсном возмущении показаны на рис. 6.8.

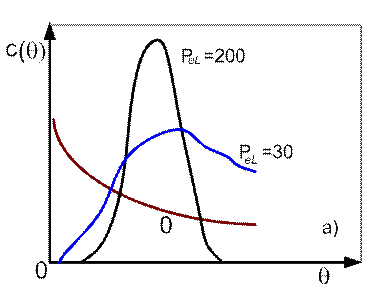
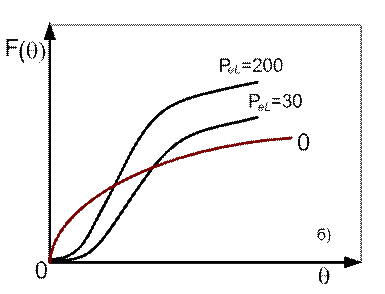
Рис. 6.8. Кривые отклика для диффузионной модели при импульсном (а) и ступенчатом (б) вводе индикатора.

Дисперсию времени пребывания можно рассчитать по формуле:

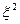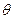() = 2/ Pe_L-2(1-е ^-PeL )/ Pe_L² (6.9)

При Pe_L>10, т.е. когда реальный поток незначительно отклоняется от идеального вытеснения, справедлива приближенная формула:

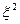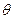() = 2/ Pe_L (6.10)

С учетом (6.7) получим соотношение:

Pe_L / 2 ≈ n (6.11), устанавливающее соответствие между ячеечной и диффузионной моделями.

Диффузионную модель обычно используют для описания структуры потоков в аппаратах с непрерывным контактом фаз (например, в насадочных и пленочных массообменных колоннах и т.п.).

В табл. 6.1 представлены схемы потоков, соответствующие рассмотренным моделям, их математическое описание и кривые отклика.

Таблица 6.1. Схемы потоков, математическое описание их моделей и кривые отклика.

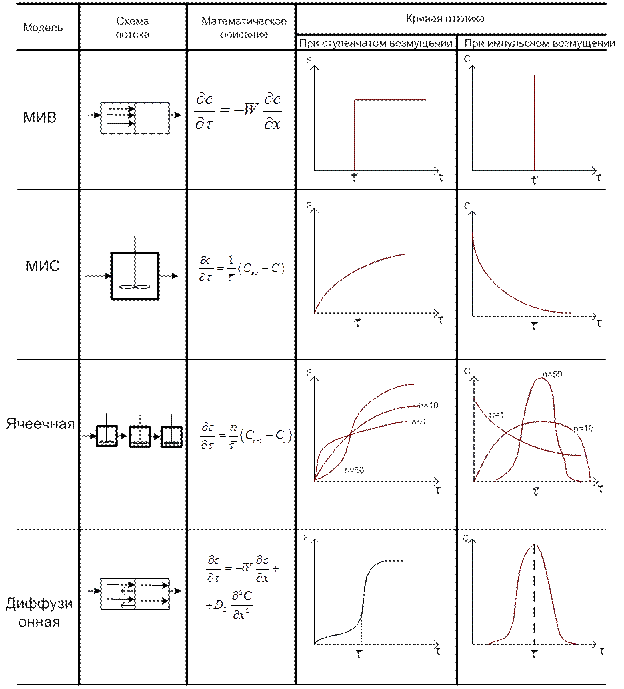
Кроме однопараметрической диффузионной модели достаточно широко используют двухпараметрическую диффузионную модель, учитывающую перемешивание как в продольном, так и в поперечном направлениях. Эта модель характеризуется коэффициентами продольного (D_L) и радиального (D_R) перемешивания:

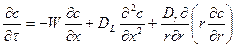(6.12)

где: r- радиус; коэффициенты D_r и D_L определяют опытным путем.

Дата добавления: 2014-10-15