Випадкових величин

Числові характеристики дискретних

Характеристикою середнього значення випадкової величини служить математичне сподівання.

Математичним сподіванням дискретної випадкової величини називають суму добутків всіх її можливих значень на відповідні ймовірності:

Якщо дискретна випадкова величина набуває нескінченну але зчисленну множину можливих значень, причому математичне сподівання існує, то ряд у правій частині рівності збігається абсолютно.

87. Знайти математичне сподівання дискретної випадкової величини X, заданої законом розподілу:

а) X -4 6 10. р 0,2 0.3 0,5

б) X 0,21 0,54 0,61. р 0,1 0,5 0,4

Розв’язання а) Математичне сподівання дорівнює сумі добутків усіх можливих значень X на їх ймовірності:

М(Х) = -4 · 0.2 +6 · 0.3 +10 · 0.5 = 6.

88. Знайти математичне сподівання випадкової величини Z, якщо відомі математичні сподівання X і Y: а) Z =Х +2У, М(Х)=5, М(У) = 3; б) Z=3X 4Y,

M(Х)=2,М(У)=6.

89. Дискретна випадкова величина X набуває три можливих значення: x₁ - 4 з імовірністю p₁ = 0,5; х₂ = 6 з імовірністю p₂ = 0,3 і х3 з ймовірністю p₂. Знайти х₂ і р₂ знаючи, що М (Х) = 8.

90. Даний перелік можливих значень дискретної випадкової величини X: х₁ = 1, x₂ = 2, x₃ =3, а також відомі математичні сподівання цієї величини та її квадрата: M (Х) = 2,3, M (X²) = 5,9. Знайти ймовірності, що відповідають можливим значенням X.

91. Знайти математичне сподівання дискретної випадкової величини X - числа таких підкидань п’яти гральних кісток, в кожному з яких на двох кістках з’явиться по одному очку, якщо загальне число підкидань рівне двадцяти.

Розв’язання. Скористаємося формулою M(Х) = np, де n - загальне число випробувань (кидання п’яти кісток); X - число появ події, що цікавить нас (на двох кістках із п’яти з’явиться по одному очку) в n випробуваннях;

Р - ймовірність появи розглянутої події в одному випробуванні.

За умовою, n = 20. Залишається знайти P - ймовірність того, що на гранях двох із п’яти кісток з’явиться по одному очку. Цю ймовірність обчислимо за формулою Бернуллі, враховуючи, що ймовірність появи одного очка на грані однієї кістки р = 1 / 6 і, отже, ймовірність не появи q = 1-1/6 = 5 / 6:

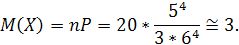
92. Випадкові величини X і Y незалежні. Знайти дисперсію випадкової величини

Z =2 Х+ ЗУ, якщо відомо, що D (X) = 4, D (Y) = 5.

93. Знайти дисперсію дискретної випадкової величини X -числа появ події А в п’яти незалежних випробуваннях, якщо ймовірність появи подій А в кожному випробуванні дорівнює 0,2.

Розв’язання. Дисперсія числа появ події в незалежних випробуваннях (з однаковою ймовірністю появи події в кожному випробуванні) дорівнює добутку числа випробувань на ймовірності появи і непояви події:

За умовою, n = 5; р = 0,2; q = 1 - 0,2 = 0,8. Шукана дисперсія

D (X) = npq.

D (Х) = npq = 5·0,2·0,8 = 0,8.

94. Знайти дисперсію дискретної випадкової величини Х -числа відмов елемента деякого пристрою в десяти незалежних дослідах, якщо ймовірність відмови елемента в кожному досліді дорівнює 0,9.

95. Проводяться незалежні випробування з однаковою ймовірністю появи події А в кожному випробуванні. Знайти ймовірність появи події А, якщо дисперсія числа появ події в трьох незалежних випробуваннях дорівнює 0,63.

96. Дискретна випадкова величина X набуває тільки двох можливих значень: x₁ і x₂, причому х₁ < х₂. Ймовірність того, що X набуде значення x ₂, дорівнює 0,2. Знайти закон розподілу X, якщо математичне сподівання M (X) = 2.6 і середнє квадратичне відхилення σ(X) = 0.8

97. Дискретна випадкова величина X набуває тільки трьох можливих значень: x₁ = 1, х₂ і x₃ причому x₁ <x₂<x₃. Ймовірність того, що X набуде значення x₁ і x ₂ відповідно рівні 0,3 и 0,2. Знайти закон розподілення величини X, якщо її математичне сподівання M(Х) = 2,2 і дисперсія D(X)= 0.76

Дата добавления: 2014-10-15