Прогнозування значень з викорстанням стандартних функцій

Стандартні функції MS Excel можуть використовуватися для прогнозування даних.

Функція ПРЕДСКАЗ обчислює майбутнє значення по існуючим значенням з використанням лінійної регресії. Значення, що прогнозується, є y-значенням, що відповідає заданому x-значенню. Цією функцією можна скористатися для прогнозування майбутніх продажів, потреб в обладнані або тенденцій споживання (рис. 3.25-3.26).

№	Період	Кількість туристів
	1 квартал 2009
	2 квартал 2009
	3 квартал 2009
	4 квартал 2009
	1 квартал 2010
	2 квартал 2010
	3 квартал 2010
	4 квартал 2010
	1 квартал 2011

Рисунок 3.25 – Вхідні дані задачі прогнозування

Структура функції ПРЕДСКАЗ така:

= ПРЕДСКАЗ(Х, Відомі_значення_Y, Відомі_значення_Х) (3.1)

де Х – значення, для якого робиться прогнозування;

Відомі_значення_Y – незалежний масив даних;

Відомі_значення_Х – незалежний масив даних.

Розрахунок значення на наступний період (прогноз)
	2 квартал 2011	=-0,2601*B15^3+3,8582*B15^2-5,2388*B15+33,095	=106

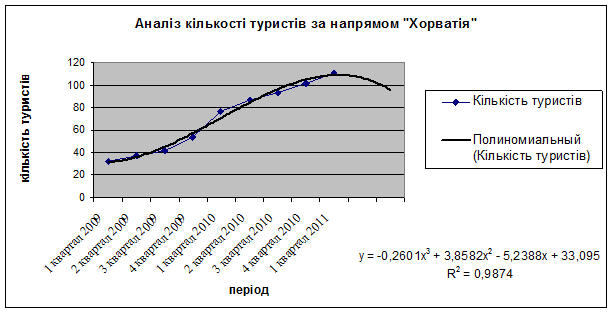
Рисунок 3.26 – Визначення тенденцій за допомогою лінії тренду

Функції ТЕНДЕНЦИЯ і РОСТ дозволяють екстраполювати y-значення, продовжують пряму лінію або експоненційну криву, що найкращим чином описують існуючі дані. Ці функції повертають y-значення, що відповідає заданим x-значенням. Структура функцій така:

= РОСТ() (3.2)

де Х – значення, для якого робиться прогнозування;

Відомі_значення_Y – незалежний масив даних;

Відомі_значення_Х – незалежний масив даних.

=ТЕНДЕНЦИЯ(Відомі_значення_Y, Відомі_значення_Х, Х) (3.3)

де Х – значення, для якого робиться прогнозування;

Відомі_значення_Y – незалежний масив даних;

Відомі_значення_Х – незалежний масив даних.

Функції ЛИНЕЙН і ЛГРФПРИБЛ дозволяють обчислити пряму лінію або експоненційну криву для існуючих даних. Ці функції повертають дані регресійного аналізу, включаючи нахил та зміщення графіку відносно осі Y.

Функція ЛИНЕЙН використовується для розрахунку коефіцієнтів прямої, яка найкращим чином апроксимує вихідні дані і має вигляд: y = mx + b. Діалогове вікно заповнюється за зразком (рис. 3.27).

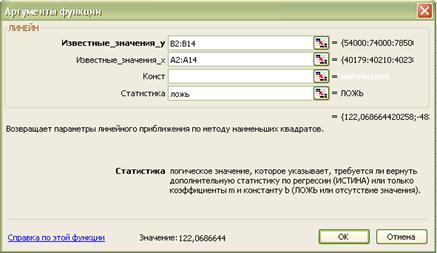
Рисунок 3.27 – Майстер функції ЛИНЕЙН

Після заповнення потрібно натиснути одночасно клавіші Ctrl+Shift+Enter. На основі отриманих коефіцієнтів можна побудувати рівняння прямої:

y=122,07x - 4837596,73 (3.4)

Функція ЛГРФПРИБЛ використовується для розрахунку коефіцієнтів експоненціальної кривої, що апроксимує дані і має вигляд y = b*m^x. Діалогове вікно заповнюється за зразком:

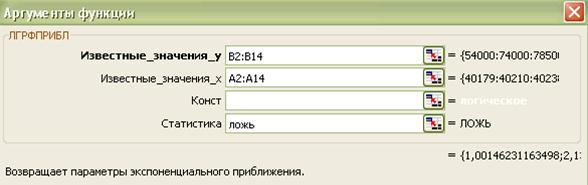
Рисунок 3.28 – Майстер функції ЛГРФПРИБЛ

Після заповнення натиснути одночасно клавіші Ctrl+Shift+Enter. На основі отриманих коефіцієнтів побудувати рівняння експоненціальної кривої.

При необхідності виконання більш складного регресійного аналізу — включаючи обчислення і відображення залишків — можна використовувати засіб регресійного аналізу в надстройці «Пакет анализа».

Наступним етапом розглянемо алгоритм побудови прогнозної моделі для товарів з сезонним характером продажів. Поняття “сезон” в прогнозуванні застосовується до будь-яких систематичним коливань, наприклад, якщо мова йде про вивчення товарообігу протягом тижня під терміном “сезон” розуміється один день. Крім того, цикл коливань може суттєво відрізнятися (як у більший, так і в менший бік) від величини один рік. І якщо вдається виявити величину циклу цих коливань, то такий часовий ряд можна використовувати для прогнозування даних.

У якості початкової інформації для прогнозування була використана інформація про реалізацію туристичних путівок одним з агенств м. Донецька за два сезони F₁, F₂. Дана статистика характеризується тим, що значення обсягу продажів мають виражений сезонний характер із зростаючим трендом.

Для прогнозування обсягу продажів, що має сезонний характер, пропонується такий алгоритм побудови прогнозної моделі [12]:

1. Визначається тренд (Т), що найкращим чином апроксимує фактичні дані. Використання поліноміального тренду при цьому дозволяє суттєво скоротити помилку прогнозної моделі.

y=a₁*xⁿ+a₂*x^n-1+…a₆*x+a₀ - поліноміальна

y= a₁*x+a₀ - лінійна (3.5)

y=a*lnx+b - логарифмічна

2. Визначення величини сезонної компоненти. Вибираючи лінію тренда, що характеризує загальну тенденцію розвитку того явища, що вивчається, необхідно також розрахувати сезонну компоненту (S) і проаналізувати на скільки сильно сума середніх значень S відхиляється від 0. Якщо ця величина близька до 0, то можна стверджувати, що продажі дійсно мають сезонний характер, отже, товар можна назвати сезонним.

S_t,j=F_t,j-T_t,j, j=1,2*n, t=1,2 - сезонна компонента; (3.6)

Avg_i=(S_t,1+S_t+1,2)/2, i=1,n - середнє; (3.7)

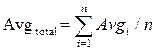, i=1,n - середнє за середнім значенням; (3.8)

S`=Avg_i-Avg_total - скоригована сезонна компонента. (3.9)

Якщо встановлено, що в моделі існує сезонність , то період сезонності розраховується як середня арифметична між кількістю від’ємних та позитивних значень сезонної компоненти.

3. Розрахунок помилки моделі як різниці між фактичними значеннями і значеннями моделі:

E_t,j=F _t,j-(T_t,j+S_j), i=1,n, t=1,2 (3.10)

Замість значень F підставляються фактичні значення обсягів продажів. (T_t,j+S_j) – значення моделі (значення тренду + значення сезонної компоненти).

Адекватність економіко-математичної моделі реальній економічній ситуації можна оцінити за допомогою використання середньої відносної помилки прогнозу:

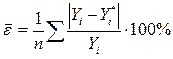, (3.11)

де Y_i – фактичне значення реалізації туристичних путівок;

Y _i ^* - прогнозне значення моделі.

n – кількість спостережень.

Визначається точність моделі: .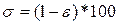

Якщо точність моделі коливається у межах 90%-100%, то можна стверджувати, що модель є достатньо точною.

4. Визначивши найбільш точну модель, можна побудувати прогноз змін продажів.

5. На основі моделі будується остаточний прогноз обсягу продажів:

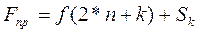(3.12)

де f – функція лінії тренду.

Таким чином, на основі вхідних даних (рис. 3.29) побудуємо прогнозну модель обсягу продажів туристичних путівок, що мають сезонний характер на 12 періодів.

Визначимо тренд, що найкращим чином апроксимує фактичні дані. Для побудови тренду необхідно клацнути правою кнопкою миші по графіку в вибрати команду Добавить линию тренда. У діалоговому вікні вибрати тип лінії тренда найбільш відповідної для даного графіку. Для простоти і більшої наочності даного прикладу, а також віддзеркалення суті запропонованого алгоритму обмежимося вибором трьох ліній тренду: поліноміальний, лінійний та логарифмічний. У результаті виконаної роботи отримаємо графік, зображений на рис. 3.30.

За коефіцієнтами детермінації видно, що найбільш переважний поліноміальний, а найменш — лінійний тренд. Але оскільки коефіцієнт детермінації (R²) не визначає точність всієї моделі, то вибір тренду на цьому етапі ми зробити не можемо.

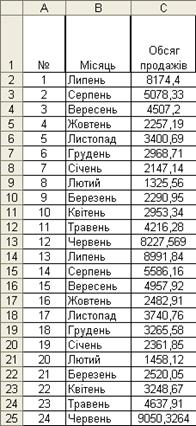
Рисунок 3.29 - Обсяги продажів туристичних путівок у 2010-2011 рр.

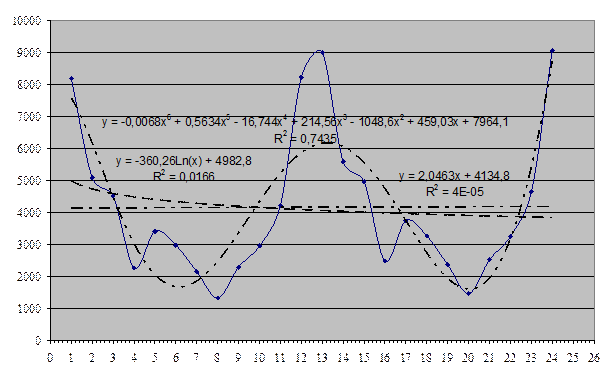
Рисунок 3.30 – Обрані лінії тренду

З урахуванням отриманих рівнянь ліній тренду розрахуємо значення трендів в клітинках D2:F2 підставляючи замість х значення номера періоду (рис. 3.31).

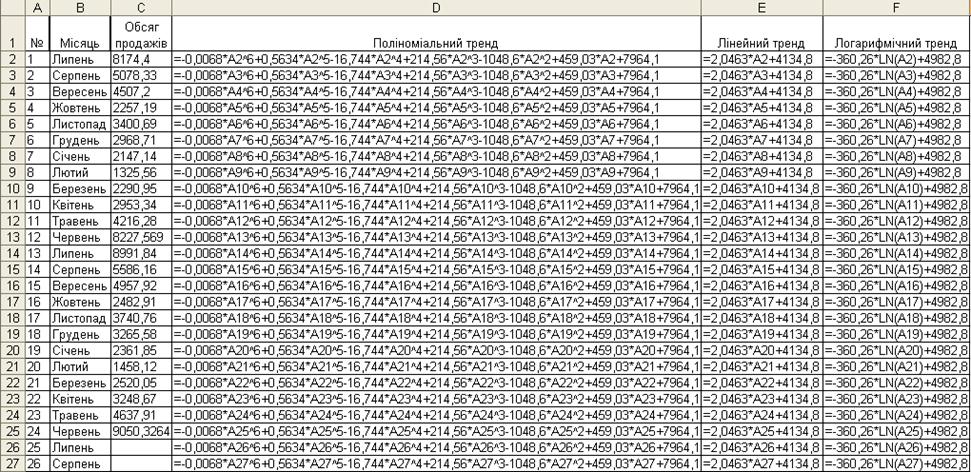
Рисунок 3.31 – Рівняння ліній тренду в режимі формул

Для розрахунку сезонних компонент у клітинках G2:I25 введемо формули різниці обсягу продажів та значень трендів (рис. 3.32).

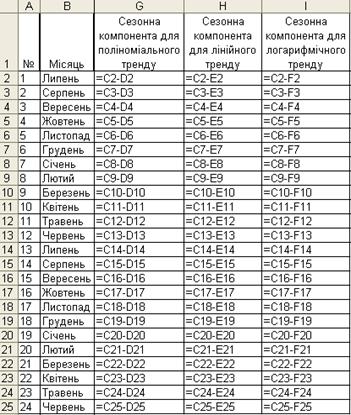
Рисунок 3.32 – Розрахунок сезонних компонент для різних ліній тренду.

У клітинках G2:G13 розрахуємо середнє значення сезонної компоненти відповідних періодів, а також скориговане значення сезонної компоненти за допомогою формул, що надані на рисунку 3.33.

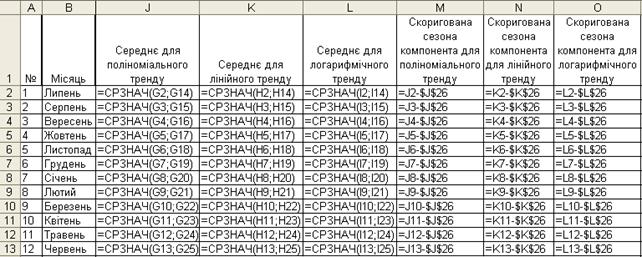
Рисунок 3.33 – Розрахунок середнього значення сезонної компоненти та скоригованого значення сезонної компоненти для трьох трендових моделей

Отримавши три сезонних компоненты (S) з трьома рівняннями тренду (T), можливо розрахувати помилки побудованих моделей (E) за формулою (3.10). Для цього з вихідних фактичних значень необхідно відняти суму S+T. Дані розрахунку представлені на рис. 3.34.

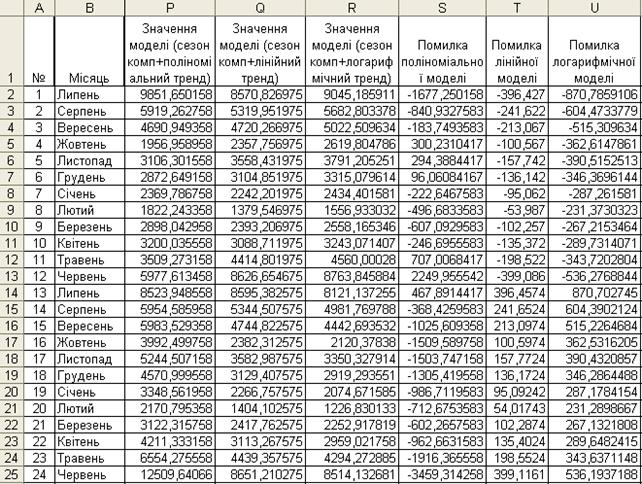
Рисунок 3.34- Значення моделей (T+S) і їх помилок (E)

У клітинці P2 розрахуємо значення отриманої моделі за формулою =D2+M2 і в клітинці S2 помилки моделі як різниця між фактичними значеннями та значеннями моделі (C2-P2). Аналогічно розраховуємо значення та помилки лінейної та логарифмічної моделей. У клітинках V2, W2 та Х2 розрахуємо середньоквадратичні відхилення моделей та середні значення цих показників як показано на рис. 3.35.

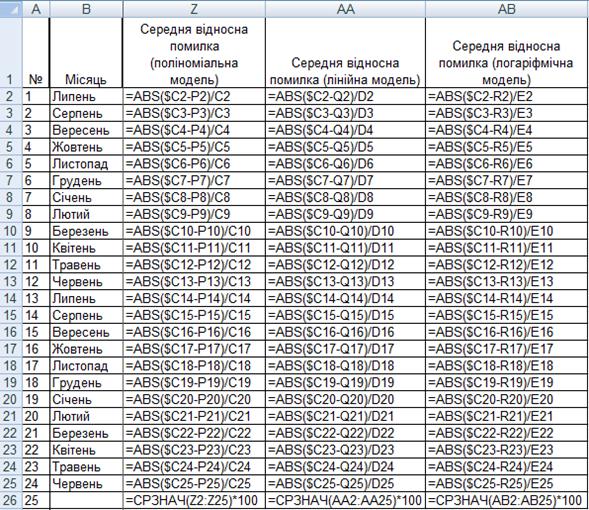
Рисунок 3.35 – Розрахунок середньоквадратичних відхилень моделей

На основі отриманих відхилень визначимо точність моделей за формулою .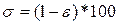

Якщо точність моделі коливається у діапазоні 90%-100%, то можна стверджувати, що модель достатньо точна. В нашому прикладі

точність моделі з поліноміальним трендом = 75,4%

точность моделі з лінійним трендом = 95,96%

точность моделі з логарифмічним трендом = 89,89%

Таким чином, високу точністю мають останні дві моделі (див. рис. 3.36). Проте, модель з лінійним трендом є найбільш точною, оскільки її показник точності найбільш високий. Отже, прогноз, зроблений на підставі даних лінійної моделі буде найбільш точним.

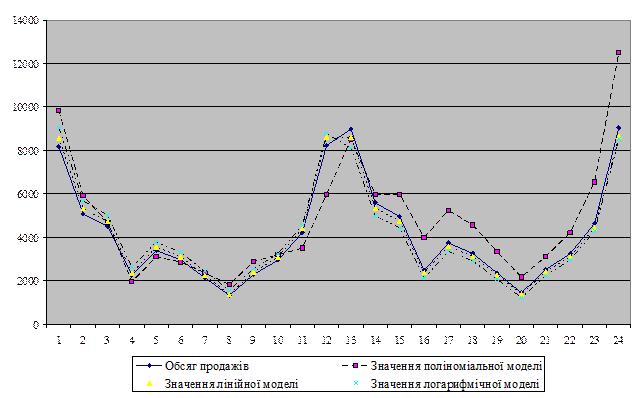
Рисунок 3.36 - Моделі, побудовані на підставі різних ліній тренду

Визначивши найбільш точну модель, можемо побудувати прогноз змін продажів туристичних путівок на наступний сезон. Трендова компонента (Т) залежить від послідовності чисел від 1 до 24. Отже, для побудуви прогнозу, необхідно продовжити цю послідовність до 36. Значення трендової компоненти MS Excel розрахує в автоматичному режимі. Достатньо виділити останню клітинку 24-го місяця і затиснувши чорний квадратик в нижньому правому кутку клітинки протягнути виділення до 36 періоду. У результаті отримаємо трендовую компоненту Т. Сезонна компонента (S) розрахована для моделі, залишається незмінною для 25-36 місяців. Виділимо в MS Excel сезонну компоненту і скопіюємо на періоди 25-36. Для врахування помилок скористаємося довірчим інтервалом моделі, розрахованим для прогнозних значень. Довірчий інтервал відображає, в яких межах може варіюватися прогнозне значення (табл. 3.2).

Таблиця 3.2. - Розрахунок прогнозних значень моделі з лінійним трендом (ймовірність 0,96)
№	Місяць	Лінейний тренд	Скоригована сезона компонента для лінійного тренду	Прогнозні значення лінійної моделі
	Липень	4185,9575	4433,9959	8619,953
	Серпень	4188,0038	1181,0746	5369,078
	Вересень	4190,0501	579,3433	4769,393
	Жовтень	4192,0964	-1785,213	2406,883
	Листопад	4194,1427	-586,5843	3607,558
	Грудень	4196,189	-1042,2106	3153,978
	Січень	4198,2353	-1906,9069	2291,328
	Лютий	4200,2816	-2771,6082	1428,673
	Березень	4202,3279	-1759,9945	2442,333
	Квітень	4204,3742	-1066,5358	3137,838
	Травень	4206,4205	257,5079	4463,928
	Червень	4208,4668	4467,3143	8675,781

Якщо представити графічно прогноз, розрахований за допомогою вибраної моделі то в результаті отримуємо графік, зображений на рисунку 3.37.

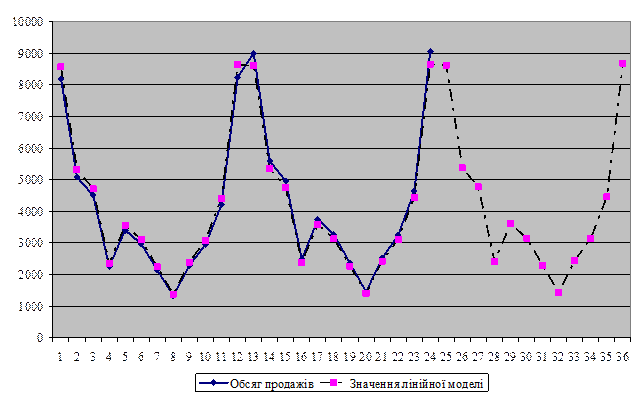
Рисунок 3.37 – Графік з прогнозом значень на наступні два періоди

3.5 Вирішення оптимізаційних задач туристичного бізнесу засобами Microsoft Excel

На практиці постійно зустрічаються такі ситуації, коли досягти якогось результату можна не одним, а багатьма різними способами. Успішність вирішення переважної більшості економічних завдань залежить від найкращого, найвигіднішого способу використання ресурсів. І від того, як будуть розподілені ці, як правило, обмежені ресурси, залежатиме кінцевий результат діяльності туристичної фірми. Сутність методів оптимізації полягає в тому, щоб, виходячи з наявності певних ресурсів, вибрати такий спосіб їх використання (розподілення), при якому буде забезпечений максимум або мінімум показника, що цікавить. Необхідною умовою використання оптимального підходу до планування (принципу оптимальності) є гнучкість, альтернативність ситуацій, в умовах яких доводиться приймати планово-управлінські рішення.

Оптимальне програмування можна застосовувати лише до таких завдань, при вирішенні яких оптимальний результат досягається лише у вигляді точно сформульованих цілей і при певних обмеженнях У постановку задачі зазвичай входить деяка математично сформульована система взаємозалежних чинників, ресурси і умови, що обмежують характер їх використання.

Завдання стає вирішуваним при введенні в неї певних оцінок як для взаємозалежних чинників, так і для очікуваних результатів. Отже, оптимальність результату завдання програмування має відносний характер. Цей результат оптимальний лише з точки зору тих критеріїв, якими він оцінюється, і обмежень, введених в завдання. З усього вище слідує, що для будь-яких завдань оптимального програмування характерні три наступні моменти:

1) наявність системи взаємозалежних чинників;

2) строго певний критерій оцінки оптимальності;

3) точне формулювання умов, що обмежують використання ресурсів або чинників.

З багатьох можливих варіантів вибирається альтернативна комбінація, що відповідає всім умовам, введеним в завдання, і що забезпечує мінімальне або максимальне значення вибраного критерію оптимальності. Рішення задачі досягається вживанням певної математичної процедури, яка полягає в послідовному наближенні раціональних варіантів, відповідних вибраній комбінації чинників, до єдиного оптимального плану.

Для чисельного вирішення рівнянь з декількома невідомими та обмеженнями у Excel існує інструмент Поиск решения.

За замовчуванням інструмент не установлений, тому його потрібно встановити: вставити дистрибутивний CD-диск та оберіть у викні С е рвисàНадстро й ки… відповідний прапорець.

Якщо цільова функція та обмеження лінійні, то рішення складається у находжені множини чисел (х₁, х₂, … х_n), що мінімізують (максимізують) лінійну цільову функцію f(х₁, х₂, … х_n)= c₁х₁+c₂х₂+… +c_nх_n при m<n лінійних обмеженнях-рівняннях а_i1х₁+а_i2х₂+… +а_inх_n (де i=1,2, … m) і n лінійних обмеженнях-нерівностях х_k>=0 (де k=1, 2, … n). Інструмент Поиск решения забезпечує максимум 200 змінних клітинок х_i при пошуку рішення (n_мах=200).

Алгоритм рішення оптимізаційних задач з декількома невідомими такий:

- економічна постановка (аналіз завдання, визначення властивостей, параметрів, обмежень);

- математична постановка (математичний опис моделі, що оптимізується, – введення позначень, обмежень та побудова цільової функції);

- реалізація задачі в середовищі Microsoft Excel.

За допомогоюкнопки Параметры можна налаштувати точність, допустиме відхилення від оптимуму, метод екстраполяції (оптимізації) та інші параметри, можна завантажити або зберегти модель, що оптимізується.

Задача оптимального заселення

Економічна постановка. У курортному місті розташовані три типи готелів, кожен з яких характеризується визначеною кількістю номерів: економ, стандарт, напівлюкс, люкс. Відповідна інформація наведена у таблиці 3.3. У ній також вказано потрібну кількість номерів кожного виду.

Таблиця 3.3 – Вхідні дані задачі оптимального заселення

Номерний фонд kij
Тип номеру	Кількість номерів в одному готелі, од.	Потрібна кількість номерів, од.
Готель 1	Готель 2	Готель 3
Економ
Стандарт
Напівлюкс
Люкс
Вартість мешкання за добу (за один номер) pij
Тип номеру	Готель 1	Готель 2	Готель 3
Економ
Стандарт
Напівлюкс
Люкс

Скласти план заселення готелів з метою забезпечення максимального прибутку, якщо добовий виторг від обслуговування номерів у кожному окремому готелі має перевищувати 7000, 7000, 6000 грн відповідно.

Математична постановка. Позначимо x_ij – кількість номерів типу i (i=1,2,3,4) у j -ому готелі (j =1,2,3), що планується заселити. При цьому будуть заселені x₁₁ + x₁₂ + x₁₃ номерів економ класу, x₂₁ + x₂₂ + x₂₃ номерів класу стандарт, x₃₁ + x₃₂+x₃₃ номерів напівлюкс, x₄₁ + x₄₂ + x₄₃ номерів люкс. Виходячи з потреби у номерах різного типу отримаємо систему обмежень:

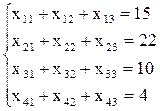(3.13)

Кількість зайнятих номерів кожного типу не може бути від’ємною, є цілою величиною та не може перевищити кількість наявних номерів. Тому

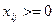
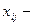цілі 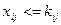(3.14)

Вартість проживання у готелі №1 складає 200 x₁₁ +400 x₂₁ +450 x₃₁+ 900 x₄₁, у готелі №2 - 300 x₁₂ +380 x₂₂ +420 x₃₂+ 1500 x₄₂, у готелі №3 - 250 x₁₃ +380 x₂₃ +430 x_33. Виходячи з умови забезпечення прибутку не менше певного рівня отримуємо систему обмежень:

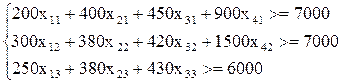(3.15)

Загальна вартість проживання складатиме:

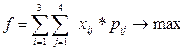(3.16)

Це і буде наша цільова функція.

Отже, математична модель задачі планування оптимального заселення: знайти такий план заселення готелів 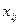, що задовольняє системам (3.13 и 3.15) та умові невід’ємності (3.14), за яких функція (3.16) приймає максимальне значення.

Реалізація задачі в середовищі Microsoft Excel. Побудуємо на листі Microsoft Excel початкову таблицю, як показано на рис. 3.38.

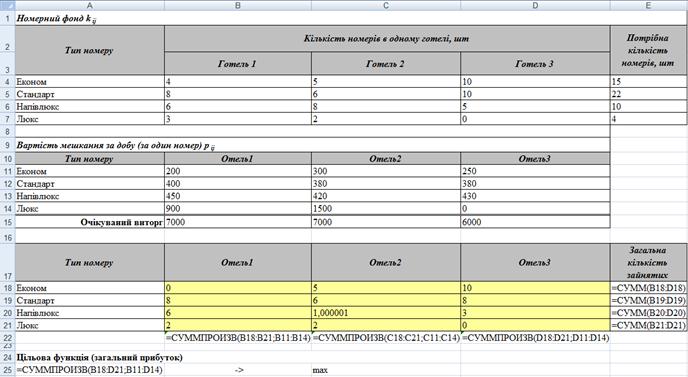
Рисунок 3.38 – Зразок заповнення початкової таблиці

У клітинках B22:D22 сформуємо задані обмеження за допомогою математичної функції СУММПРОИЗВ, аргументами якої виступають масиви даних, що містять інформацію про вартість проживання у кожному номері готелю та змінні, що відповідають за план заселення.

У клітинках E18:E21 за допомогою математичної функції СУММ розрахуємо загальну кількість зайнятих номерів за кожним типом.

У клітинці А25 побудуємо цільову функцію за допомогою функції СУММПРОИЗВ, аргументами якої є масиви відповідних даних про вартість проживання і змінні, що відповідають плану заселення.

Для вирішення поставленої задачі скористаємось надбудовою «Поиск решения». Для цього слід виконати команду Сервис - Поиск решения і заповнити діалогове вікно як показано на рис. 3.39 і натиснути на кнопку Выполнить.

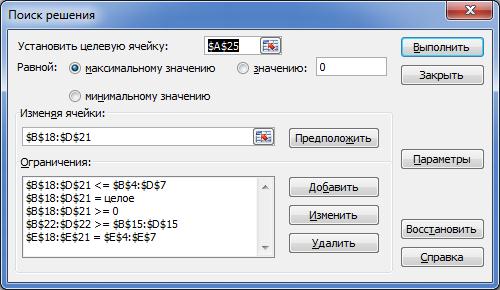
Рисунок 3.39 – Зразок заповнення діалогового вікна «Поиск решения»

В результаті виконання визначеної кількості ітерацій отримуємо такі результати (рис. 3.40): для отримання максимального добового виторгу у розмірі 21 730 грошових одиниць, забезпечення необхідною кількістю номерів різного типу, отримання заданого добового виторгу за кожним готелем слід заселити у 1-ому готелі 8 стандартних номерів, 6 напівлюксів, 2 люкса, у 2-ому готелі 5 економ номерів, 6 стандартних, один напівлюкс та 2 люкса, у 3-му готелі – 10 економ, 8 стандартних, 3 напівлюкси.

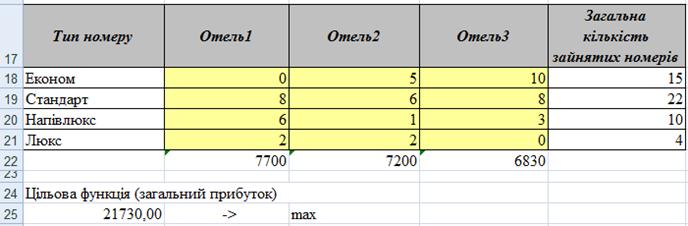
Рисунок 3.40 – Результат пошуку рішення

Задача оптимального перевезення (транспортна задача)

Економічна постановка. Існує чотири туристичні бази, які можуть вмісти певну кількість туристів і три фірми перевізники, які можуть перевезти певну кількість туристів. У таблиці 3.4 наведено витрати на перевезення одного туриста кожним перевізником до кожної бази.

Таблиця 3.4 – Вхідні дані задачі оптимального перевезення

Перевізники	Потужності перевізників	Туристичні бази та їхній попит

Скласти план перевезення таким чином, щоб загальні витрати на перевезення були мінімальними.

Математична постановка. Позначимо х_ij – кількість туристів, яких необхідно перевезти i-м перевізником до j-ої туристичної бази. План перевезення задається матрицею.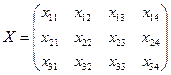

Сумарна кількість туристів, яку можуть перевезти перевізники, дорівнює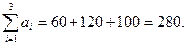

Сумарна кількість туристів, яку можуть прийняти туристичні бази, дорівнює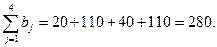

Як бачимо, обидві суми співпадають, отже, задача закритого типу, тобто, попит туристичних баз дорівнює можливостям фірм перевізників:

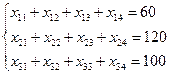(3.17)

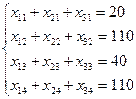(3.18)

Кількість туристів не може бути від’ємною, тому

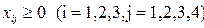(3.19)

Сумарні витрати на перевезення туристів обчислюються таким чином:

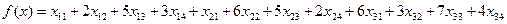(3.20)

Отже, математична модель задачі планування оптимального перевезення: знайти такий план перевезення 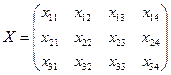, що задовольняє системам (3.17), (3.18) і умові (3.19), при якому цільова функція (3.20) приймає мінімальне значення:

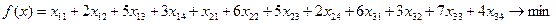
Реалізація задачі в середовищі Microsoft Excel. Побудуємо на листі Microsoft Excel початкову таблицю, як показано на рис. 3.41.

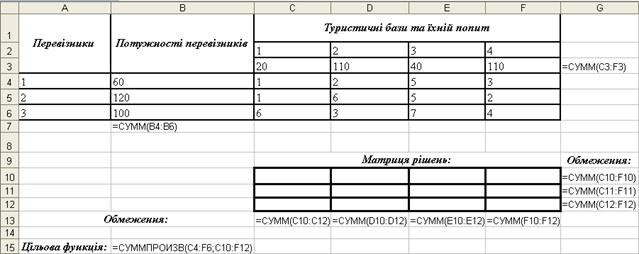
Рисунок 3.41 – Зразок заповнення початкової таблиці

В клітинках G10:G12 та С13:F13 сформуємо задані обмеження за допомогою математичної функції СУММ, аргументами якої виступають масиви відповідних даних про кількість туристів, яких необхідно перевезти.

В клітинці В15 побудуємо цільову функцію за допомогою СУММПРОИЗВ, аргументами якої виступають масиви відповідних даних про вартість перевезення і змінні, що відповідають плану перевезення.

Для вирішення поставленої задачі скористаємось надбудовою «Поиск решения». Для цього слід виконати команду Сервис - Поиск решения і заповнити діалогове вікно як показано на рис. 3.42 і натиснути на кнопку Выполнить.

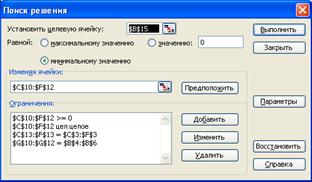
Рисунок 3.42 – Зразок заповнення діалогового вікна «Поиск решения»

В результаті виконання визначеної кількості ітерацій отримуємо такі результати (рис. 3.43): для отримання мінімальних витрат на перевезення – 760 грошових одиниць та забезпечення необхідною кількістю туристів туристичні бази необхідно виконати план перевезення, що отримано в діапазоні С10:F12.

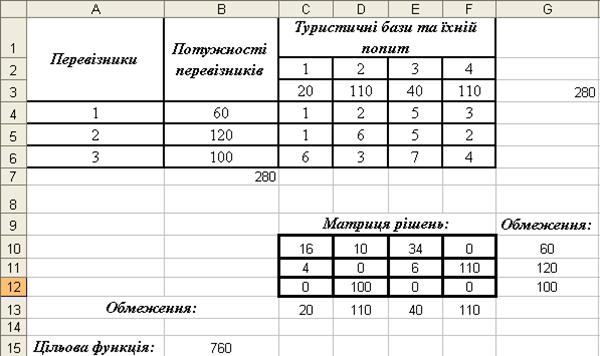
Рисунок 3.43 - Результат пошуку рішення

У склад Excel входить файл з прикладами використання інструменту Поиск решения Solvsamp.xls (розташований звичайно у папці Program Files\Microsoft Office\Office\Samples). Кожний лист містить приклади — "Структура производства", "Транспортная задача", "График занятости", "Управление капиталом", "Портфель ценных бумаг" і "Проектирование цепи", де підібрані цільова та змінні клітинки, а також обмеження.

Контрольні питання

1. Чим відрізняються відносні та абсолютні адресації Excel? Як зробити адрес клітинки абсолютною?

2. Як виконати сортування даних?

3. Для чого призначена функція СЦЕПИТЬ?

4. Як і для чого використовують автофільтр та проміжні підсумки?

5. Що дозволяє виконати інструмент Умовне форматування?

6. За допомогою якого інструменту здійснюється Автоматичне заповнення значень.

7. Які стандартні функції можуть використовуватися для прогнозування даних.

8. За яким принципом вибирається тип лінії тренда, що характеризує загальну тенденцію явища?

9. Які основні компоненти часових рядів ви знаєте?

10. На що вказує коефіцієнт детерміації?

11. Як розраховується сезонна компонента?

12. За допомогою якого показника визначається точність моделей?

13. Що відображає довірчий інтервал?

14. У чому полягає сутність методів оптимізації?

15. Для яких завдань можна застосовувати оптимальне програмування?

16. За допомогою якого інструменту Excel здійснюється чисельне вирішення рівнянь з декількома невідомими та обмеженнями?

17. Наведіть алгоритм рішення оптимізаційних задач з декількома невідомими.

18. Для чого призначена функція СУММПРОИЗВ і що може виступати її аргументами?

19. У чому полягає економічна сутність задачі оптимального планування?

20. У чому полягає економічна сутність транспортної задачі?

Практичні завдання

Дата добавления: 2014-10-15