Количество информации

Может вызвать замешательство вопрос, - в каком из двух сообщений содержится больше информации, например: «Выпал орел» (при бросании монеты), или «Выпала тройка» (при бросании игрального кубика). На этот вопрос дает ответ теория информации. Теория информации позволяет дать количественную оценку информации. Это делает возможным сравнить информативность передаваемых сообщений о том или ином состоянии системы (источнике сообщений).

Передача информации возможна, если система (источник сообщений) находится в нескольких состояниях (случайных). Рассмотрим простейший случай, когда число возможных состояний системы n и все возможные состояния равновероятны. В этом случае для количественной оценки информации, содержащейся в сообщении о состоянии системы, используется формула, предложенная в 1928 году американским инженером Хартли [24].

I(Xi) = Log _k [1/р(Xi)] = Log _k n, где:

I(Xi} – количество информации в сообщении Xi;

k – основание логарифма;

n – число возможных состояний системы;

р(Xi) = 1/n – вероятность появления равновероятного сообщения Xi.

В теории информации используются двоичные логарифмы, т.е. k = 2. В этом случае, согласно формуле Хартли, единица количества информации будет содержаться в сообщении о состоянии системы, находящейся в одной из двух возможных равновероятных состояниях. В этом случае р(Xi) = ½,

I(Xi) = Log 2 = 1.

Эта единица получила название бит и используется для оценки количества информации. Если подкинуть монету и сообщить: «Выпал орел», то это сообщение будет содержать 1 бит информации. Вероятность выпадения орла и решки одинакова и равна ½.

Если подкинуть игральный кубик и сообщить, что выпала, например, «тройка», то в этом сообщении будет содержаться следующее количество информации:

р(Xi) = ¹/_6, I(Xi) = Log 6 =2,585 бит.

Вышеприведенная формула показывает, что чем меньше вероятность появления сообщения, тем большее количество информации оно содержит. На рис. 1.1 приведен примерный вид зависимости количества информации содержащегося в сообщении от вероятности появления этого сообщения.

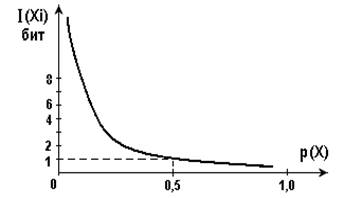Рис.1.1. Зависимость количества информации от вероятности появлении сообщения.

При вероятности появления сообщения равном единице, количество информации равно нулю. Таким образом, достоверное сообщение не несёт информации.

Дата добавления: 2014-10-15