Одноёмкостный объект с самовыравниванием

Типовые объекты регулирования и их свойства.

Объекты автоматического регулирования характеризуются некоторыми переменными и постоянными параметрами. Через объект непрерывно поступает вещество или энергия. В установившемся режиме приток вещества или энергии в объект равен расходу, в следствие чего регулируемая величина (температура, давление и т.д.) не изменяется. Если объект испытывает возмущающее воздействие, т.е. воздействие, нарушающее равенство притока и расхода вещества, регулируемая величина изменяется. Характер этого изменения зависит как от возмущающего воздействия так и от свойств объекта.

Количество вещества или энергии, содержащееся в объекте в данный момент времени называют ёмкостью объекта регулирования.

Ёмкость отражает способность объекта накапливать вещество или энергию и характеризует его инерционность.

Объект может обладать ёмкостью только при наличии в нём сопротивления выходу вещества или энергии.

Различают одноёмкостные и многоёмкостные объекты.

При всём многообразии ОР их так же, как и любые элементы САР можно классифицировать по динамическим свойствам и отнести либо к типовому динамическому звену, либо к комбинации таких звеньев.

Различают объекты с самовыравниванием (саморегулированием) и без самовыравнивания.

Самовыравнивание характеризует свойство ОР самостоятельно приходить к новому установившемуся режиму при ограниченном возмущающем воздействии.

Перечисленные ОР могут иметь запаздывания. Рассмотрим свойства ОР.

Примером такого ОР может служить бассейн, показанный на рисунке 10.1.

Рисунок 10.1 – Одноёмкостный объект с самовыравниванием

В бассейн непрерывно подаётся вода в количестве м3/мин, и также непрерывно отбирается для производственных нужд в количестве м3/мин. Выходная (регулируемая) величина – уровень Н воды, который необходимо поддерживать в заданных пределах.

Установившийся режим:

Приток воды = Расходу

Н = Н(0) = const

Нанесём объекту возмущение, резко уменьшив расход воды клапаном 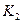на величину.

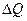Расход воды станет равным:

Поскольку расход стал меньше притока, уровень воды в бассейне начнёт возрастать (рис10.1в). Увеличение столба жидкости ведёт к повышению давления на выходе из бассейна, поэтому расход Q2 будет увеличиваться по мере роста уровня.

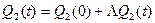
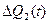– зависит от Н(t).

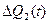– приращение расхода (рис. 10.1.б).

Когда расход достигнет значения притока , изменение выходной величины Н закончится и наступит новый установившийся режим, которому соответствует Н(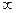) (рис.10.1.в).

Для малых изменений уровня можно приближённо считать, что изменение расхода воды пропорционально изменению уровня:

,

Где – постоянный коэффициент (м2/мин), зависящий от свойств объекта.

= Н(t) – Н(0) – приращение уровня.

Получим дифференциальное уравнение ОР, используя уравнение материального баланса (закон сохранения вещества и энергии).

Закон сохранения вещества (или энергии):

Накопление вещества = приток – расход.

За время Δt объем воды в бассейне возрастет на величину:

(1)

S – площадь поперечного сечения бассейна. По графику (рис 10.1.б) видно что:

Q₁₀ – Q₂(t) = ΔQ – ΔQ₂(t)

То есть

При малых приращениях и учитывая, что :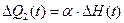

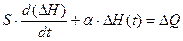(2)

Все члены этого уравнения имеют определенную размерность. Для анализа динамических свойств ОР перейдем к уравнению в относительных единицах. Для этого введем следующие обозначения:

,

,

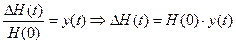Здесь в качестве базовых величин приняты значения при установившемся режиме Н(0) и Q₂₀. Тогда уравнение (2) примет вид:

,

Поделим обе части на Q₂₀

(3)

Нетрудно видеть, что коэффициент при производной:

()

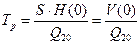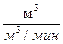равен времени, необходимому для полного опустошения бассейна от номинального уровня Н(0) с постоянной скоростью, при значении расхода Q₂₀ и при отсутствии поступающей жидкости в бассейн (Q₁ = 0). Аналогично молжно интерпретировать время заполнения бассейна (при Q₂ = 0).

В связи с этим величина Тр называется временем разгона объекта. Очевидно, что Тр зависит от Н(0) и Q₁₀.

В уравнении (3) коэффициент при переменной y(t) безразмерный. Он называется коэффициентом самовыравнивания объекта.

.

Объект лишен самовыравнивания, когда ρ = 0, если при неизменном значении расхода (ΔQ1(t) = 0), уровень воды изменяется ΔН(t)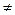0.

Учитывая введенные величины, уравнение (3) примет вид:

.

Для перехода к стандартной форме записи, поделим все члены уравнения на ρ:

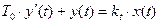(4)

где 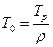- постоянная времени объекта;

- коэффициент передачи объекта по возмущающему воздействию.

Уравнение (4) соответствует дифференциальному уравнению апериодического звена 1-го порядка. Поэтому рассматриваемый объект обладает динамическими характеристиками этого звена.

; .

Дата добавления: 2014-10-15