Методы определения поверхностного натяжения

Поверхностное натяжение является важной характеристикой поверхности раздела фаз и поверхностных явлений.

Наиболее часто для определения поверхностного натяжения применяют следующие методы: наибольшего давления, сталагмометрический, отрыва кольца и уравновешивания пластинки (метод Вильгельми)

Метод наибольшего давления основан на продавливании пузырька газа или воздуха под воздействием внешнею давления р через калиброванный капилляр радиусом r₀(рис. 5.7, a). С увеличением давления пузырек растет, а радиус кривизны его поверхности R превышает радиус капилляра (положение 1: R > r₀). Дальнейшее увеличение объема пузырька будет происходить до тех пор, пока внутреннее давление достигнет своего максимального значения [см. формулу (2.23)]; радиус кривизны при этом будет минимальным, т.е. R = r₀(положение 2). В этот момент пузырек потеряет устойчивость: при увеличении его объема он отрывается от капилляра. Если в момент отрыва пузырька измерить давление р, то поверхностное натяжение согласно формуле (2.23) можно выразить следующим образом:

р = 2σ/r₀; σ = рr₀/2. (5.14)

Для того чтобы не измерять радиус капилляра, можно определить р для жидкости, поверхностное натяжение которой известно. В качестве эталонной жидкости часто используют воду. Тогда вместо формулы (5.14) можно записать

р_Н2О= 2σ_Н2О/r₀. (5.15)

Исключив в уравнениях (5.14) и (5.15) радиус капилляра, получим выражение для определения поверхностного натяжения:

σ = σ_Н2О(р/р_Н2О). (5.16)

Зная σ_Н2Ои измерив р_Н2Ои р, можно по формуле (5.16) легко рассчитать поверхностное натяжение исследуемой жидкости или раствора.

В сталагмометрическом методе определяют вес капли, которая отрывается от капилляра (см. рис 5.7, б) под действием силы тяжести или в результате выдавливания микрошприцом. Приближенно считают, что при отрыве вес капли Ркуравновешивается силой, равной поверхностному натяжению, умноженному на длину окружности капилляра радиусом r₀, т.е.

Рк= 2πr₀σ/k, (5.17)

где k — поправочный коэффициент, учитывающий, что отрыв капель происходит по радиусу шейки капли, который меньше радиуса самой капли.

Экспериментально определяют вес капель и при помощи разработанных таблиц с учетом формулы (5.17) находят поверхностное натяжение.

При измерении поверхностного натяжения методом наибольшего давления и сталагмометрическим методом пузырек и капля формируются сравнительно быстро за время, недостаточное для образования адсорбционного слоя растворенных молекул ПАВ, особенно, если они имеют сравнительно большую молекулярную массу В этих условиях не успевает установиться равновесное поверхностное натяжение. Для подобных растворов рекомендуется увеличивать время формирования пузырька или капли до тех пор, пока давление или число капель станут постоянными.

В методе отрыва кольца (см. рис.5.7, в) измеряют силу F, которой противодействует поверхностное натяжение жидкости, смачивающей периметр поверхности кольца:

F = 4πr_кσ/k; σ = (F/4πr_к)k. (5.18)

Коэффициент k является поправочным, он учитывает что поднимающийся при отрыве кольца столб жидкости не имеет формы правильного полого цилиндра.

В методе уравновешивания пластинки (или методе Вильгельми) определяют силу F, необходимую для извлечения из жидкости погруженную в нее тонкую пластинку шириной h (см. рис. 5.7, г):

F = 2σh; σ = F/(2h). (5.19)

Перечисленные выше методы определения поверхностного натяжения доступны, но имеют один общий недостаток — низкую точность измерений. Более точным является метод капиллярного поднятия (см. параграф 18.3) в том случае, если капилляр хорошо смачивается водой, а его диаметр не изменяется по высоте, что в лабораторных условиях не всегда соблюдается. Причем чем меньше радиус капилляров, тем точнее результаты измерений поверхностного натяжения.

Кроме перечисленных доступных и широко используемых методов определения поверхностного натяжения существуют и другие методы: сидячей капли, вращающейся капли и др.

Упражнения

1. При какой концентрации поверхностное натяжение валериановой кислоты будет равно 52,1 мДж/м², если при 273 К коэффициенты уравнения Шишковского а = 14,72∙10^—3, b = 10,4?

Воспользуемся формулой (5.2):

Δσ = σ₀— σ = 2,3a lg(1+bc);

lg(1 + bc) 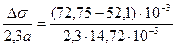= 0,61, 1+bc = 4,07,

c == 0,295 кмоль/м³.

2. При 293 К и концентрации пропионовой кислоты 0,1 кмоль/м³коэффициенты уравнения Шишковского а = 12,8∙ 10^—3, b = 7,16. Определить адсорбцию и поверхностную активность.

Из уравнений (4.34) и (5.7) находим

= 2,19∙10^—3кмоль/м²,

или 2,19 моль/м².

Согласно уравнению (4.18)

5,33 ∙ 10^—2Дж ∙ м/кмоль, или 53,3 мДж ∙м/кмоль.

Дата добавления: 2014-10-15