В зоне проводимости

Равновесная концентрация электронов

В состоянии равновесия

Носители заряда в полупроводнике

Рассмотрим, каким образом может быть рассчитана равновесная концентрация электронов в зоне проводимости. Пусть N_n(E) – энергетическая плотность электронных состояний в зоне проводимости (с учетом спинов), приходящихся на единицу объема полупроводника. Согласно определению (см. п.1.1.4) произведение N_n(E)dE дает объёмную концентрацию электронных уровней с энергиями от E до E+dE. Если N_n(E)dE умножить на f_on(E,T) – равновесная вероятность заполнения электронами уровней с энергией E при температуре T, то получим концентрацию электронов в зоне проводимости, энергии которых лежат в интервале от E до E+dE. Интегрируя по всем энергиям зоны проводимости, получим выражение для полной равновесной концентрации электронов n_o в зоне проводимости

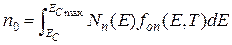. (1.2.1)

Для электронов – частиц с полуцелым спином, подчиняющихся принципу запрета Паули - f_on(E,T) есть функция распределения Ферми - Дирака

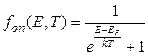, (1.2.2)

где k – постоянная Больцмана; Т – абсолютная температура; E_F – так называемая энергия Ферми (уровень Ферми). Зависимость положения уровня Ферми от температуры и уровня легирования полупроводника мы обсудим в следующем параграфе, а пока что будем считать его положение заданным.

Рассмотрим так называемые невырожденные полупроводники, у которых уровень Ферми располагается в запрещенной зоне, и при заданной температуре Т отстоит от её краев не менее чем на (2÷3)∙kT. Для уровней зоны проводимости таких полупроводников выполняется неравенство 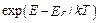>>1, поэтому для них выражение (1.2.2) для функции распределения может быть с достаточной точностью заменено более простой формулой

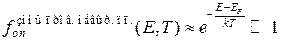. (1.2.3)

Формула (1.2.3) показывает:

1. Электроны зоны проводимости невырожденного полупроводника фактически подчиняются статистике Больцмана: уровней много, электронов мало, конфликта между ними «на почве принципа Паули» не возникает, и они ведут себя почти как классические частицы.

2. Вероятность заполнения энергетических уровней зоны проводимости невырожденного полупроводника очень быстро убывает с ростом энергии.

Последнее обстоятельство означает, что основная часть свободных электронов располагается вблизи дна зоны проводимости. Это в сою очередь позволяет:

а) использовать для всей зоны проводимости в качестве N_n(E) выражение (1.1.2)

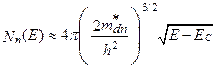, (1.2.4)

описывающее энергетическую плотность электронных уровней вблизи дна зоны проводимости, приходящихся на единицу объёма полупроводника. (Напомним, в (1.2.4) m_dn^*- эффективная масса электрона для плотности состояний, h = 6,626∙10^-34 Дж∙с – постоянная Планка);

б) устремить в (1.2.1) верхний предел интегрирования к бесконечности (E_{С max}® ∞).

В итоге для расчёта равновесной концентрации электронов в зоне проводимости невырожденного полупроводника получим общую формулу вида

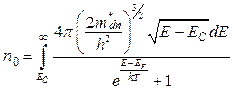. (1.2.5)

В (1.2.5) использовано точное выражение (1.2.2) для функции распределения Ферми – Дирака и приближённое выражение (1.2.4) для плотности электронных состояний в зоне проводимости. В курсе физики твёрдого тела будет показано, что для невырожденного полупроводника интегрирование в (1.2.5) приводит к выражению

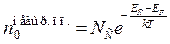. (1.2.6)

Величину N_С (см^-3) называют эффективной плотностью электронных состояний в зоне проводимости и вычисляют по формуле

N_С = =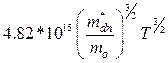

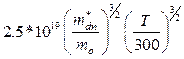= . (1.2.7)

Приведем некоторые числовые оценки: при T = 300K, m^*_dn» m_o, где m_o – масса свободного электрона, получаем N_С = 2.5∙10¹⁹ см^-3. По физическому смыслу величина N_С близка к числу уровней зоны проводимости приходящихся на 1 см³ в интервале энергий от E_С до E_С + kT. Согласно (1.2.6) в невырожденном полупроводнике при T = 300K n_o << N_С.

Дата добавления: 2014-10-15