Высокие температуры

При достаточно высоких температурах концентрация дырок может стать сравнимой с концентрацией электронов. В этом случае следует отказаться от приближенного уравнения электронейтральности в форме (1.3.9) и рассмотреть основное уравнение (1.3.8):

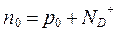. (1)

При высоких температурах:

• практически вся примесь ионизована, и можно полагать

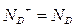(2)

• концентрация дырок подчиняется формуле (1.3.11) для невырожденного полупроводника

. (3)

С учетом (2) и (3) уравнение (1) принимает вид:

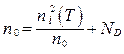; (4)

или

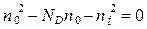. (5)

Решая (5) относительно 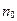и оставляя только положительный корень, получаем:

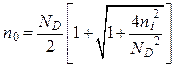. (1.3.18)

Отрицательный корень уравнения (5) отброшен, поскольку 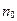- величина положительная. Зная концентрацию электронов, по формуле (1.3.1) найдём положение уровня Ферми:

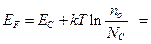
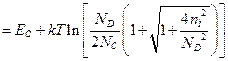(1.3.19)

Рассмотрим два предельных случая.

1). Если <<1, то согласно (1.3.19) , что совпадает с (1.3.15). При этом согласно (1.3.18) n₀ = N_D, что совпадает c (1.3.16), и согласно (1.3.11)

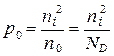, (1.3.20)

т.е. выводы, следующие из (1.3.18) и (1.3.19), находятся в полном согласии с ранее полученными результатами для области истощения примеси.

2). Если 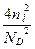>>1, то согласно (1.3.19)

. (6)

Подставив в (6) выражение (1.2.16) для собственной концентрации свободных носителей заряда

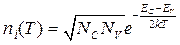, (7)

получим формулу

, (1.3.21)

совпадающую с равенством (1.3.6) для собственного полупроводника. Используя (6) или (1.3.21), по формулам (1.2.6) и (1.2.13) находим, что в области очень высоких температур 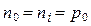, как и следовало ожидать для собственного полупроводника.

Определим температурную границу Т_i перехода от примесной проводимости к собственной условием

р₀(Т_i) = N_D. (1.3.22)

При полной ионизации доноров равновесная концентрация электронов при T = T_i согласно (1) и условию электронейтральности будет вдвое превышать концентрацию дырок

n₀(T_i) = 2p₀(T_i) = 2N_D, (1)

а произведение равновесных концентраций носителей зарядов разных знаков будет равно

n₀(T_i)∙р₀(Т_i) = 2 N_D². (2)

Согласно закону действующих масс для невырожденного полупроводника (1.2.15) для граничной температуры T_i имеем равенство

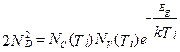, (3)

из которого получаем более удобную форму записи трансцендентного уравнения для определения условной границы перехода от примесной проводимости к собственной

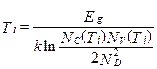. (1.3.23)

Из (1.3.23) следует:

• при фиксированном значении N_D температура перехода к собственной проводимости тем выше, чем шире запрещённая зона полупроводника;
• для данного полупроводника температура перехода к собственной проводимости возрастает при увеличении концентрации легирующей примеси (см. рис. 1.3.1).

Подводя итог рассмотрениям пункта 1.3.3 можно сказать, что положение уровня Ферми в невырожденном полупроводнике с примесью донорного типа во всем интервале температур описывается двумя выражениями: (1.3.12) и (1.3.19).

Выражение (1.3.12)

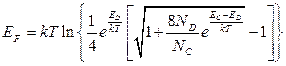
справедливо в области температур от Т = 0К до температуры истощения примеси . Выражение (1.3.19)

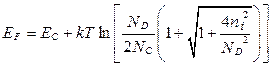
справедливо от температуры истощения примеси и выше, включая температуру 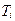перехода к собственной проводимости. В области примесной проводимости для определения положения уровня Ферми в полупроводниках с примесью донорного типа удобно пользоваться формулой (1.3.15)

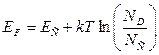
Полученные закономерности отражены схематически на рисунке 1.3.1.

Дата добавления: 2014-10-15