Легирующих примесей

Заряда от температуры и концентрации

Зависимость подвижности свободных носителей

Согласно формулам (1.5.6)

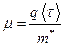. (1)

Величина W, обратная времени релаксации упорядоченного движения носителей <τ>, определяет вероятность рассеяния носителя в единицу времени

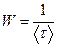. (1.5.13)

В полупроводниковых материалах существуют несколько механизмов рассеяния свободных носителей заряда:

· рассеяние на колебаниях решётки (на фононах);

· рассеяние на ионах примесей;

· рассеяние на нейтральных примесных атомах;

· рассеяние на дислокациях и границах зёрен и т.д.

Если принять, что все механизмы рассеяния независимы, то полная вероятность рассеяния носителя в единицу времени определится выражением

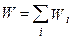, (3)

где W_i – парциальная вероятность, обусловленная i-м механизмом рассеяния. Введём в рассмотрение

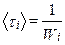(4)

- характерное время релаксации упорядоченного движения свободных носителей заряда, обусловленное i-м механизмом рассеяния, и соответствующую ему величину

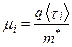(5)

- дрейфовую подвижность носителей при наличии только i-го механизма рассеяния. На основании (3) при учёте (2) и (4) можем записать

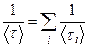. (6)

Согласно (6) результирующее время релаксации упорядоченного движения носителей оказывается меньше наименьшего из времён <τ_i>. Домножая обе части (6) на m^*/q и учитывая (1) и (5), получим соотношение, связывающее полную и парциальные подвижности свободных носителей заряда

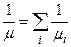. (1.5.14)

Теоретические исследования и эксперимент показывают, что в элементарных полупроводниках (Ge, Si)

1).Подвижность свободных носителей заряда при рассеянии на тепловых колебаниях решётки (на фононах) уменьшается с ростом температуры и увеличением эффективной массы носителя согласно закону

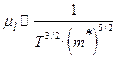. (1.5.15)

Рассеяние на фононах оказывается доминирующим механизмом рассеяния носителей при умеренных и высоких температурах.

2). Подвижность свободных носителей заряда при рассеянии на ионах примесей возрастает с ростом температуры и уменьшается с увеличением концентрации ионов примесей по закону

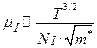, (1.5.16)

где N_I – полная концентрация различных ионов примесей. Рассеяние на ионах примесей оказывается доминирующим механизмом рассеяния носителей при низких температурах.

3).Температурная зависимость результирующей подвижности свободных носителей заряда в элементарных полупроводниках имеет вид кривой с максимумом (рис. 1.5.2)

Рис.1.5.2.Зависимость дрейфовой подвижности носителей заряда от температуры в элементарных полупроводниках (схематически)

Зависимость дрейфовой подвижности свободных носителей заряда в слабых электрических полях от температуры и концентрации легирующих примесей в полупроводниковом кремнии можно аппроксимировать выражениями /1, с.56/

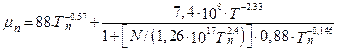, (1.5.17)

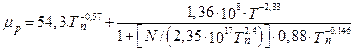, (1.5.18)

где Т – абсолютная температура; Т_n = Т/300; N – суммарная концентрация легирующих примесей в кремнии. Формулы (1.5.17) и (1.5.18) пригодны при концентрациях примесей N < 10²⁰ см^-3 и для температур в области от 250 до 500К. Подвижность электронов и дырок в слабых электрических полях в кремнии при Т = 300К в зависимости от суммарной концентрации электрически активных примесей представлена на рис. 1.5.3 /1, с. 54/

Рис.1.5.3. Подвижность и коэффициент диффузии свободных носителей заряда в кремнии при Т = 300К в зависимости от суммарной концентрации примесей

Из рис. 1.5.3 следует, что при N 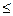10¹⁵ см^-3 подвижность носителей при Т = 300К практически перестаёт зависеть от содержания примесей в материале. При N > 10¹⁷ дрейфовая подвижность значительно ниже, чем в чистом кремнии. Следует подчеркнуть, что в полупроводниках, содержащих как доноры, так и акцепторы, в области примесной проводимости:

· концентрация основных носителей определяется модулем разности │N_D – N_A│;

• подвижность носителей зависит от суммарной концентрации N ионов доноров и акцепторов (N = N_D+N_A).

Поэтому подвижность носителей в частично компенсированном полупроводнике может быть заметно меньше, чем в полупроводнике с одним типом примеси и имеющем такую же концентрацию свободных носителей заряда, что и частично компенсированный полупроводник.

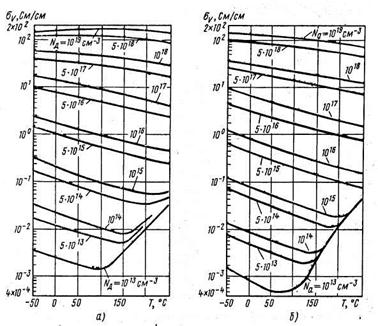
Обратимся вновь к выражению (1.5.11) для удельной проводимости полупроводника и подчеркнём, что её температурная зависимость при заданном уровне легирования определяется одновременным изменением с температурой как концентрации свободных носителей заряда, так и их подвижности. На рис. 1.5.4 показана температурная зависимость удельной проводимости кремния с разным уровнем легирования /2, с.91/

Рис.1.5.4. Температурная зависимость удельной проводимости кремния при разном уровне легирования примесью одного типа: а – кремний n-типа; б – кремний р-тпа

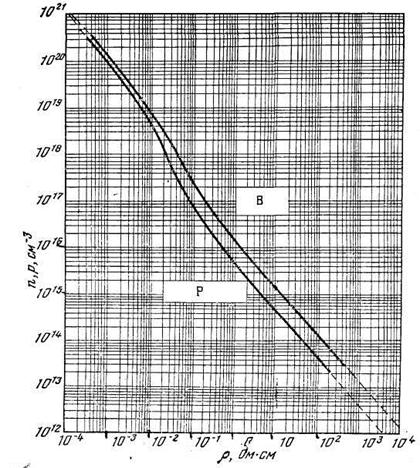
На рис 1.5.5 показана зависимость удельного сопротивления кремния при Т = 296 К от уровня легирования /1, с 51/

Рис. 1.5.5. Связь концентрации легирующей примеси с удельным сопротивлением при Т = 296К для кремния, легированного фосфором или бором

Дата добавления: 2014-10-15